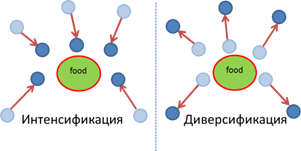
Алгоритм, основанный на поведении косяка рыб
С середины прошлого века велись исследования по симуляции биологических механизмов природы, в частности, связанные с процессом эволюции. Лишь только к 80-м годам начались практические испытания этих методов в связи с возникшей необходимостью в эффективных способах оптимизации n-арных функций, имеющих высокую вычислительную сложность, многоэкстремальность и т.д. Говоря о терминологии, стоит упомянуть, что данные алгоритмы относятся к классу стохастических поисковых. Во многих источниках также можно встретить такие определения, как поведенческий, интеллектуальный, метаэвристический или популяционный. Будем и мы последний термин использовать для классификации нашего алгоритма. Вообще говоря, данный алгоритм можно определить более точно, используя следующую схему.
Популяционные алгоритмы разделяются на следующие категории:
· эволюционные алгоритмы, включая те самые генетические;
· алгоритмы, вдохновленные живой природой (например, алгоритм оптимизации роем светлячков, кукушкин поиск и т.п.);
· алгоритмы, вдохновленные неживой природой (например, алгоритм гравитационного поиска);
· алгоритмы, основанные на поведении человеческого общества (например, алгоритм эволюции разума);
· прочие алгоритмы.
Данный алгоритм предложили в 2008 году Фило (B. Filho) и Нето (L. Neto). Как и во всех популяционных алгоритмах, в качестве входных параметров задаются: функция приспособленности (функция, для которой необходимо найти экстремумы), область исследования этой функции и параметры работы алгоритма (о них чуть позже). В текущем алгоритме FSS (Fish School Search) область поиска представляет собой аквариум, в котором плавают агенты (рыбы). Как известно, в условиях поиска пищи рыбы плавают косяком, поэтому в нашем случае конечной целью является смещение всех агентов в область экстремума функции. В общем случае схема работы алгоритма следующая:
1. Инициализация популяции (равномерное распределение рыб в аквариуме).
2. Миграция агентов к источнику пищи (аналогия: чем больший шаг агенты совершили в направлении области экстремума функции, тем больше еды они получили).
3. Завершение поиска.
Стадия «Миграция агентов» выполняется поитерационно, и в каждой из итераций выполняются операторы двух групп:
1. Операторы плавания, обеспечивающие миграцию агентов в пределах аквариума.
2. Операторы кормления, фиксирующие успех исследования тех или иных областей аквариума.
Все нижеследующие пояснения работы алгоритма рассчитаны на то, что решается задача условной максимизации функции, однако это не должно вызывать сомнений по поводу неработоспособности данного метода при поиске минимальных значений функции.
1. Итак, как уже было сказано, первым делом проводится инициализация всей популяции: случайный выбор позиции агента в пределах аквариума (swimStatePos[0]) и установка веса, равного половине от максимального (weight=weightScale/2) для всех рыб.
2. Далее начинается основной цикл алгоритма, который характеризует стадию «Миграция агентов к источнику пищи». В качестве критерия остановки в нашем случае используется величина «Количество итераций» (iterationCount).
3. Затем наступает индивидуальная стадия плавания агентов. Она характеризуется тем, что все рыбы в некоторой области вокруг себя (individStep) пытаются найти лучшее значение функции. swimStatePos[1]=swimStatePos[0]+rand(-1;1)*individStep. Если им это удается, то этот шаг фиксируется. В противном случае if(f(swimStatePos[1])<f(swimStatePos[0]|(!swimStatePos[0].IsInRegion)) считаем, что этого перемещения не было.
4. Теперь необходимо закрепить успех в индивидуальной стадии плавания. Для этого используется характеристика «Вес». Она равняется изменению функции приспособленности для данного агента до и после индивидуальной стадии, нормированного максимальным изменением функции среди популяции weight+= 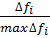 . Вообще говоря, это является отличительной особенностью данного алгоритма, так как нам не надо запоминать лучших агентов на предыдущих итерациях.
. Вообще говоря, это является отличительной особенностью данного алгоритма, так как нам не надо запоминать лучших агентов на предыдущих итерациях.
5. После этого рыбы совершают следующую стадию плавания — инстинктивно-коллективную. Для всего косяка рыб высчитывается величина «Общий шаг миграции»:
m= 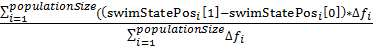
Смысл ее следующий: на каждого агента влияет вся популяция в целом, при этом влияние отдельного агента пропорционально его успехам в индивидуальной стадии плавания. Затем вся популяция смещается на подсчитанную величину m: swimStatePos[2]=swimStatePos[1]+m.
6. Перед следующей операцией плавания необходимо выполнить промежуточные действия, а именно: подсчитать центр тяжести всего косяка:
barycentre= 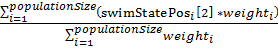
7. Мы, а точнее, рыбы, перешли к последней стадии плавания: коллективно-волевой. Здесь необходимо узнать, как изменился вес популяции по сравнению с предыдущей итерацией. Если он увеличился, значит популяция приблизилась к области максимума функции, поэтому необходимо сузить круг его поиска, тем самым проявляются интенсификационные свойства. И наоборот: если вес косяка уменьшился, значит агенты ищут максимум не в том месте, поэтому необходимо изменить направление траектории и проявить диверсификационные свойства.