Распределение Вейбулла
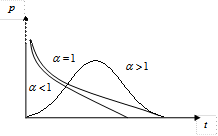
Закон Вейбулла представляет собой двухпараметрическое распределение. Этот закон является универсальным, так как при соответствующих значениях параметров превращается в нормальное, экспоненциальное и другие виды распределений (рис. 1.13).
Показатели надежности этого распределения определяются:
- плотность вероятности отказов
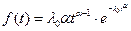 ; (1.23)
; (1.23)
- вероятность безотказной работы
 ; (1.24)
; (1.24)
- интенсивность отказов
 . (1.25)
. (1.25)
В выражениях (1.23) - (1.24)  и
и  – параметры закона распределения. Параметр
– параметры закона распределения. Параметр  определяет масштаб, при его изменении кривая распределения сжимается или растягивается. При
определяет масштаб, при его изменении кривая распределения сжимается или растягивается. При 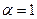 функция распределения Вейбулла совпадает с экспоненциальным распределением; при
функция распределения Вейбулла совпадает с экспоненциальным распределением; при 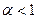 интенсивность отказов будет монотонно убывающей функцией; при
интенсивность отказов будет монотонно убывающей функцией; при 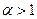 – монотонно возрастающей (см. рис. 1.13). Это обстоятельство дает возможность подбирать для опытных данных наиболее подходящие параметры
– монотонно возрастающей (см. рис. 1.13). Это обстоятельство дает возможность подбирать для опытных данных наиболее подходящие параметры  и
и  , с тем, чтобы уравнение функции распределения наилучшим образом совпадало с опытными данными.
, с тем, чтобы уравнение функции распределения наилучшим образом совпадало с опытными данными.
Средняя наработка до первого отказа определится из следующего выражения:
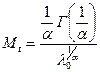 , (1.26)
, (1.26)
где 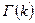 – гамма-функция,
– гамма-функция, 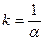 .
.
 а) а) | 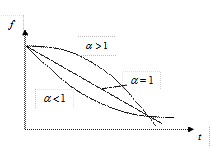 б) б) | 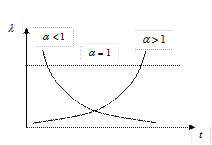 в) в) |
Рисунок 1.13 – Типичные зависимости характеристик надежности
для распределения Вейбулла
