Приведите по 1 примеру истинных и ложных высказываний из математики, биологии, истории, информатики, литературы
Практическая работа №7
Тема:Логические основы построения компьютерной техники. Основные логические операции
Цель:научиться приводить примеры истинных и ложных высказываний, выполнять операции над высказываниями, составлять таблицы истинности.
Пособия и оборудование: методические указания по выполнению практической работы.
Ход работы:
- Выполнить задания практической части
- Ответить на контрольные вопросы
- Выполнить отчет по проделанной работе. Отчет должен содержать: тему, цель, выполненные задания, ответы на контрольные вопросы, вывод о проделанной работе.
Теоретическая часть
Сумматор двоичных чисел
В целях максимального упрощения работы компьютера все многообразие математических операций в процессоре сводится к сложению двоичных чисел. Поэтому главной частью процессора являются сумматоры, которые как раз и обеспечивают такое сложение.
Полусумматор.Вспомним, что при сложении двоичных чисел в каждом разряде образуется сумма и при этом возможен перенос в старший разряд. Введем обозначения слагаемых (А, В), переноса (Р) и суммы (S). Таблица сложения одноразрядных двоичных чисел с учетом переноса в старший разряд выглядит следующим образом:
| Слагаемые | Перенос | Сумма | |
| А | В | Р | S |
Из этой таблицы сразу видно, что перенос можно реализовать с помощью операции логического умножения:
Р = А & В.
Получим теперь формулу для вычисления суммы. Значения суммы близки к результату операции логического сложения (кроме случая, когда на входы подаются две единицы, а на выходе должен получиться нуль).
Нужный результат достигается, если результат логического сложения умножить на инвертированный перенос. Таким образом, для определения суммы можно применить следующее логическое выражение:
S = (A \/ B) & ( 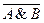 )
)
Построим таблицу истинности для данного логического выражения и убедимся в правильности нашего предложения (табл. 1.1).
Таблица 1.1. Таблица истинности логической функции 
F = (A \/ B) & ( 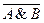 )
)
| А | В | A \/ B | A & B | 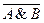 | (A \/ B) & ( 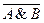 ) ) |
Теперь на основе полученных логических выражений можно построить из базовых логических элементов схему сложения одноразрядных двоичных чисел.
По логической формуле переноса легко определить, что для получения переноса необходимо использовать логический элемент «И».
Анализ логической формулы для суммы показывает, что на выходе должен стоять элемент логического умножения «И», который имеет два входа. На один из входов надо подать результат логического сложения исходных величин А и В, то есть на него должен подаваться сигнал с элемента «НЕ», а на второй вход должен поступать сигнал с элемента логического умножения «И» (рис. 4).
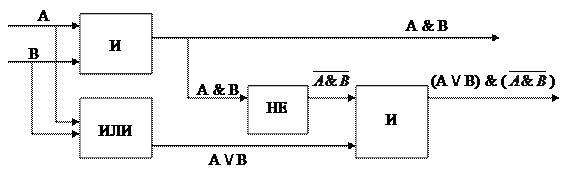
Рис. 4. Полусумматор двоичных чисел
Данная схема называется полусумматором, так как реализует суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.
Полный одноразрядный сумматор. Полный одноразрядный сумматор должен иметь три входа: А, В – слагаемые и Р0 – перенос из младшего разряда и два выхода: сумму S и перенос Р. Таблица сложения в этом случае будет иметь следующий вид:
| Слагаемые | Перенос из младшего разряда | Перенос | Сумма | |
| А | В | Р0 | Р | S |
Идея построения полного сумматора точно такая же, как и полусумматора. Из таблицы сложения видно, что перенос (логическая переменная Р) принимает значение 1 тогда, когда хотя бы две входные логические переменные одновременно принимают значение 1. таким образом, перенос реализуется путем логического сложения результатов попарного логического умножения входных переменных (А, В, Р0). Формула переноса получает следующий вид:
Р = (А & В) \/ (A & P0) \/ (B & P0).
Для получения значения суммы (логическая переменная S) необходимо результат логического сложения входных переменных (А, В, Р0) умножить на инвертированный перенос 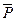 :
:
S = (A \/ B \/ P0) & 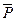
Данное логическое выражение дает правильные значения суммы во всех случаях, кроме одного, когда на все входные логические переменные принимают значение 1. Действительно:
Р = (1 & 1) \/ (1 & 1) \/ (1 & 1) = 1;
S = (1 \/ 1 \/ 1) & 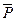 = 1 & 0 = 0.
= 1 & 0 = 0.
Для получения правильного значения суммы (для данного случая переменная S должна принимать значение 1) необходимо сложить полученное выше выражение для суммы с результатом логического умножения входных переменных (А, В, Р0). В результате логическое выражение для вычисления суммы в полном сумматоре принимает следующий вид:
S = (A \/ B \/ P0) & 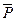 \/ (A & B & P0).
\/ (A & B & P0).
Многоразрядный сумматор. Многоразрядный сумматор процессора состоит из полных одноразрядных сумматоров. На каждый разряд ставится одноразрядный сумматор, причем выход (перенос) сумматора младшего разряда подключается ко входу сумматора старшего разряда.
Триггер.
Важнейшей структурной единицей оперативной памяти компьютера, а также внутренних регистров процессора является триггер. Это устройства позволяет запоминать, хранить и считывать информацию (каждый триггер может хранить 1 бит информации).
Триггер можно построить из двух логических элементов «ИЛИ» и двух элементов «НЕ».
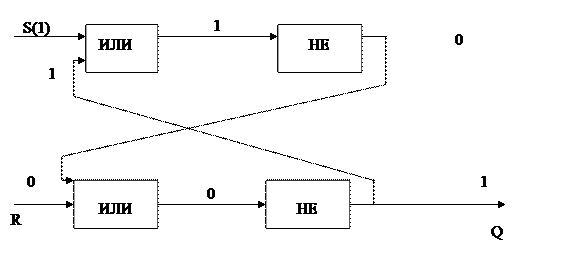
В обычном состоянии на входы триггера подан сигнал 0, и триггер хранит 0. Для записи 1 на вход S (установочный) подается сигнал 1. Последовательно рассмотрев прохождение сигнала по схеме, видим, что триггер переходит в это состояние и будет устойчиво находиться в нем и после того, как сигнал на входе S исчезнет. Триггер запомнил 1, то есть с выхода триггер Q можно считать 1.
Для того чтобы сбросить информацию и подготовить к приему новой, подается сигнал1 на вход R (сброс), после чего триггер возвратится к исходному «нулевому» состоянию.
Практическая часть.
Приведите по 1 примеру истинных и ложных высказываний из математики, биологии, истории, информатики, литературы.
2. Из следующих предложений выбрать те, которые являются высказываниями:
2.1. Коля спросил: «Как пройти к Большому театру?»
2.2. Решение задачи – информационный процесс.
2.3. Какого цвета этот дом?
2.4. Число Х не превосходит единицы.
2.5. 4х+3.
2.6. Пейте томатный сок!
3. В приведенных предложениях вместо многоточия поставьте подходящие по смыслу слова «необходимо», «достаточно», «необходимо и достаточно». Получившиеся предложения должны быть истинными.
· Для того чтобы число делилось на 4, …, чтобы оно было четным.
· Для того чтобы число делилось на 3, …, чтобы оно делилось на 9.
· Для того чтобы число делилось на 10, … чтобы оно оканчивалось нулем.
· Чтобы произведение двух чисел равнялось нулю, …, чтобы каждое из них равнялось нулю.
· Чтобы произведение двух чисел равнялось нулю, …, чтобы хоть одно из них равнялось нулю.
4. В следующих высказываниях выделите простые, обозначив каждое из них буквой; запишите с помощью букв и знаков логических операций каждое составное высказывание:
· Число 376 четное и трехзначное
· Зимой дети катаются на коньках или на лыжах
· Неверно, что Солнце движется вокруг Земли.
· Если сейчас не солнечно, то пасмурно.
· Число 15 делится на 3 тогда и только тогда, когда сумма цифр числа 15 делится на 3.
5. Постройте отрицания следующих высказываний:
· Сегодня в театре идет опера «Евгений Онегин».
· Каждый охотник желает знать, где сидит фазан.
· Неверно, что число 3 не является делителем числа 198.
6. Пусть p=Ане нравятся уроки математики; q=Ане нравятся уроки химии. Выразите следующие формулы на обычном языке:
· p*q;
· 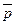 *q;
*q;
· p+q;
· 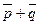 ;
;
· 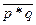 ;
;
· 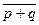 ;
;
· p 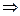 q;
q;
· 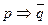 ;
;
7. Составьте таблицу истинности для следующей логической функции:
F=X & ØY Ú ØX & Y.
8. Пусть a,b,c — логические величины, которые имеют следующие значения: а = истина, b = ложь, с = истина. Нарисуйте логические схемы для следующих логических выражений и вычислите их значения:
- а и b;
- а или b;
- не а или b;
- а и b или с;
- а или b и с;
- не а или b и с;
- (а или b) и (с или b);
- не(а или b) и (с или b);;
- не (а и b и с).
9. Построить логические схемы по логическому выражению:
- х1 и (не х2 или х3);
- х1 и х2 или не х1и х3;
- х4 и (х1 и х2 и х3 или не х2 и не х3).
Контрольные вопросы
- Почему формулировка любой теоремы является высказыванием?
- Где в повседневной жизни применяется алгебра логики?
