Умножение в шестнадцатеричной системе
Пример 19. Выполните умножение чисел: A3C16 и 2E16
| A | C16 | |||
| × | ||||
| E16 | ||||
| F | ||||
| + | ||||
| D | C | 816 |
Ответ: A3C16 × 2E16 = 1D6C816.
 | 1. Заполните таблицу:
Обсудите заполненную таблицу с другими студентами группы. Внесите в нее необходимые исправления и дополнения. 2. Составьте таблицу умножения для шестнадцатеричных чисел. 3. Даны два числа: первое – в восьмеричной системе счисления, второе – в шестнадцатеричной. Найти десятичное представление их суммы. Какие способы решения этой задачи вы можете предложить? Какой способ вы считаете более рациональным? Ответ аргументируйте. |
| | Ответьте на вопросы и решите следующие задачи: 1. Сложите числа:
2. Вычтите:
3. Перемножьте числа:
4. Вычислите значения выражений: а) 2568 + 10110,12 *(608 + 1210) - 1F16; б) 1AD16 - 1001011002 : 10102 + 2178; в) 101010 + (10616 - 110111012) * 128; г) 10112 *11002 : 148 + (1000002 - 408). 5. Вычислите значение суммы 102 + 108 + 1016 в двоичной системе счисления. 6. Решите уравнение 11002·Х16=100111002.. Ответ дайте в шестнадцатеричной системе счисления. 7. Восстановите двоичные цифры в примере (на их местах в записи стоит знак *): 1*012+1**2=1*1002 8. Какие целые числа следуют за числами:
|
Модуль 4.
Кодирование информации
Тема 4.1 Представление целых чисел в компьютере
Основные понятия:
Условные обозначения:
 - задания до чтения текста |  - задания во время чтения | - задания после чтения |
| |
| | Прочитайте текст. Во время чтения делайте пометки на полях, выделяя главное. |
Целые числа могут представляться в компьютере со знаком или без знака.
Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 000000002 до 111111112 , а в двубайтовом формате — от 00000000 000000002 до 11111111 111111112.
Диапазоны значений целых чисел без знака
| Формат числа в байтах | Диапазон | |
| Запись с порядком | Обычная запись | |
| 0 ... 28–1 | 0 ... 255 | |
| 0 ... 216–1 | 0 ... 65535 |
Примеры:
а) число 7210 = 10010002 в однобайтовом формате:
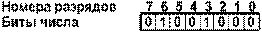
б) это же число в двубайтовом формате:
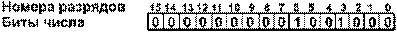
в) число 65535 в двубайтовом формате:
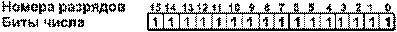
Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак “плюс” кодируется нулем, а “минус” — единицей.