Ключ на комплементарных транзисторах

Рассмотренные ранее ключи имеют существенный недостаток: в открытом состоянии ключа оба транзистора открыты, выходное напряжение логического нуля имеет не нулевое, а определенное значение, что снижает статическую помехоустойчивость. Ключ в открытом состоянии потребляет энергию. Если бы в открытом состоянии ключевого транзистора нагрузочный транзистор был закрыт, то выходное напряжение стремилось бы к нулю, и ключ не потреблял бы энергии в статических состояниях. Это удается достичь, используя ключи на комплементарных транзисторах (рис. 9.7,а).

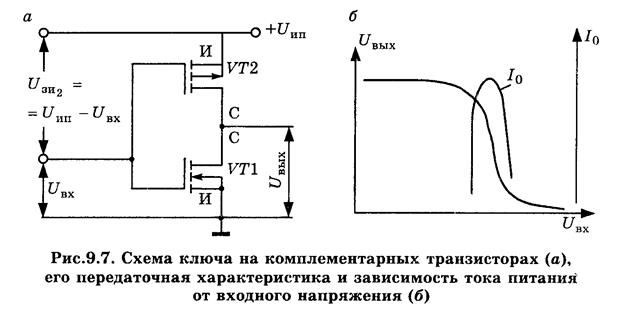
Ключ состоит из двух последовательно включенных МДП-транзисторов с каналами n– и p– типа. Транзистор VТ1 является ключевым, его исток соединен с заземленной шиной питания, а сток подсоединяется к стоку нагрузочного транзистора VТ2.

Подложка n–канального транзистора VТ1 заземлена, а p–канального подключена к положительному выводу источника питания U_ип. Затворы обоих транзисторов объединены и являются входом ключа. При этом:

1. Входное напряжение управляет не только ключевым, но и нагрузочным транзистором.

2. Управление является противофазным, напряжения на затворах транзисторов равны , .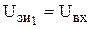

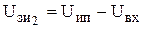При нулевом потенциале затворов транзистор VТ1 закрыт, а транзистор VТ2 открыт и работает в линейной области, так как напряжение между затвором и истоком равно U_ип. При этом ток в общей цепи определяется запертым транзистором VТ1 и составляет величину 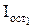. Напряжение на выходе ключа практически равно U_ип. При подаче на затворы напряжения, близкого к величине U_ип, транзистор VТ2 закрывается, а транзистор VТ1 открывается. Ток в общей цепи по-прежнему остается на уровне I_ост, хотя состояния транзисторов изменились. На выходе формируется уровень напряжения, близкий к потенциалу земли. Уровни выходных напряжений имеют почти экстремальные значения: близкое к нулю U_вых»0, близкое к напряжению источника питания U_вых»U_ип, а перепад напряжений близок к U_ип.

Важнейшей особенностью комплементарных ключей является то, что они практически не потребляют энергии в обоих состояниях. Эти состояния можно назвать "открытым" или "закрытым" только условно – по отношению к одному из транзисторов. Такие схемы расходуют энергию только при переключении из одного логического состояния в другое (рис. 9.7,б).

Микросхемы на КМДП транзисторах имеют высокое быстродействие, поскольку перезаряд емкости нагрузки как при включении, так и при выключении происходит через открытый транзистор, однако их быстродействие меньше достигнутого биполярными микросхемами. Поэтому необходимо уменьшать емкости переходов, использовать новые технологии. Применение V-образной формы затвора, пространственно замыкающей стоковые области, позволяет увеличить быстродействие по сравнению со стандартной технологией КМДП ИС в 4…5 раз.

Применение сапфировой подложки для изготовления КМДП микросхем позволило значительно уменьшить паразитные емкости переходов и увеличить быстродействие в два‑три раза.

Ключи на комплементарных МДП транзисторах имеют следующие достоинства:

– малая статическая мощность, потребляемая от источника питания;

– высокая помехоустойчивость, обусловленная большим перепадом выходных напряжений;

– широкий диапазон рабочих напряжений (3…15 В), причем для современных микросхем КМДП напряжение питания обычно составляет U_ип= 5 В, что позволяет совмещать КМДП логику с ТТЛ без промежуточных трансляторов;

– широкий диапазон рабочих температур (–55…+125 °С);

– высокое входное сопротивление (~10¹² Ом);

– простота сопряжения со слаботочными источниками входного напряжения.

Это позволяет применять КМДП микросхемы в устройствах с автономным питанием, в различных бортовых устройствах, автономных устройствах сбора и обработки данных, запоминающих устройствах без разрушения информации.

9.6. Алгебра логики и основные её законы

В схемах импульсной техники для обработки и преобразования информации используются цифровые методы. Используемые в схемах сигналы близки по форме к прямоугольным и имеют два фиксированных уровня напряжения, уровню высокого напряжения приписывается символ "1" (истинность), а уровню низкого напряжения – символ "0" (ложь). При анализе импульсных устройств используется двоичная система счисления. Математическим аппаратом анализа и синтеза цифровых систем служит алгебра логики (булева алгебра), оперирующая логическими связями и зависимостями. Основные положения алгебры логики разработал в XIX веке английский математик Джордж Буль. Значения двоичных сигналов 0 и 1 не дают количественной оценки состояния переменных или состояния их функций, поэтому эти символы нельзя рассматривать как арифметические числа. В связи с этим алгебра логики является алгеброй состояний, а не алгеброй чисел.

Функция двоичных переменных, принимающая значения "1" и "0", называется логической функцией (переключательной, функцией алгебры логики).

Элементарными логическими функциями являются: логическое сложение (дизъюнкция), логическое умножение (конъюнкция), логическое отрицание (инверсия).

Аналитические формы записи функций позволяют получить основные законы алгебры логики отдельно для операций логического умножение и сложения (И и ИЛИ).

1. Переместительный закон (закон коммутативности)

X₁X₂ = X₂X₁; X₁+X₂ = X₂+X₁.

2. Распределительный закон (закон дистрибутивности логического умножения по отношению к сложению)

(X₁+X₂)X₃ = X₁X₃+X₂X₃.

3. Сочетательный закон (закон ассоциативности)

(X₁X₂)X₃ = X₁(X₂X₃) (X₁+X₂)+X₃ = X₁+(X₂+X₃)

4. Законы повторения (тавтологии)

XX = X; X+X = X.

5. Законы поглощения

X₁(X₁+X₂) = X₁; X₁+X₁X₂=X₁.

6. Законы отрицания:

а) закон дополнительности

; ;

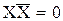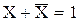б) закон дуальности ‑ правило де Моргана (инверсия суммы переменных есть произведение их инверсий)

; ;

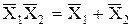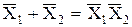в) закон двойного отрицания

.

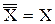7. Законы склеивания

; .

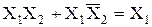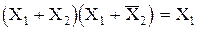8. Законы универсального множества

X×1 = X; X+1 = 1.

9. Законы нулевого множества

X×0 = 0; X+0 = X.

Логическая функция может быть выражена словесно, в алгебраической форме и переключательной таблицей (таблицей истинности).

ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (дизъюнкция, операция ИЛИ) на языке электронной схемы означает наличие напряжения на выходе схемы, при наличии на одном из входов напряжения:

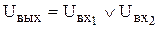или y = x₁+x₂.

Кроме символа "+", для дизъюнкции употребляется символ "Ú", т.е. y = x₁Úx₂

На рис. 9.8 представлены схемы, реализующие операцию ИЛИ. Так, если оба ключа разомкнуты (рис. 9.8,а), то напряжение на выходе равно нулю. Если положительный сигнал поступает хотя бы на вход одного из диодов (рис. 9.8,б), диод открывается, и сигнал поступает на выход схемы.

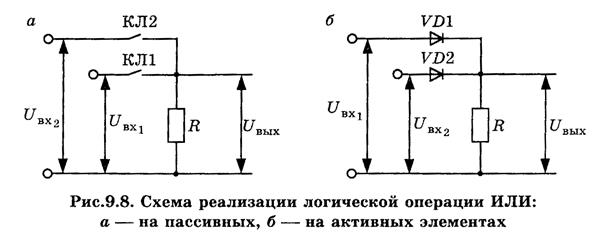
Если число входных сигналов логического элемента ИЛИ меньше числа входов, то неиспользуемые входы заземляют.

ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (конъюнкция, операция И) означает в электронной схеме наличие напряжения на выходе, при наличии всех входных сигналов.

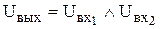или y = x₁·x₂.

Для обозначения конъюнкции часто используют символ Ù или &, т.е. y=x₁Ùx₂.

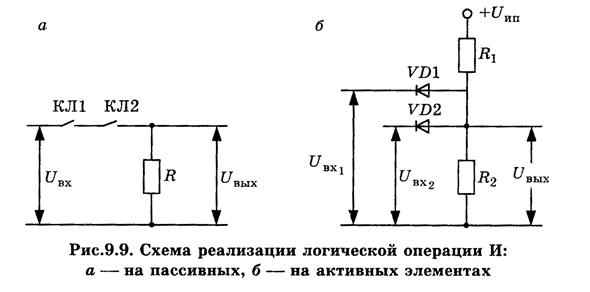
На рис. 9.9 представлены схемы, реализующие операцию И. Элемент И является схемой совпадения: сигнал "1" на выходе схемы появляется при совпадении сигналов "1" на всех его входах.

При нулевом значении сигнала хотя бы на одном из входов (рис. 9.9,б) соответствующий диод открывается. Напряжение на выходе определяется падением напряжения на открытом диоде, которое определяет значение логического нуля. Если на все входы поступает сигнал логической "1", диоды закрываются. Напряжение на выходе будет равно U_ип·R₂/(R₁+R₂), определяющее логическую "1".

На практике, если число входных сигналов логического элемента И меньше числа входов, то неиспользуемые входы подсоединяют к положительному выводу источника питания +U_ип.

ЛОГИЧЕСКОЕ ОТРИЦАНИЕ (инверсия, операция НЕ) означает, что состояние на выходе схемы противоположно состоянию на ее входе.

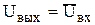и читается: (U_вых не U_вх). Эта операция реализуется с помощью транзисторного ключа.

Схемотехническая реализация многообразия цифровых ИМС основана на типовых базовых функциональных элементах, реализующих простейшие логические функции: И, ИЛИ, НЕ, ИЛИ–НЕ, И–НЕ (одноступенчатая логика). Микросхемы, выполняющие только логические функции ИЛИ–НЕ или И–НЕ, называют основными логическими элементами.

Условное обозначение логического элемента ИЛИ–НЕ и его таблица истинности представлены на рис. 9.10.

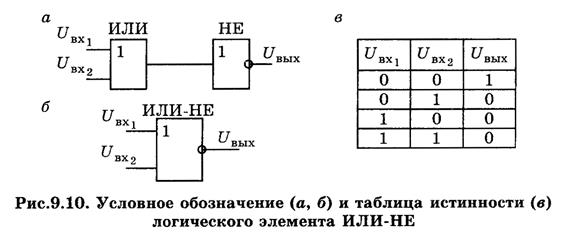
ЛОГИЧЕСКИЙ ЭЛЕМЕНТ ИЛИ–НЕ образуется путем отрицания результатов, полученных при выполнении операции ИЛИ (рис. 9.10,в). При входных сигналах, равных единице, сигнал на выходе соответствует логическому нулю, а при нулевых сигналах на всех входах сигнал на выходе равен "1" (таблица истинности рис. 9.10,в).

Алгебраическая запись операции ИЛИ–НЕ следующая:

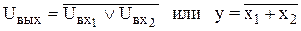
Инверсию логической суммы двух величин называют стрелкой Пирса:

.

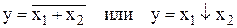ЛОГИЧЕСКИЙ ЭЛЕМЕНТ И–НЕ. Условное обозначение логического элемента И–НЕ и его таблица истинности представлены на рис. 9.11.

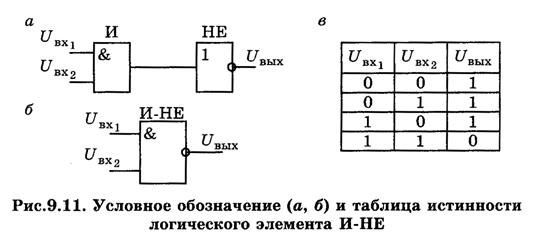
Функция И–НЕ образуется путем отрицания результата, получаемого при выполнении операции И. Число входов элемента И–НЕ определяется числом аргументов функции И–НЕ. При подаче логического нуля на один из входов на выходе образуется логическая единица. Если на всех входах действует логическая единица, то сигнал на выходе равен логическому нулю. Логическая операция И–НЕ записывается следующим образом

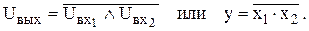
Инверсию логического произведения двух и более аргументов называют штрихом Шеффера:

.

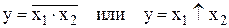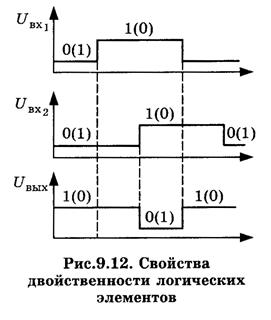Логические элементы И, ИЛИ, И–НЕ, ИЛИ–НЕ и другие обладают свойством двойственности. Оно заключается в том, что если логический элемент при положительной логике выполняет операцию, например И–НЕ, то он же при отрицательной логике выполняет операцию ИЛИ–НЕ и наоборот (рис. 9.12).

Свойство двойственности указывает на то, что любое цифровое устройство можно без изменения функциональных связей строить как на элементах И–НЕ, так и на элементах ИЛИ–НЕ. Различие состоит в том, что логические уровни напряжений на всех входах и выходах изменяются на противоположные.

Функциональные элементы, реализующие логические функции И–ИЛИ, ИЛИ–И, НЕ–И–ИЛИ, И–ИЛИ–НЕ, И–ИЛИ–И и другие, составляют двухступенчатую логику.