Свойства нормального распределения

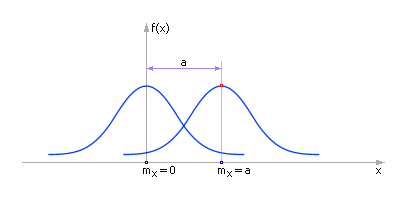
Изменение параметра нормального распределения m_x приводит к сдвигу кривой по оси x (см. рис. 25.2).

Рис. 25.2. Влияние параметра «математическое ожидание» на вид закона нормального распределения случайной величины х

Изменение параметра нормального распределения σ_x приводит к масштабированию формы по оси x (напоминаем, в любом случае всегда площадь под кривой плотности вероятности неизменна и равна 1).

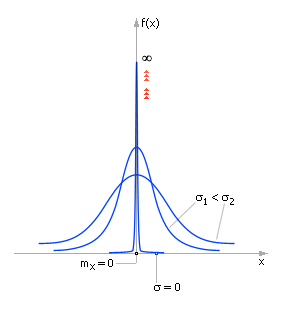
Чем более не случаен процесс, тем меньше его среднеквадратичное отклонение, тем уже и выше колокол на графике. Изменение параметра нормального распределения σ_x приводит к масштабированию формы (см. рис. 25.3) по оси x (напоминаем, в любом случае всегда площадь под кривой плотности вероятности неизменна и равна 1).

Рис. 25.3. Влияние параметра «среднеквадратичное отклонение» на вид закона нормального распределения случайной величины х

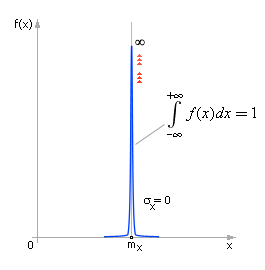
Чем более не случаен процесс, тем меньше его среднеквадратичное отклонение, тем уже и выше колокол на графике. Действительно, разброс случайности относительно математического ожидания становится все более минимальным. В пределе детерминированный процесс имеет вид, показанный на рис. 25.4.

Рис. 25.4. Вид закона нормального распределения вероятности при переходе его к детерминированному случаю в пределе (σx = 0). Случайное событие становится детерминированным: x = mx ± 0 (разброса нет)

Изучать детерминированные процессы проще. Чем больше величина σ_x, тем менее закономерно поведение изучаемого объекта, так как возможны любые значения характеризующих его параметров, разброс величин относительно средней ожидаемой увеличивается. Прогнозирование и управление поведением объекта в этом случае затрудняется.

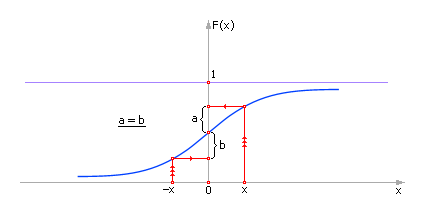
Рассмотрим вид интегральной кривой плотности распределения случайной величины, распределенной по нормального закону. Вид ее приведен на рис. 25.5. F — интегральная функция Лапласа. Смысл интегральной функции — вероятность того, что случайная величина примет значения из диапазона от –∞ до x. Например, запись F(170) = 0.5 для нашего примера означает: вероятность того, что случайно выбранный из аудитории человек будет ростом не выше 170 см, составляет 0.5 (то есть каждый второй).

Рис. 25.5. Вид интегральной функции Лапласа F(x)

Данная функция задана интегралом от плотности вероятности нормального распределения:

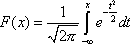
К сожалению, этот интеграл не берется в общем виде, поэтому функция Лапласа задана в виде таблицы для m_x = 0 и σ_x = 1. Поскольку функция Лапласа симметрична относительно точки (x = 0, y = 0.5) (как и функция самого нормального распределения), F(–x) = 1 – F(x), то в таблице содержится только одна из ее симметричных частей.

Если задается интервал интегрирования функции Лапласа [a; b], то:

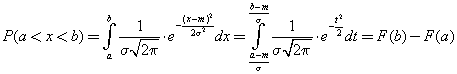
Вероятность попадания X в интервал, симметричный относительно m_x:

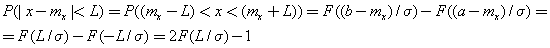
Например, для правила «трех сигм»: P(|x – m_x| < 3σ) = 2 · F(3) – 1 = 2 · 0.9987 – 1 = 0.9973 (как ранее мы и указывали). Число F(3) = 0.9987 взято из таблицы Лапласа.

Пример. Найти вероятность изготовления детали с ошибкой в ее размерах не более 15 мм, если известно, что изготовление детали с ошибкой распределено по нормальному закону m = 0 и σ = 10 мм.

P(|x| < 15) = P(–15 < x < 15) = F((15 – 0)/10) – F((–15 – 0)/10) = F(1.5) – F(–1.5) = F(1.5) – (1 –
– F(1.5)) = 2 · F(1.5) – 1 = 2 · 0.9332 – 1 = 0.8664. То есть 8664 деталей из 10000 будут иметь ошибку в размерах не более 15 мм.

ЦПТ

2.Равномерный (равновероятностный) закон распределения. Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [a, b], если ее плотность вероятности постоянна на этом отрезке и равна нулю вне его, т.е.

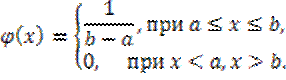
Обозначение: .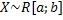

Математическое ожидание: .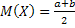

Дисперсия: .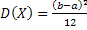

Случайная величина Х, распределенная по равномерному закону на отрезке [0, 1] называется случайным числом от 0 до 1. Она служит исходным материалом для получения случайных величин с любым законом распределения. Равномерный закон распределения встречается при анализе ошибок округления при проведении числовых расчетов, в ряде задача массового обслуживания, при статистическом моделировании наблюдений, подчиненных заданному распределению.

3.. Показательный (экспоненциальный) закон распределения. Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром λ >0, если ее плотность вероятности имеет вид:

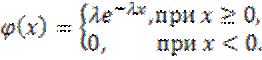
Закон Вейбулла,когда ..

Математическое ожидание: .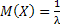

Дисперсия: .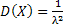

Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности.

4. Распределение Симпсона (закон треугольника).

Случайная величина распределена по треугольному распределению, если

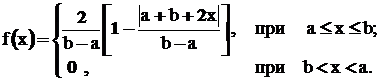
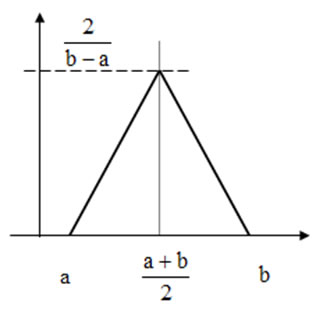
Такое распределение наблюдается тогда, когда суммируются две или вычитаются две случайные величины, которые имеют равномерный закон распределения.

; .

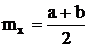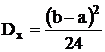5.Закон распределения Релея может быть записан в различной форме, например:

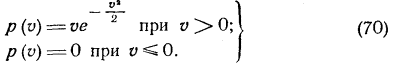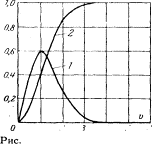
График функции (70) изображен на рис.46 (кривая 1).

1 2 3 4 5 6

Рис. 46. Распределение Релея. 1 — дифференциальный закон; 2—интегральный закон.

Закону распределения Релея подчиняются, в частности, амплитудные значения шумо­вых (флуктуационных) коле­баний (помех) в радиоприем­нике. Подробнее об этом мож­но прочесть в [Л. 6, 9 и др.]. Осциллограмма шумовых ко­лебаний показана на рис. 58. Существуют и другие физиче­ские величины, подчиняющие­ся закону Релея.

Как видно из рис. 46, плотность вероятности в начале координат равна нулю. Это оз­начает, что небольшие зна­чения амплитуды относительно мало вероятны. Очень большие значения также мало вероятны, хотя не исклю­чены, так как функция только стремится к нулю при v -> oo.

Наиболее вероятным является значение v =1. Величина v в (70) может представлять собой относительное значение амплитуды (по отношению к эффективному напряжению шумов):

v = u / s

Существуют и другие формы записи релеевского закона, например в [6] для напряжения u:

w(u) = [u/s²] exp (- u² / 2s² ) (70‘)

Интегральный закон распределения можно получить интегрируя функцию 70’.

P(u) = 1 – exp (- u² / 2s²) для u >0

2.2.8. Законы распределения дискретных результатов измерения