Дискретные случайные величины и их числовые характеристики
Дискретная случайная величина (ДСВ) может принимать конечное или бесконечное счетное число (изолированных) значений. Например, можно рассмотреть случайную величину 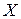 – число точек на грани игрального кубика, выпадающее при его подбрасывании [3].
– число точек на грани игрального кубика, выпадающее при его подбрасывании [3].
Законом распределения дискретной случайной величины называется соотношение между ее возможными значениями и их вероятностями (т. е. вероятностями, с которыми случайная величина принимает эти возможные значения).
Закон распределения может быть задан формулой (формулы Бернулли, Пуассона и др.), таблицей или графиком, а также функцией распределения.
Функцией распределения (интегральной функцией распределения) случайной величины 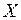 называется функция
называется функция
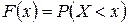 ,
,
определяющая вероятность того, что случайная величина 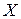 примет значение, меньшее
примет значение, меньшее 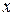 .
.
Свойства функции распределения:
а) функция распределения принимает значения только из отрезка [0,1]:
0 ≤ F(x) ≤ 1;
б) F(x) – неубывающая функция, т.е. если x2 > x1, то F(x2) > F(x1) ;
в) F(- ∞ ) = 0; F(+ ∞) = 1;
г) вероятность того, что случайная величина примет значение из
интервала 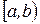 (причем
(причем 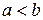 ), равна:
), равна:
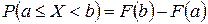 ;
;
д) F(x) непрерывна слева, т. е. F(x) = F(x – 0)
Закон распределения дискретной случайной величины может быть представлен в виде многоугольника распределения – фигуры, состоящей из точек 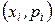 , соединенных отрезками (рис. 1.3).
, соединенных отрезками (рис. 1.3).
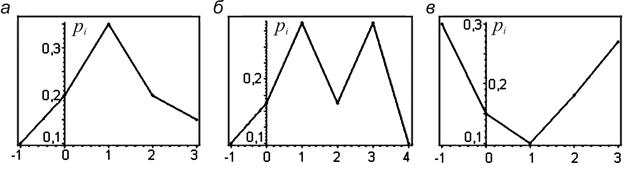
Рис. 1.3. Многоугольники уни (моно)модального (а), полимодального (б) и антимодального (в) распределений
Математическим ожиданием 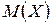 дискретной случайной величины
дискретной случайной величины 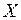 называется среднее значение данной случайной величины
называется среднее значение данной случайной величины
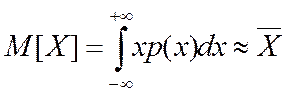
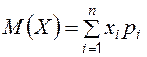 ,
,
т. е. математическое ожидание – это сумма произведений значений случайной величины 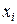 на соответствующие вероятности
на соответствующие вероятности 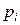 .
.
Мода 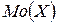 распределения – это значение СВ, имеющее наиболее вероятное значение. Если мода единственна, то распределение называется унимодальным (рис. 1.3, а), в противном случае – полимодальным (рис. 1.3, б) Если в середине диапазона изменения аргумента наблюдается минимум на графике многоугольника вероятностей, тогда распределение называется антимодальным (рис. 1.3, в).
распределения – это значение СВ, имеющее наиболее вероятное значение. Если мода единственна, то распределение называется унимодальным (рис. 1.3, а), в противном случае – полимодальным (рис. 1.3, б) Если в середине диапазона изменения аргумента наблюдается минимум на графике многоугольника вероятностей, тогда распределение называется антимодальным (рис. 1.3, в).
Медиана 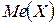 – это значение случайной величины, которое делит таблицу распределения на две части таким образом, что вероятность попадания в одну из них равна 0,5
– это значение случайной величины, которое делит таблицу распределения на две части таким образом, что вероятность попадания в одну из них равна 0,5
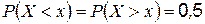 .
.
Медиана обычно не определяется для дискретной случайной величины.
Величина 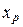 , определяемая равенством
, определяемая равенством 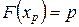 , называется квантилью порядка
, называется квантилью порядка 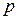 . Соответственно квантиль порядка 0,5 является медианой.
. Соответственно квантиль порядка 0,5 является медианой.
Свойства математического ожидания.
а) 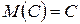 , где
, где 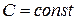 ;
;
б) 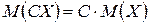 ;
;
в) 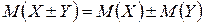 ;
;
г) если случайные величины 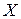 и
и 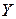 независимы, то
независимы, то 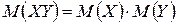 .
.
Дисперсией 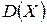 ДСВ
ДСВ 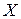 называется математическое ожидание квадрата отклонения СВ от ее математического ожидания
называется математическое ожидание квадрата отклонения СВ от ее математического ожидания
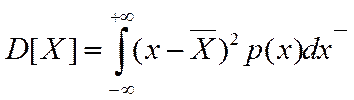
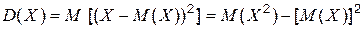 ,
,
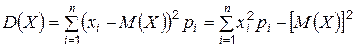 .
.
Дисперсия служит для характеристики рассеяния СВ относительно ее математического ожидания
.
Свойства дисперсии:
а) 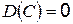 , где
, где 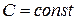 ;
;
б) 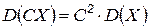 ;
;
в) 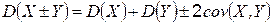 ,
,
где 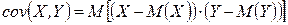 – ковариация двух случайных величин
– ковариация двух случайных величин 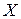 и
и 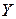 ;
;
г) если 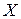 и
и 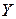 некоррелированы, то
некоррелированы, то 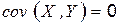 , тогда
, тогда 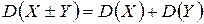 .
.
Средним квадратическим отклонением 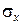 называется величина, которая имеет ту же размерность, что и СВ
называется величина, которая имеет ту же размерность, что и СВ 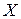 :
:
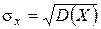 .
.
При1. гипергеометрическом законе вероятность появления 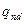 числа
числа 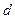 дефектных изделий в выборке с числом деталей
дефектных изделий в выборке с числом деталей 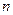 описывается следующим выражением
описывается следующим выражением
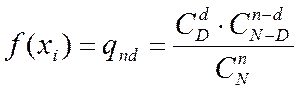 , (1.5)
, (1.5)
где 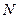 - объем партии изделий;
- объем партии изделий; 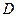 - число дефектных изделий в партии;
- число дефектных изделий в партии; 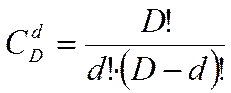 - число сочетаний из
- число сочетаний из 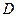 по
по 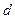 ;
; 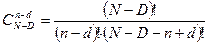 - число сочетаний из
- число сочетаний из 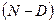 по
по 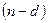 ;
; 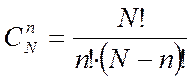 - число сочетаний из
- число сочетаний из 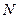 по
по 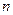 .
.
Величины 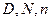 - постоянные, а
- постоянные, а 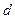 является случайной переменной.
является случайной переменной.
2.При 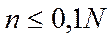 гипергеометрический закон стремится к биномиальному закону, в соответствии с которым вероятность появления дефектных изделий (их количество - d) в выборке объемом
гипергеометрический закон стремится к биномиальному закону, в соответствии с которым вероятность появления дефектных изделий (их количество - d) в выборке объемом 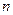 составляет
составляет
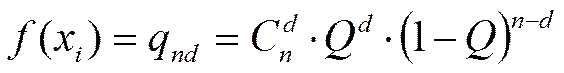 , (1.6)
, (1.6)
где 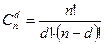 - число сочетаний из
- число сочетаний из 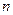 по
по 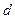 ;
;
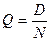 - характеристика контролируемой партии.
- характеристика контролируемой партии.
3.При 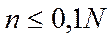 и
и 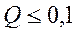 биномиальный закон распределения совпадает с законом Пуассона. При этом вероятность появления дефектных изделий (их количество -
биномиальный закон распределения совпадает с законом Пуассона. При этом вероятность появления дефектных изделий (их количество - 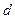 ) в выборке объемом
) в выборке объемом 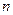 равно
равно 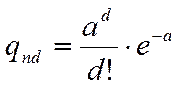 , (1.7)
, (1.7)
где 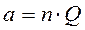 - положительная величина, называемая параметром Пуассона.
- положительная величина, называемая параметром Пуассона.
1. Биномиальное распределение. Дискретная случайная величина X имеет биномиальный закон распределения с параметрами n и p, если она принимает значения 0, 1, 2, …, m, …, n с вероятностями
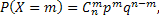
где 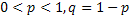 .
.
Биномиальный закон распределения представляет собой закон распределения числа X = m наступлений событий A в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p.
Математическое ожидание: 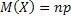 .
.
Дисперсия: 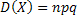 .
.
Биномиальный закон распределения широко используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, при моделировании цен активов, в теории стрельбы и т.д.
2. Распределение Пуассона. Дискретная случайная величина X имеет закон распределения Пуассона с параметром l > 0, если она принимает значения 0, 1, 2, …, m, … (бесконечное, но счетное множество значений) с вероятностями
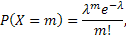
Математическое ожидание: 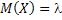 .
.
Дисперсия: 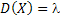 .
.
При достаточно больших n ( 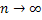 ) и малых значениях р (
) и малых значениях р ( 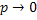 ) при условии, что произведение
) при условии, что произведение 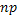 – постоянная величина (
– постоянная величина ( 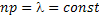 ), закон распределения Пуассона является предельным случаем биномиального закона (закон массовых и редких событий). Кроме этого, по закону Пуассона распределены число сбоев на автоматической линии, число отказов сложной системы в «нормальном режиме», число «требований на обслуживание», поступивших в единицу времени в системах массового обслуживания и др.
), закон распределения Пуассона является предельным случаем биномиального закона (закон массовых и редких событий). Кроме этого, по закону Пуассона распределены число сбоев на автоматической линии, число отказов сложной системы в «нормальном режиме», число «требований на обслуживание», поступивших в единицу времени в системах массового обслуживания и др.
4. Закон распределения Бернулли. Случайная величина 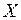 , распределенная по закону Бернулли (индикаторная случайная величина), принимает значения: 1 – «успех» или 0 – «неудача» с вероятностями
, распределенная по закону Бернулли (индикаторная случайная величина), принимает значения: 1 – «успех» или 0 – «неудача» с вероятностями 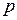 и
и 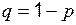 соответственно
соответственно
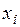 | ||
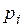 | 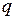 | 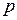 |
Математическое ожидание случайной величины 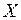 :
: 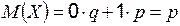 .
.
Дисперсия: 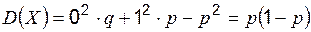 .
.
