Отсутствие универсального ряда для построения признака сходимости
Итак, мы имеем в данный момент три признака сходимости числовых рядов. Два из них (Коши и Даламбера) основаны на сравнении исследуемого ряда с геометрической прогрессией, последний - на сравнении исследуемого ряда с гармоническим рядом. Однако, все эти признаки не являются универсальными и всегда можно привести пример ряда, вопрос о сходимости или расходимости которого не может быть решен с помощью данного признака.
В чем здесь дело? Ряды выбраны неудачно, или найти универсальный ряд для построения признака сходимости принципиально невозможно? Оказывается, верно последнее.
Теорема 1. Для каждого сходящегося ряда можно построить ряд, который
а) также сходится, но
б) вопрос об его сходимости не может быть решен на основании сравнения с исходным рядом.
Доказательство.
Пусть дан сходящийся ряд 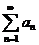 с положительными членами. Пусть
с положительными членами. Пусть 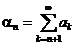 есть его остаток после п-го слагаемого.
есть его остаток после п-го слагаемого.
Построим ряд 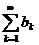 со слагаемыми
со слагаемыми 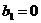 ,
, 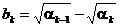 ,
, 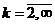 . Что можно сказать об этом ряде?
. Что можно сказать об этом ряде?
а) Имеем
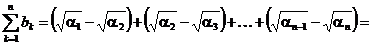
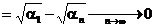 ,
,
так что ряд 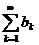 сходится. Но
сходится. Но
б) 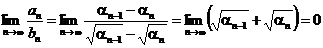
и поэтому теорема 4 не работает и вопрос о сходимости построенного ряда не может быть решен на основании его сравнения с исходным рядом. <
Теорема 2. Для каждого расходящегося ряда можно построить ряд, который
а) также расходится, но
б) вопрос об его расходимости не может быть решен на основании сравнения с исходным рядом.
Доказательство.
Пусть дан расходящийся ряд 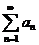 с положительными членами. Обозначим через
с положительными членами. Обозначим через 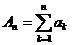 его частную сумму. Расходимость ряда
его частную сумму. Расходимость ряда 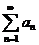 означает, что
означает, что 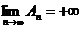 (обозначение:
(обозначение: 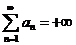 ).
).
Построим ряд 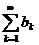 со слагаемыми
со слагаемыми 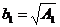 ,
, 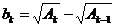 ,
, 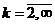 . Что можно сказать об этом ряде?
. Что можно сказать об этом ряде?
а) Имеем
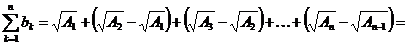
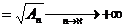 ,
,
то есть 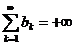 , так что ряд
, так что ряд 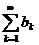 расходится. Но
расходится. Но
б) 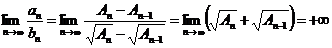
и поэтому теорема 4 не работает и вопрос о расходимости построенного ряда не может быть решен на основании его сравнения с исходным рядом. <
Вывод:не существует универсального ряда, из сравнения с которым можно было бы решить вопрос о сходимости или расходимость всех остальных рядов.
Интегральный признак Коши
Отсутствие универсального ряда для построения признака сходимости не означает, конечно, что не может быть других принципов для построения признаков сходимости числовых рядов. ниже будет разобран достаточно оригинальный признак сходимости, называемый интегральным признаком Коши.
Пусть функция 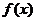
1. определена на промежутке 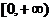 ;
;
2. монотонно убывает и 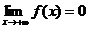 .
.
Рассмотрим ряд вида 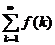 , то есть слагаемые этого ряда имеют вид
, то есть слагаемые этого ряда имеют вид 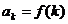 .
.
Теорема. При указанных выше ограничениях ряд 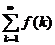 сходится одновременно с несобственным интегралом
сходится одновременно с несобственным интегралом 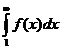 .
.
Доказательство.
1. Основное неравенство.
Обозначим 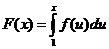 . Так как
. Так как 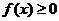 , то
, то 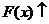 . далее имеем
. далее имеем
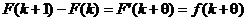 .
.
В силу монотонного убывания 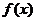
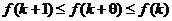 ,
,
и поэтому в данном случае
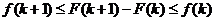 .
.
Это неравенство мы условно будем называть основным неравенством.
2. Пусть интеграл 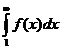 сходится. Это значит, что
сходится. Это значит, что 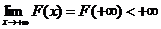 . Но тогда имеем
. Но тогда имеем
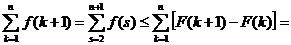
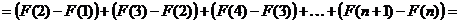
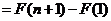 .
.
 | Переходя к пределу 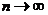 , получаем, что , получаем, что 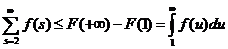 , откуда и следует, что ряд , откуда и следует, что ряд 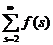 сходится. Возникающая ситуация видна на прилагаемом рисунке: сумма площадей прямоугольников, каждый из которых равен одному слагаемому ряда, меньше площади, ограниченной функцией сходится. Возникающая ситуация видна на прилагаемом рисунке: сумма площадей прямоугольников, каждый из которых равен одному слагаемому ряда, меньше площади, ограниченной функцией 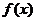 и осью абсцисс. и осью абсцисс. |
3. Пусть ряд 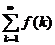 сходится.
сходится.
Тогда имеем
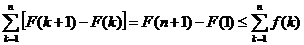 ,
,
то есть 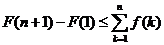 .
.
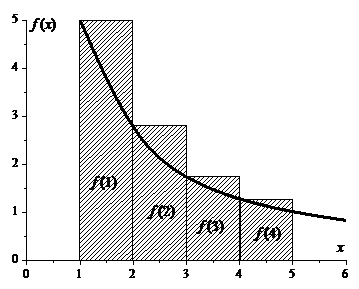 | Переходя к пределу 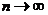 , получаем, что , получаем, что 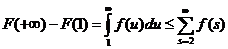 , откуда и следует, что интеграл , откуда и следует, что интеграл 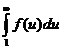 сходится. Возникающая ситуация видна на прилагаемом рисунке: площадь, ограниченная функцией сходится. Возникающая ситуация видна на прилагаемом рисунке: площадь, ограниченная функцией 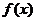 и осью абсцисс, меньше суммы площадей прямоугольников, каждый из которых равен одному слагаемому ряда. < и осью абсцисс, меньше суммы площадей прямоугольников, каждый из которых равен одному слагаемому ряда. < |
