Критерий равенства двух векторов
ОСНОВНЫЕ ПОНЯТИЯ О ВЕКТОРАХ
Определение. Вектором называется направленный отрезок, т.е. отрезок, у которого различают начало и конец.
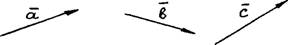 |
Обычно вектор изображают стрелкой и обозначают
 . При рассмотрении нескольких векторов используют также обозначения
. При рассмотрении нескольких векторов используют также обозначения 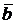 ,
, 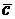 и другие.
и другие. Определение. Длиной (модулем) вектора называется длина отрезка, соединяющего начало и конец вектора.
Длину вектора  обозначают
обозначают 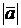 .
.
Определение. Нулевым вектором (нуль-вектором) называется вектор, длина которого равна нулю.
Нуль-вектор будем обозначать 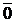 . Нуль-вектор не имеет определенного направления.
. Нуль-вектор не имеет определенного направления.
Определение. Ортом называется вектор, длина которого равна единице.
Орт будем обозначать 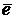 . По определению
. По определению 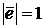 .
.
Определение. Ортом ненулевого вектора называется орт, направление которого совпадает с направлением данного вектора.
Орт вектора  обозначим
обозначим 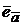 .
.
Определение. Вектор называется свободным, если он задается только направлением и длиной.
Определение. Вектор называется скользящим, если он задается не только направлением и длиной, но, кроме того, фиксируется прямая, на которой он расположен.
Определение. Вектор называется закрепленным, если он задается направлением, длиной и фиксированным началом.
В последующем будем рассматривать преимущественно свободные векторы, однако будут использоваться также и закрепленные векторы. Закрепленный вектор будем обозначать, как правило, двумя буквами, а именно 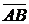 ; здесь
; здесь 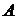 - начало вектора,
- начало вектора, 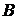 - конец вектора.
- конец вектора.
При рассмотрении нескольких векторов используются также обозначения 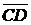 ,
, 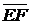 и другие.
и другие.
Длину вектора 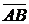 обозначают
обозначают  .
.
Определение. Углом между векторами  и
и 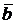 называется угол, на который надо повернуть первый вектор
называется угол, на который надо повернуть первый вектор  , чтобы его направление совпало с направлением второго вектора
, чтобы его направление совпало с направлением второго вектора 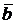 .
.
Угол между векторами  и
и 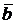 обозначают (
обозначают ( 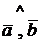 ).
).
Определение. Угол между векторами  и
и 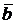 называют положительным, если поворот от вектора
называют положительным, если поворот от вектора  к вектору
к вектору 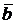 производится против часовой стрелки.
производится против часовой стрелки.

Определение. Угол между векторами  и
и 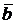 называют отрицательным, если поворот от вектора
называют отрицательным, если поворот от вектора  к вектору
к вектору 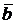 производится по часовой стрелке.
производится по часовой стрелке.
|
 и
и 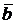 с очевидностью следует, что угол между этими векторами определяется с точностью до слагаемого
с очевидностью следует, что угол между этими векторами определяется с точностью до слагаемого 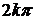 , где
, где 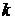 - любое целое число. Действительно, повернув вектор
- любое целое число. Действительно, повернув вектор  на угол
на угол 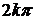 , придем к прежнему положению вектора
, придем к прежнему положению вектора  . Впредь будем полагать, что поворот от вектора
. Впредь будем полагать, что поворот от вектора  к вектору
к вектору 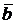 производится до первого совмещения направления первого вектора с направлением второго, т.е. будем считать
производится до первого совмещения направления первого вектора с направлением второго, т.е. будем считать 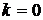 . Условимся, кроме того, поворот от первого вектора ко второму производить, как правило, против часовой стрелки, т.е. будем, как правило, полагать
. Условимся, кроме того, поворот от первого вектора ко второму производить, как правило, против часовой стрелки, т.е. будем, как правило, полагать 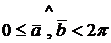 .
.Определение. Два вектора называются коллинеарными, если они расположены на одной или параллельных прямых.
Из этого определения следует, что угол между коллинеарными векторами либо равен 0 (в этом случае векторы называют одинаково направленными), либо равен 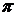 (в этом случае векторы называют противоположно направленными). Для указания того, что
(в этом случае векторы называют противоположно направленными). Для указания того, что  и
и 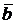 одинаково направленные векторы, используют обозначение
одинаково направленные векторы, используют обозначение  . Если
. Если  и
и 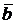 противоположно направленные векторы, то в этом случае пишут
противоположно направленные векторы, то в этом случае пишут 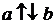 .
.
Определение. Два вектора называются равными, если они имеют одну и ту же длину и одинаково направлены.

Определение. Параллельным переносом вектора называется такой его перенос, при котором сохраняется направление вектора и его длина.
Следовательно, вектор, полученный из данного параллельным переносом, равен данному. Очевидно также, что равные векторы посредством параллельного переноса можно совместить. За счет параллельного переноса можно совместить начала всех рассматриваемых векторов или совместить начало одного из векторов с концом другого.
Определение. Два вектора называются противоположными, если они имеют одну и ту же длину и противоположно направлены.
Определение. Осью называется прямая с выбранным на ней направлением.
Ось будем обозначать буквой 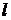 .
.
|

Определение. Ортом оси называется орт, направление которого совпадает с направлением этой оси.
Орт оси 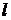 обозначим
обозначим 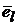 или короче
или короче 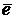 .
.
В дальнейшем направление оси 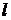 будем задавать её ортом
будем задавать её ортом 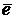 , а угол между осью
, а угол между осью 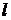 и вектором
и вектором  , будем обозначать
, будем обозначать 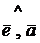 .
.
Определение. Проекцией точки на ось называется точка, являющаяся основанием перпендикуляра, опущенного из этой точки на данную ось.
Определение. Составляющей вектора  по оси
по оси 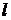 называется вектор, началом которого является проекция начала вектора
называется вектор, началом которого является проекция начала вектора  на ось
на ось 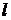 , а концом - проекция конца вектора
, а концом - проекция конца вектора  на ту же ось
на ту же ось 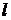 .
.
Составляющую вектора  по оси
по оси 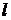 обозначим
обозначим 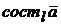 .
.
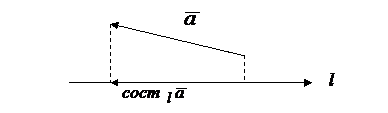
| |
 на ось
на ось 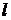 называется число, модуль которого равен длине составляющей вектора
называется число, модуль которого равен длине составляющей вектора  по оси
по оси  , причем это число положительно, если составляющая вектора
, причем это число положительно, если составляющая вектора  по оси
по оси 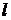 и ось
и ось  одинаково направлены, и отрицательно, если составляющая вектора
одинаково направлены, и отрицательно, если составляющая вектора  по оси
по оси 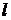 и ось
и ось  противоположно направлены.
противоположно направлены. Проекцию вектора  на ось
на ось 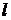 обозначают
обозначают 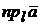 или
или 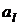 .
.
Доказательство.
Необходимость. Пусть 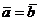 , тогда векторы
, тогда векторы  и
и  можно совместить, и потому, очевидно,
можно совместить, и потому, очевидно, 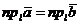 , где
, где  - любая ось.
- любая ось.
Нетрудно показать справедливость утверждения и без совмещения векторов.
Достаточность. Пусть 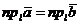 , где
, где  - любая ось. Докажем, что
- любая ось. Докажем, что 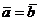 .
.
Предположим противное: 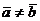 . Убедимся в том, что при этом предположении найдется хотя бы одна такая ось, что проекции векторов
. Убедимся в том, что при этом предположении найдется хотя бы одна такая ось, что проекции векторов  и
и  на эту ось не будут равны между собой.
на эту ось не будут равны между собой.
Рассмотрим два возможных случая:
1). Векторы  и
и  коллинеарны.
коллинеарны.
Совместим начала этих векторов и проведем ось  так, чтобы рассматриваемые векторы оказались расположенными на этой оси.
так, чтобы рассматриваемые векторы оказались расположенными на этой оси.
При этом:
а) Если векторы  и
и  одинаково направлены, то в силу того, что их длины различны (иначе оказалось бы, что
одинаково направлены, то в силу того, что их длины различны (иначе оказалось бы, что 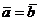 ), концы векторов
), концы векторов  и
и  не совпадут. Очевидно, что тогда составляющие векторов
не совпадут. Очевидно, что тогда составляющие векторов  и
и  по оси
по оси  будут иметь различные длины и, следовательно,
будут иметь различные длины и, следовательно, 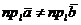 , что противоречит условию утверждения.
, что противоречит условию утверждения.
б). Если векторы  и
и  противоположно направлены, то, очевидно, и составляющие этих векторов по оси
противоположно направлены, то, очевидно, и составляющие этих векторов по оси  имеют противоположные направления. В этом случае проекции векторов
имеют противоположные направления. В этом случае проекции векторов  и
и  на ось являются числами разных знаков, и потому
на ось являются числами разных знаков, и потому 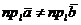 , что противоречит условию утверждения.
, что противоречит условию утверждения.
2). Векторы  и
и  неколлинеарны.
неколлинеарны.
Совместим начала векторов  и
и  и проведем ось
и проведем ось  через общее начало
через общее начало  и
и  перпендикулярно биссектрисе угла
перпендикулярно биссектрисе угла 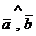 .
.
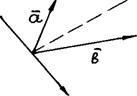
Составляющие векторов  и
и  по оси
по оси  будут иметь противоположные направления. В этом случае проекции векторов
будут иметь противоположные направления. В этом случае проекции векторов  и
и  на ось
на ось  являются числами разных знаков, и потому
являются числами разных знаков, и потому 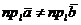 , что противоречит условию утверждения.
, что противоречит условию утверждения.
Итак, предположение, что 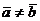 , противоречит условию утверждения, следовательно,
, противоречит условию утверждения, следовательно, 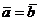 .
.
Координаты точек на прямой
Определение. Числовой осью называется ось с выбранным на ней началом отсчета и масштабом.
|
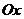 . Точка
. Точка 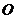 − начало отсчета. Орт числовой оси
− начало отсчета. Орт числовой оси 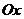 обозначим через
обозначим через 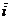 .
.
|
|
|

Пусть 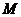 − произвольная точка на числовой оси
− произвольная точка на числовой оси 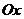 .
.
Определение. Радиусом-вектором точки 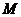 на числовой оси называется вектор, началом которого является точка
на числовой оси называется вектор, началом которого является точка 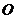 , а концом - точка
, а концом - точка 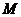 .
.
Из определения очевидно, что радиус-вектор точки 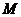 - закрепленный вектор.
- закрепленный вектор.
Определение. Координатой точки 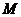 на числовой оси
на числовой оси 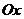 называется проекция радиуса-вектора точки
называется проекция радиуса-вектора точки 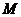 на рассматриваемую ось.
на рассматриваемую ось.
Координату точки 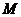 на числовой оси
на числовой оси 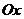 обозначим буквой
обозначим буквой 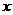 . При этом обычно употребляется следующая запись:
. При этом обычно употребляется следующая запись: 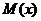 .
.
Итак, по определению,
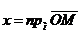 .
.
Можно доказать, что между множеством точек на числовой оси и множеством вещественных чисел существует взаимнооднозначное соответствие, т.е. каждой точке на числовой оси соответствует определенное вещественное число, являющееся координатой этой точки на рассматриваемой оси, и каждому вещественному числу соответствует на числовой оси определенная точка, для которой указанное число является координатой на этой оси.
СЛОЖЕНИЕ ВЕКТОРОВ
Пусть даны свободные векторы  и
и  . Совместим начало второго вектора
. Совместим начало второго вектора  с концом первого вектора
с концом первого вектора  .
.
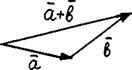 Определение. Суммой двух векторов
Определение. Суммой двух векторов  и
и  называется вектор, началом которого является начало первого из складываемых векторов
называется вектор, началом которого является начало первого из складываемых векторов  , а концом - конец второго вектора
, а концом - конец второго вектора  , при этом разумеется, что начало второго из складываемых векторов совмещено с концом первого.
, при этом разумеется, что начало второго из складываемых векторов совмещено с концом первого.
Сумма векторов  и
и  обозначается
обозначается 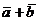 .
.
Из определения следует, что
1) сумма двух противоположных векторов есть нуль-вектор,
2) сумма вектора  и нуль-вектора равна вектору
и нуль-вектора равна вектору  .
.
Теорема(о проекции суммы двух векторов на ось). Проекция суммы двух векторов на ось равна сумме проекций складываемых векторов на ту же ось, т.е.
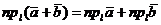
где  - любая ось.
- любая ось.
Доказательство. Наряду с осью  рассмотрим числовую ось
рассмотрим числовую ось  , совмещенную с осью
, совмещенную с осью  и одинаково с ней направленную. Тогда, очевидно,
и одинаково с ней направленную. Тогда, очевидно,
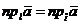 ,
, 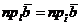 ,
, 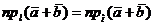
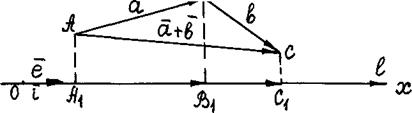
Согласно чертежу, 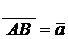 ,
, 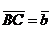 ,
, 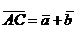 ;
;
 ,
, 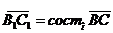 ,
, 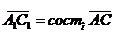
По теореме о проекции вектора на числовую ось
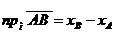 и
и 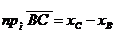
где 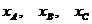 - соответственно координаты точек
- соответственно координаты точек 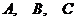 на числовой оси
на числовой оси 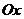 . Складывая почленно эти равенства, получим
. Складывая почленно эти равенства, получим
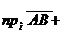
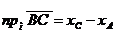
С другой стороны, на основании теоремы о проекции вектора на числовую ось
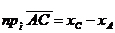
Из двух последних равенств вытекает 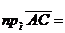
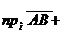
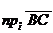 или, что, согласно чертежу, то же самое,
или, что, согласно чертежу, то же самое, 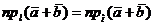 , что и требовалось доказать.
, что и требовалось доказать.
УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
Определение. Произведением вектора  на скаляр
на скаляр 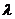 называется вектор, модуль которого равен произведению модулей сомножителей, а направление совпадает с направлением вектора
называется вектор, модуль которого равен произведению модулей сомножителей, а направление совпадает с направлением вектора  , если число
, если число 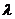 положительно, и противоположно направлению вектора
положительно, и противоположно направлению вектора  , если число
, если число 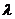 отрицательно.
отрицательно.
Произведение вектора  на скаляр
на скаляр 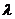 обозначается
обозначается  или
или  . По определению:
. По определению:
1.  ;
;
2.  , если
, если  ,
,  , если
, если  ;
;
3. если  , то
, то  ;
;
4. если  , то
, то  .
.
Согласно определению, произведение вектора  на скаляр
на скаляр 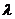 есть вектор, коллинеарный вектору
есть вектор, коллинеарный вектору  .
.
Теорема (о проекции на ось произведения вектора на скаляр). Проекция на ось произведения вектора на скаляр равна произведению этого скаляра на проекцию рассматриваемого вектора на ту же ось, т.е.
 ,
,
где  - любая ось.
- любая ось.
Доказательство. По теореме о проекции вектора на ось
 ,
,
где 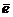 - орт оси
- орт оси  . Если в правой части этого равенства воспользоваться определением понятия модуля произведения вектора на скаляр, то получим
. Если в правой части этого равенства воспользоваться определением понятия модуля произведения вектора на скаляр, то получим
 (*)
(*)
При этом возможны следующие случаи:
1.  .
.
В этом случае по определению модуля числа  . Кроме того, при
. Кроме того, при 
 , и поэтому
, и поэтому  . Следовательно, в силу равенства (*) имеем
. Следовательно, в силу равенства (*) имеем
 .
.
Если теперь в правой части последнего равенства воспользоваться свойством сочетательности умножения чисел и применить теорему о проекции вектора на ось, то получим
 .
.
2. 
В этом случае по определению модуля числа  . Кроме того, при
. Кроме того, при 
 , т.е.
, т.е.  и потому
и потому  .
.


Исходя из равенства (*), приходим к выводу, что в рассматриваемом случае
 ,
,
и потому, как и при  , имеем
, имеем
 .
.
В справедливости утверждения при  предлагаем убедиться самостоятельно.
предлагаем убедиться самостоятельно.
Следствия
1). Длина вектора равна арифметическому значению корня квадратного из суммы квадратов проекций этого вектора на координатные оси:
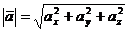 .
.
Доказательство. Действительно, 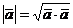 и так как
и так как 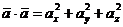 , то
, то 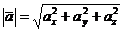 .
.
2). Расстояние между точками 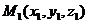 и
и 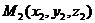 равно арифметическому значению корня квадратного из суммы квадратов разностей одноименных декартовых координат этих точек, то есть
равно арифметическому значению корня квадратного из суммы квадратов разностей одноименных декартовых координат этих точек, то есть
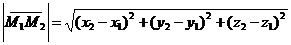 .
.
Доказательство. Действительно, 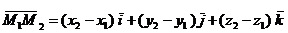 и потому
и потому 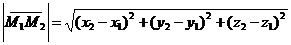 .
.
3). Сумма квадратов направляющих косинусов любого вектора равна единице, то есть
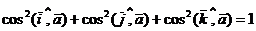 .
.
Доказательство. Как было показано ранее, для орта вектора  справедливо следующее равенство:
справедливо следующее равенство: 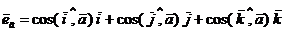 . Кроме того,
. Кроме того, 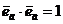 . Следовательно,
. Следовательно, 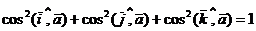 .
.
ДВУХ ВЕКТОРОВ
1. Векторное произведение двух векторов обладает свойством антипереместительности:
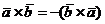 .
.
Доказательство. Для того, чтобы доказать, что векторы 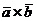 и
и 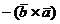 равны, докажем, что равны их проекции на любую ось. Пусть
равны, докажем, что равны их проекции на любую ось. Пусть  - произвольная ось. По свойству 3 скалярного произведения двух векторов
- произвольная ось. По свойству 3 скалярного произведения двух векторов
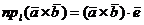 ,
,
где 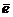 - орт оси
- орт оси  . С учетом свойства 3 смешанного произведения трёх векторов это равенство принимает вид
. С учетом свойства 3 смешанного произведения трёх векторов это равенство принимает вид
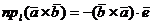 .
.
Если же теперь в правой части применить свойства 3 и 4 скалярного произведения двух векторов, то получим 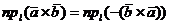 , где
, где  - любая ось.
- любая ось.
Следовательно, согласно критерию равенства двух векторов 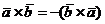 .
.
2. Скалярный множитель можно вынести за знак векторного произведения двух векторов:
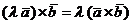 и
и 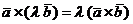
Доказательство. Убедимся в справедливости первого равенства. Для этого достаточно доказать, что 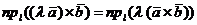 где
где  - любая ось. По свойству 3 скалярного произведения двух векторов
- любая ось. По свойству 3 скалярного произведения двух векторов
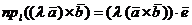 ,
,
где 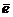 - орт оси
- орт оси  . С учетом свойства цикличности смешанного произведения трёх векторов это равенство принимает вид
. С учетом свойства цикличности смешанного произведения трёх векторов это равенство принимает вид
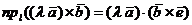 ,
,
или, в силу свойства 4 скалярного произведения двух векторов,
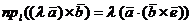 .
.
Если же в правой части этого равенства вновь воспользоваться свойством цикличности смешанного произведения трёх векторов и свойством 3 скалярного произведения двух векторов, то имеем
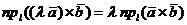 .
.
Учитывая теорему о проекции на ось произведения вектора на скаляр, получим
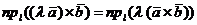
где  - любая ось, и потому, согласно критерию равенства двух векторов,
- любая ось, и потому, согласно критерию равенства двух векторов,
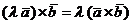 .
.
Аналогично можно доказать справедливость второго равенства.
3. Векторное произведение двух векторов обладает свойством распределительности, то есть
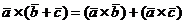 .
.
Доказательство. Докажем, что 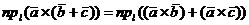 где
где  - произвольная ось. По свойству 3 скалярного произведения двух векторов
- произвольная ось. По свойству 3 скалярного произведения двух векторов
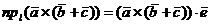 ,
,
где 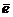 - орт оси
- орт оси  . С учетом свойства цикличности смешанного произведения трех векторов это равенство принимает вид
. С учетом свойства цикличности смешанного произведения трех векторов это равенство принимает вид
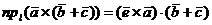 .
.
В силу свойства распределительности скалярного произведения двух векторов имеем
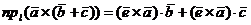 .
.
В каждом слагаемом правой части последнего равенства вновь применим свойство цикличности смешанного произведения трех векторов. Тогда получим
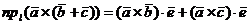 ,
,
или, с учетом свойства распределительности скалярного произведения,
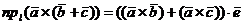 .
.
Если же ещё раз воспользоваться свойством 3 скалярного произведения двух векторов, то придем к выводу, что
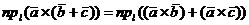
где  - любая ось, и потому, согласно критерию равенства двух векторов,
- любая ось, и потому, согласно критерию равенства двух векторов,
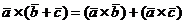 .
.
4. 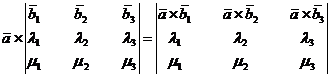 .
.
Доказательство. Воспользуемся равенством:
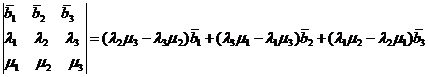 .
.
Тогда, в силу свойств 2 и 3 векторного произведения двух векторов, имеем
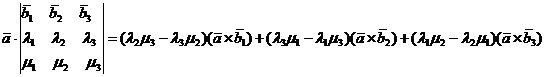
то есть
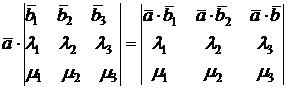 .
.
5. Векторное произведение вектора самого на себя есть нуль-вектор:
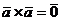 .
.
Доказательство. Справедливость этого утверждения с очевидностью следует из определения векторного произведения двух векторов.
6. Имеет место следующая таблица векторных произведений координатных ортов:
| Второй множитель | ||||
| Первый множитель | 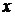 | 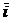 | 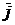 | 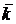 |
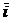 | 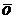 | 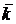 | 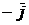 | |
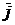 | 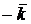 | 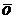 | 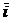 | |
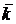 | 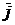 | 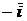 | 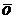 |
Справедливость этой таблицы следует из определения векторного произведения двух векторов.
7. Векторное произведение векторов  и
и  может быть представлено через проекции этих векторов на координатные оси по следующей формуле:
может быть представлено через проекции этих векторов на координатные оси по следующей формуле:
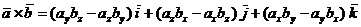
или, что то же самое,
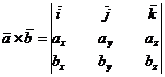 .
.
Доказательство. Разложим каждый из векторов  и
и  по координатным ортам:
по координатным ортам: 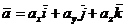 и
и 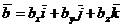 .
.
Воспользовавшись свойствами 2 и 3 векторного произведения двух векторов, имеем 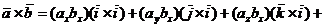
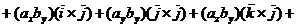
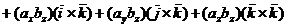 ,
,
или, с учетом таблицы векторных произведений координатных ортов,
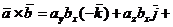
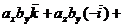
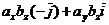 .
.
В силу свойств сочетательности и распределительности произведения вектора на скаляр, получим 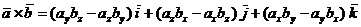 , или, что то же самое,
, или, что то же самое, 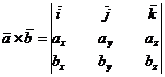 .
.
УГОЛ МЕЖДУ ВЕКТОРАМИ
Для отыскания угла между двумя векторами воспользуемся определением скалярного произведения двух векторов: 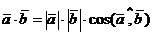 .
.
Предполагая, что  и
и  - не нуль-векторы, получим
- не нуль-векторы, получим
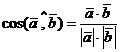 . (1)
. (1)
Если заданы проекции рассматриваемых векторов на координатные оси то равенство (1) можно представить в виде
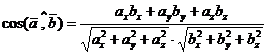 .
.
Учитывая, что для ортов ненулевых векторов  и
и  справедливы равенства
справедливы равенства
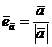 и
и 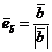 ,
,
получаем, в силу (1),
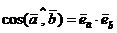 .
.
КРИТЕРИИ КОМПЛАНАРНОСТИ ТРЁХ ВЕКТОРОВ
Первый критерий компланарности трёх векторов
Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы смешанное произведение этих векторов было равно нулю:
Векторы  , ,  , ,  компланарны компланарны |  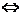 | 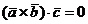 |
Доказательство. Необходимость. Пусть векторы  ,
,  ,
, 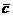 компланарны, следовательно, по определению, существует плоскость, которой эти векторы параллельны. Вектор
компланарны, следовательно, по определению, существует плоскость, которой эти векторы параллельны. Вектор 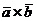 , по определению, перпендикулярен каждому из векторов
, по определению, перпендикулярен каждому из векторов  и
и  . Значит, вектор
. Значит, вектор 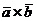 перпендикулярен вектору
перпендикулярен вектору 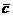 , и потому, согласно первому критерию перпендикулярности векторов,
, и потому, согласно первому критерию перпендикулярности векторов, 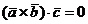 .
.
Достаточность. Пусть 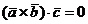 , тогда
, тогда 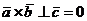 . Если, кроме того, учесть, что вектор
. Если, кроме того, учесть, что вектор 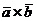 перпендикулярен каждому из векторов
перпендикулярен каждому из векторов  и
и  , то придем к выводу, что векторы
, то придем к выводу, что векторы  ,
,  ,
, 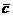 компланарны.
компланарны.
Второй критерий компланарности трёх векторов
Для того, чтобы векторы  ,
,  ,
, 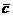 были компланарны, необходимо и достаточно, чтобы выполнялось равенство
были компланарны, необходимо и достаточно, чтобы выполнялось равенство
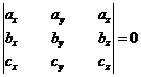 .
.
Доказательство. Справедливость этого утверждения вытекает из предыдущего критерия с учетом теоремы о представлении смешанное произведения трёх векторов через их проекции на координатные оси.
Третий критерий компланарности трёх векторов
Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы они были линейно зависимы:
Векторы  , ,  , , 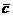 компланарны компланарны |   | Векторы  , ,  , , 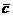 линейно зависимы линейно зависимы |
Доказательство. Необходимость. Для того, чтобы показать, что векторы  ,
,  ,
, 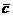 линейно зависимы докажем, что если векторы
линейно зависимы докажем, что если векторы  и
и