Общие правила комбинаторики. Прямое произведение множеств и правило произведения.
Комбинаторика−это наука о конечных множествах. Мы будем изучать лишь ту ее часть, в которой нужно найти число элементов множества, которое получается из других конечных множеств с помощью специальных операций.
Определение. Пусть 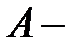 конечное множество, Тогда
конечное множество, Тогда 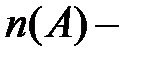 число элементов множества
число элементов множества 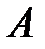 , при этом говорят, что объект из множества
, при этом говорят, что объект из множества 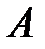 может быть выбран
может быть выбран 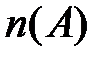 способами.
способами.
Ясно, что 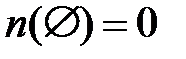 и всегда
и всегда 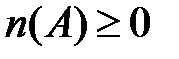 . Изучим некоторые свойства меры
. Изучим некоторые свойства меры 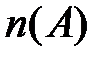 , введенной для любого конечного множества
, введенной для любого конечного множества 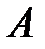 .
.
Свойство 2.1(правило суммы или свойство конечной аддитивности меры 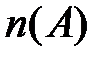 ). Верны утверждения:
). Верны утверждения:
1)если 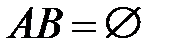 , то
, то 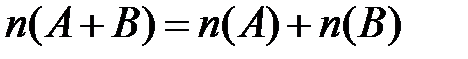 ;
;
2)если 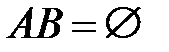 ,
, 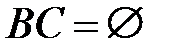 и
и 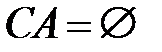 , то
, то 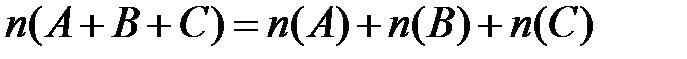 ;
;
3)если 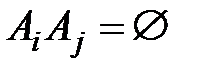 ,
, 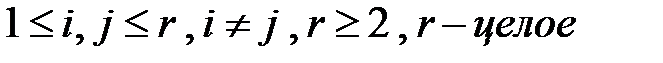 ,
,
то 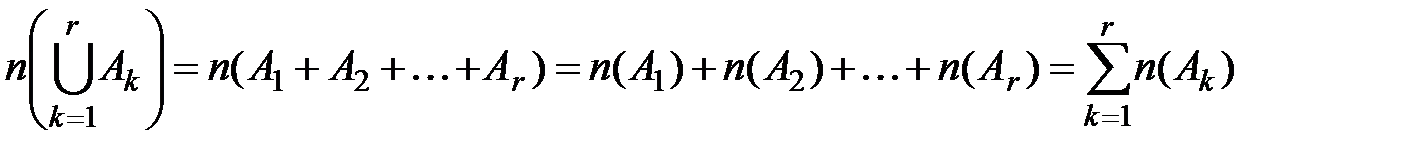 .
.
Свойство 2.2(правило объединения).
Верны утверждения:
1) 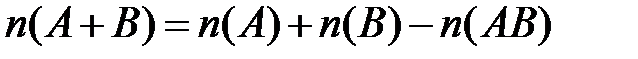 ;
;
2) 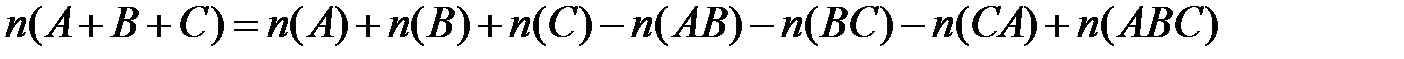 .
.
Свойство 2.3(правило разности).
Верны утверждения:
1) 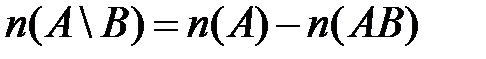 ;
;
2) 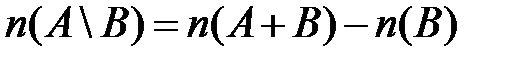 ;
;
3) если 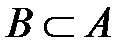 , то
, то 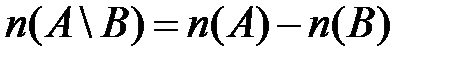 .
.
Свойство 2.4 (свойство монотонности меры 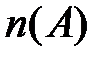 ).
).
если 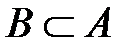 , то
, то 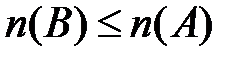 .
.
Свойство 2.5(правило произведения).
Верны утверждения:
1) 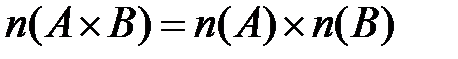 ;
;
2) 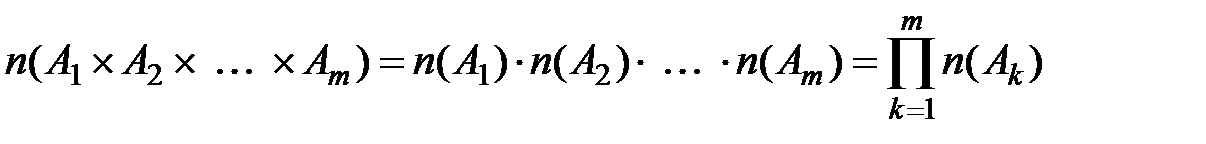 .
.
Пример 2.1(задача о значках). Пусть имеются три набора (множества) объектов:
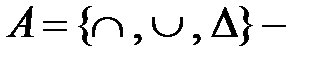 множество математических символов;
множество математических символов;
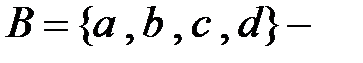 множество букв;
множество букв;
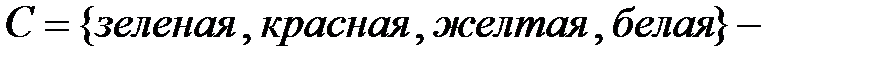 множество красок.
множество красок.
На математический символ наклеивают букву, новую заготовку окрашивают и получают значок. Сколько разных значков можно сделать?
Решение.
Способ 1. На математический символ наклеивают букву и получают новую заготовку. Число новых заготовок равно, очевидно, числу клеток таблицы 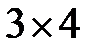 и равно 12. Новую заготовку окрашивают и получают значок. Число значков равно, очевидно, числу клеток таблицы
и равно 12. Новую заготовку окрашивают и получают значок. Число значков равно, очевидно, числу клеток таблицы 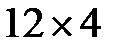 и равно 48.
и равно 48.
Способ 2. Пусть 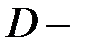 множество значков. Ясно, что
множество значков. Ясно, что 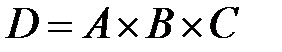 . По правилу произведения
. По правилу произведения 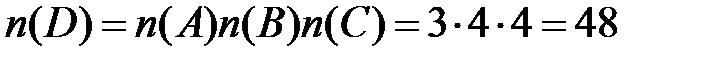 .
.
Способ 3. По правилу произведения число разных значков равно 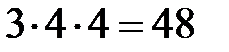 .
.
На практике решение задач похожих на задачу о значках обычно оформляется так, как показано в способе 3.
Размещения без повторений. Размещения с повторениями. Перестановки без повторений. Перестановки с повторениями.
Размещения без повторений.
Предположим, что в урне лежат 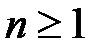 разных объектов, которых будем называть буквами. Из этой урны без возвращения вытаскиваем последовательно
разных объектов, которых будем называть буквами. Из этой урны без возвращения вытаскиваем последовательно 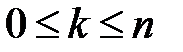 букв. Получается слово длины
букв. Получается слово длины 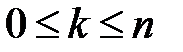 , если буква, появившаяся при вытаскивании с номером
, если буква, появившаяся при вытаскивании с номером 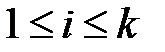 , вставляется в это слово на место с таким же номером
, вставляется в это слово на место с таким же номером 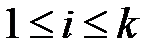 . Полученное слово называется размещением без повторений из
. Полученное слово называется размещением без повторений из 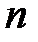 элементов по
элементов по 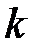 элементов.
элементов.
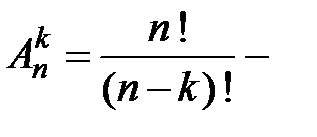 число всех размещений без повторений из
число всех размещений без повторений из 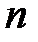 элементов по
элементов по 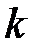 элементов,
элементов,
где 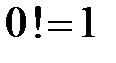 ,
, 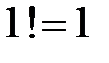 ,
, 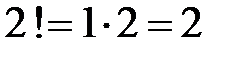 ,
, 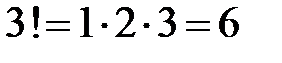 , … ,
, … , 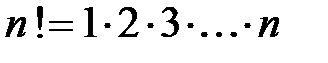 (читается: эн факториал). Если
(читается: эн факториал). Если 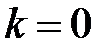 , то получается одно пустое слово и
, то получается одно пустое слово и 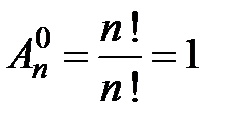 .
.
Пример 3.1. Пусть 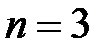 ,
, 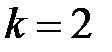 и в урне лежат три буквы
и в урне лежат три буквы 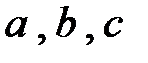 . Найти
. Найти 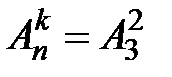 .
.
Решение.
1)Нахождение 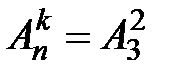 с помощью явного указания всех размещений из
с помощью явного указания всех размещений из 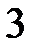 элементов по
элементов по 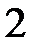 элемента:
элемента: 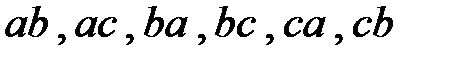 ;
; 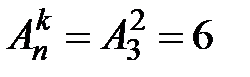 .
.
2) 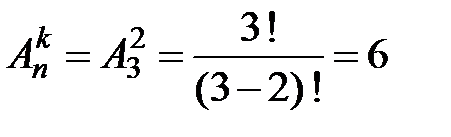 .
.
Размещения с повторениями.
Предположим, что в урне лежат 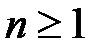 разных объектов, которых будем называть буквами. Из этой урны с возвращением вытаскиваем последовательно
разных объектов, которых будем называть буквами. Из этой урны с возвращением вытаскиваем последовательно  букв. Получается слово длины
букв. Получается слово длины 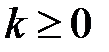 , если буква, появившаяся при вытаскивании с номером
, если буква, появившаяся при вытаскивании с номером 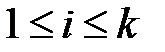 , вставляется в это слово на место с таким же номером
, вставляется в это слово на место с таким же номером 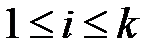 . Полученное слово называется размещением с повторением из
. Полученное слово называется размещением с повторением из 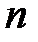 элементов по
элементов по 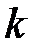 элементов.
элементов.
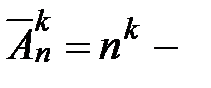 число всех размещений с повторениями из
число всех размещений с повторениями из 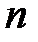 элементов по
элементов по 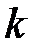 элементов.
элементов.
Если 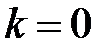 , то получается одно пустое слово и
, то получается одно пустое слово и 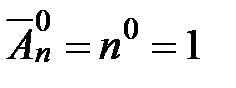 .
.
Пример 3.2. Пусть 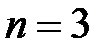 ,
, 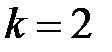 и в урне лежат три буквы
и в урне лежат три буквы 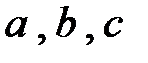 . Найти
. Найти 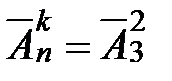 .
.
Решение.
1)Нахождение 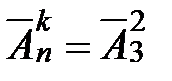 с помощью явного указания всех размещений из
с помощью явного указания всех размещений из 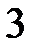 элементов по
элементов по 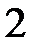 элемента:
элемента: 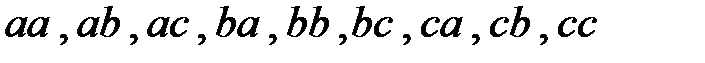 ;
; 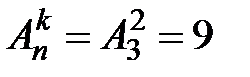 .
.
2) 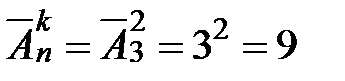 .
.
