Определители 2-го порядка и 3-го порядка, их свойства.
Тема 1. Матрицы и системы
Понятие матрицы
Определение 1. Матрицей размером 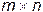 называется прямоугольная таблица чисел или буквенных выражений
называется прямоугольная таблица чисел или буквенных выражений 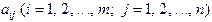 , записанных в виде
, записанных в виде

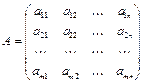 .
.
Здесь, aij (i=1,2,...,m; j=1,2,...n) - элементы матрицы, i- номер строки, j - номер столбца. Матрицы обычно обозначаются большими буквами латинского алфавита A, B, Cи т.д., а также 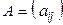 или
или 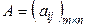 . При m=n матрица называется квадратной матрицей порядка n.
. При m=n матрица называется квадратной матрицей порядка n.
Квадратная матрица, у которой все элементы с неравными индексами i¹j равны нулю, называется диагональной:
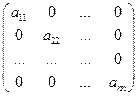
Если все отличные от нуля элементы диагональной матрицы равны единице, то матрица называется единичной. Единичную матрицу принято обозначать буквой E.
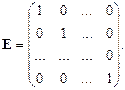
Матрица, все элементы которой равны нулю, называется нулевой и обозначается θ.
Существуют также матрицы, состоящие из одной строки или из одного столбца.
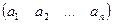 - матрица строка;
- матрица строка; 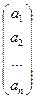 - матрица столбец.
- матрица столбец.
Числовой характеристикой квадратной матрицы является определитель (или детерминант).
Определители 2-го порядка и 3-го порядка, их свойства.
Определители 2-го порядка
Определение 2. Определителем второго порядка матрицы 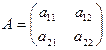 (или просто определителем второго порядка) называется число, обозначаемое символом
(или просто определителем второго порядка) называется число, обозначаемое символом 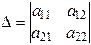 и определяемое равенством
и определяемое равенством 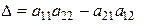 , то есть
, то есть
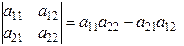 . (3)
. (3)
Другие обозначения: 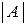 ,
, 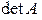 .
.
Таким образом, понятие определителя предполагает одновременно и способ его вычисления. Числа 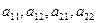 называются элементами определителя. Диагональ, образованная элементами
называются элементами определителя. Диагональ, образованная элементами 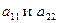 , называется главной, а элементами
, называется главной, а элементами 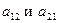 - побочной.
- побочной.
Пример 1. Определитель матрицы 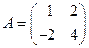 равен
равен
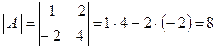 .
.
Определители 3-го порядка
Определение 2. Определителем третьего порядка называется число, обозначаемое символом
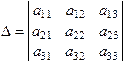 ,
,
и определяемое равенством
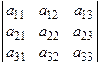 =
= 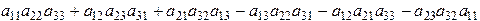 . (4)
. (4)
Числа 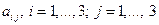 - элементы определителя. Элементы
- элементы определителя. Элементы 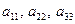 образуют главную диагональ, элементы
образуют главную диагональ, элементы 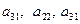 - побочную.
- побочную.
При вычислении определителя чтобы запомнить, какие слагаемые в правой части равенства (4) берутся со знаком «+», а какие со знаком «-», пользуются символическим правилом треугольников (правилом Саррюса):
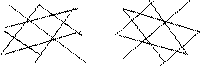
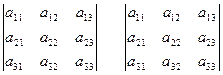
(+) (-)
Со знаком «+» берутся произведения элементов главной диагонали и элементов, находящихся в вершинах треугольников с основаниями, параллельными главной диагонали; сл знаком «-» – произведения элементов побочной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными побочной диагонали.
Вычисление определителя по правилу приписывания столбцов.
1. Приписываем справа от определителя последовательно первый и второй столбцы.
2. Вычисляем произведения трех элементов по диагонали слева - направо, сверху - вниз от а11 до а13 и берем их со знаком «+». Затем вычисляем произведения трех элементов по диагонали слева - направо, снизу вверх от а31 до а13 и берем их со знаком «-».

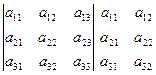
(-) (-) (-) (+) (+) (+)
Пример 2. Вычислить определитель 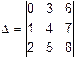 по правилу приписывания столбцов.
по правилу приписывания столбцов. 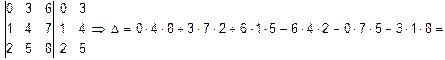
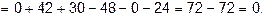
3. Определители n-ого порядка. Миноры и алгебраические дополнения. Вычисление определителей разложением по строке (столбцу).
Рассмотрим понятие определителя n-ного порядка. Определителем n-ного порядка называется число, сопоставляемое матрице n-ного порядка и вычисляемое по определенному закону.
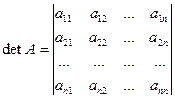 ,
,
здесь 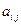 - элементы определителя. Чтобы показать правило, по которому раскрывается определитель n-ного порядка, рассмотрим некоторые понятия.
- элементы определителя. Чтобы показать правило, по которому раскрывается определитель n-ного порядка, рассмотрим некоторые понятия.
Определение 4. Минором 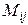 элемента
элемента 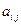 определителя n-го порядка называется определитель (n - 1) порядка, полученный вычеркиванием строки и столбца определителя, на пересечении которых расположен этот элемент.
определителя n-го порядка называется определитель (n - 1) порядка, полученный вычеркиванием строки и столбца определителя, на пересечении которых расположен этот элемент.
Определение 5. Алгебраическим дополнением 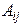 некоторого элемента
некоторого элемента 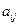 определителя n-го порядка называется минор этого элемента, умноженный на
определителя n-го порядка называется минор этого элемента, умноженный на 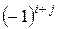 , то есть
, то есть 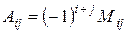 .
.
В определителе третьего порядка 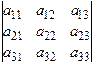 можно рассмотреть, например,
можно рассмотреть, например,
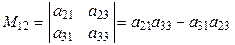 ,
, 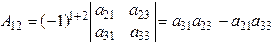 .
.
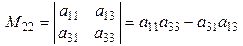 ,
, 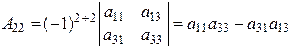 .
.
Определение 6.Определителем n-ного порядка называется число, равное сумме произведений элементов первой строки определителя, умноженных на их алгебраические дополнения.
Это правило вычисления определителя называется разложением по первой строке.
Теорема ( о разложении определителя). Определитель можно вычислить разложением по любой строке или столбцу.
– сумма произведений элементов 1-го столбца на алгебраические дополнения 2-го столбца.
Пример 3. Вычислить определитель четвертого порядка 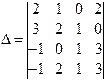 .
.
Решение. Умножаем третью строку на (-1) и прибавляем ее к четвертой, затем раскладываем определитель по четвертой строке:
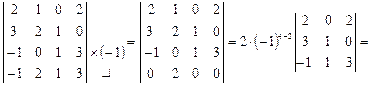
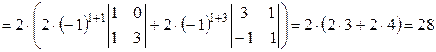 .
.
Определитель третьего порядка разложили по первой строке.
Метод Гаусса.
Метод Гаусса заключается в том, что исходную систему путем исключения неизвестный преобразуют к ступенчатому виду. При этом преобразования выполняются над строками в расширенной матрице, так как преобразования, исключающие неизвестные эквивалентны элементарным преобразованиям строк матрицы.
Метод Гаусса состоит из прямого хода и обратного хода. Прямым ходом метода Гаусса является приведение расширенной матрицы системы (1) к ступенчатому виду путем элементарных преобразований над строками. После чего происходит исследование системы на совместность и определенность. Затем по ступенчатой матрице восстанавливается система уравнений. Решение этой ступенчатой системы уравнений является обратным ходом метода Гаусса, в котором, начиная с последнего уравнения, последовательно вычисляются неизвестные с большим порядковым номером, и их значения подставляются в предыдущее уравнение системы.
Исследование системы в конце прямого хода происходим по теореме Кронекера-Капелли сравнением рангов матрицы системы А и расширенной матрицы А´. При этом возможны следующие случаи.
1) Если 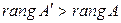 , то система несовместна (по теореме Кронекера-Капелли).
, то система несовместна (по теореме Кронекера-Капелли).
2) Если 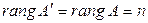 , то система (1) является определенной, и наоборот (без доказательства).
, то система (1) является определенной, и наоборот (без доказательства).
3) Если 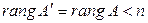 , то система (1) является неопределенной, и наоборот (без доказательства).
, то система (1) является неопределенной, и наоборот (без доказательства).
Неравенство 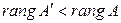 не имеет места, так как матрица А является частью матрицы А´, неравенство
не имеет места, так как матрица А является частью матрицы А´, неравенство 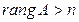 не имеет места, так как число столбцов матрицы А равно п. Кроме того, для системы с квадратной матрицей, то есть если п = т, равенства
не имеет места, так как число столбцов матрицы А равно п. Кроме того, для системы с квадратной матрицей, то есть если п = т, равенства 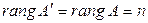 равносильны тому, что
равносильны тому, что 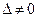 .
.
Если система является неопределенной, то есть выполняется 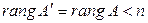 , то некоторые ее неизвестные объявляются свободными, а остальные через них выражаются. Количество свободных неизвестных равно
, то некоторые ее неизвестные объявляются свободными, а остальные через них выражаются. Количество свободных неизвестных равно  . При выполнении обратного хода метода Гаусса, если в очередном уравнении после подстановки найденных ранее переменных, неизвестных осталось более одного, то свободными неизвестными объявляются любые неизвестные, кроме одного.
. При выполнении обратного хода метода Гаусса, если в очередном уравнении после подстановки найденных ранее переменных, неизвестных осталось более одного, то свободными неизвестными объявляются любые неизвестные, кроме одного.
Рассмотрим реализацию метода Гаусса на примерах.
Пример 4. Решить систему уравнений 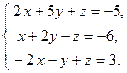
Решение. Решим систему методом Гаусса. Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду элементарными преобразованиями строк (прямой ход).

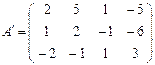 ~
~ 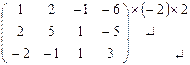 ~
~ 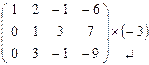 ~
~
~ 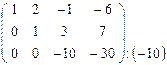 ~
~ 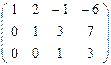 .
.
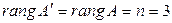 , поэтому система совместна и имеет единственное решение, т.е. является определенной.
, поэтому система совместна и имеет единственное решение, т.е. является определенной.
Составим систему ступенчатого вида и решим ее (обратный ход).
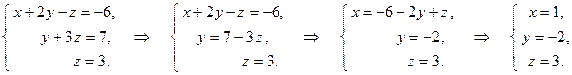
Проверку легко сделать подстановкой.
Ответ: 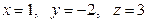 .
.
Тема 2. Векторная алгебра.
Проекция вектора на ось.
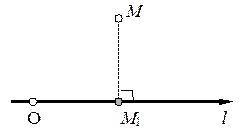 Рис. 1. Рис. 1. |
Под осью понимается прямая линия, на которой задано начало отсчета, масштаб и положительное направление.
Определение 1. Проекцией точки М на ось l называется точка М1, которая является основанием перпендикуляра, проведенного из точки М на эту ось (см. рис.1).
 Рис.2. Рис.2. |
Определение 2.Проекцией вектора 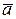 на ось l называется число равное длине отрезка АВ этой оси, заключенного между проекциями начала и конца вектора
на ось l называется число равное длине отрезка АВ этой оси, заключенного между проекциями начала и конца вектора 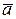 , взятое со знаком «+», если отрезок АВ ориентирован (считая от А к В) в положительную сторону оси l и знаком «-» – в противном случае (см. рис.2).
, взятое со знаком «+», если отрезок АВ ориентирован (считая от А к В) в положительную сторону оси l и знаком «-» – в противном случае (см. рис.2).
Обозначение: 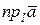 .
.
Теорема 1. Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и положительным направлением оси (рис. 3):
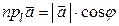 . (1)
. (1)
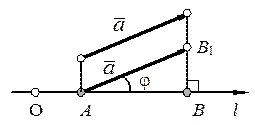 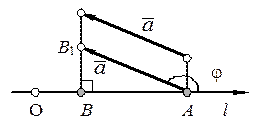 Рис.3. Рис.4. Рис.3. Рис.4. |
Доказательство. Из 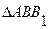 (рис. 3) получаем
(рис. 3) получаем 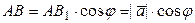 . Направление отрезка
. Направление отрезка 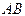 совпадает с положительным направлением оси
совпадает с положительным направлением оси 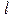 , поэтому справедливо равенство
, поэтому справедливо равенство 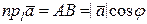 . В случае противоположной ориентации (рис.4) имеем
. В случае противоположной ориентации (рис.4) имеем 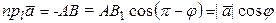 . Теорема доказана.
. Теорема доказана.
Рассмотрим свойства проекций.
Свойство 1. Проекция суммы двух векторов 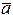 и
и 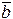 на ось равна сумме их проекций на ту же ось, то есть
на ось равна сумме их проекций на ту же ось, то есть 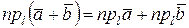 .
.
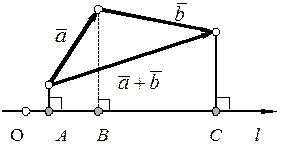 Рис.5. Рис.5. |
Доказательство в случае одного из возможных расположений векторов следует из рисунка 5. Действительно, по определению 2
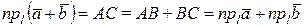 .
.
Свойство 1 справедливо для любого конечного числа слагаемых векторов.
Свойство 2. При умножении вектора на число l его проекция умножается на это число
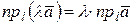 . (2)
. (2)
Докажем равенство (2). При 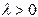 векторы
векторы 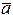 и
и 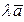 образуют с осью
образуют с осью 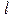 один и тот же угол. По теореме 1
один и тот же угол. По теореме 1
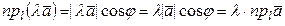
При 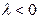 векторы
векторы 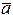 и
и 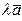 образуют с осью
образуют с осью 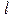 соответственно углы
соответственно углы 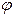 и
и 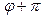 . Потеореме 1
. Потеореме 1
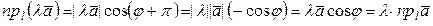 .
.
При 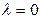 , получаем очевидное равенство
, получаем очевидное равенство
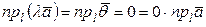 .
.
Следствие из свойств 1 и 2. Проекция линейной комбинации векторов равна такой же линейной комбинации проекций этих векторов, т.е.
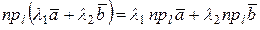 . (3)
. (3)
Тема 1. Матрицы и системы
Понятие матрицы
Определение 1. Матрицей размером 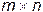 называется прямоугольная таблица чисел или буквенных выражений
называется прямоугольная таблица чисел или буквенных выражений 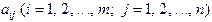 , записанных в виде
, записанных в виде

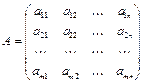 .
.
Здесь, aij (i=1,2,...,m; j=1,2,...n) - элементы матрицы, i- номер строки, j - номер столбца. Матрицы обычно обозначаются большими буквами латинского алфавита A, B, Cи т.д., а также 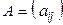 или
или 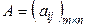 . При m=n матрица называется квадратной матрицей порядка n.
. При m=n матрица называется квадратной матрицей порядка n.
Квадратная матрица, у которой все элементы с неравными индексами i¹j равны нулю, называется диагональной:
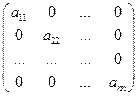
Если все отличные от нуля элементы диагональной матрицы равны единице, то матрица называется единичной. Единичную матрицу принято обозначать буквой E.
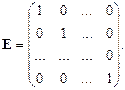
Матрица, все элементы которой равны нулю, называется нулевой и обозначается θ.
Существуют также матрицы, состоящие из одной строки или из одного столбца.
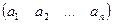 - матрица строка;
- матрица строка; 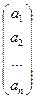 - матрица столбец.
- матрица столбец.
Числовой характеристикой квадратной матрицы является определитель (или детерминант).
Определители 2-го порядка и 3-го порядка, их свойства.
Определители 2-го порядка
Определение 2. Определителем второго порядка матрицы 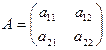 (или просто определителем второго порядка) называется число, обозначаемое символом
(или просто определителем второго порядка) называется число, обозначаемое символом 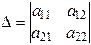 и определяемое равенством
и определяемое равенством 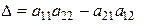 , то есть
, то есть
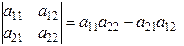 . (3)
. (3)
Другие обозначения: 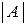 ,
, 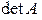 .
.
Таким образом, понятие определителя предполагает одновременно и способ его вычисления. Числа 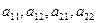 называются элементами определителя. Диагональ, образованная элементами
называются элементами определителя. Диагональ, образованная элементами 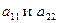 , называется главной, а элементами
, называется главной, а элементами 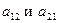 - побочной.
- побочной.
Пример 1. Определитель матрицы 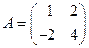 равен
равен
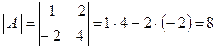 .
.
Определители 3-го порядка
Определение 2. Определителем третьего порядка называется число, обозначаемое символом
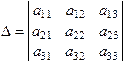 ,
,
и определяемое равенством
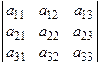 =
= 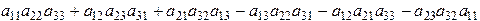 . (4)
. (4)
Числа 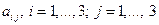 - элементы определителя. Элементы
- элементы определителя. Элементы 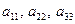 образуют главную диагональ, элементы
образуют главную диагональ, элементы 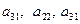 - побочную.
- побочную.
При вычислении определителя чтобы запомнить, какие слагаемые в правой части равенства (4) берутся со знаком «+», а какие со знаком «-», пользуются символическим правилом треугольников (правилом Саррюса):

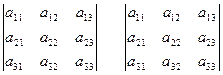
(+) (-)
Со знаком «+» берутся произведения элементов главной диагонали и элементов, находящихся в вершинах треугольников с основаниями, параллельными главной диагонали; сл знаком «-» – произведения элементов побочной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными побочной диагонали.
Вычисление определителя по правилу приписывания столбцов.
1. Приписываем справа от определителя последовательно первый и второй столбцы.
2. Вычисляем произведения трех элементов по диагонали слева - направо, сверху - вниз от а11 до а13 и берем их со знаком «+». Затем вычисляем произведения трех элементов по диагонали слева - направо, снизу вверх от а31 до а13 и берем их со знаком «-».

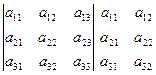
(-) (-) (-) (+) (+) (+)
Пример 2. Вычислить определитель 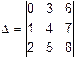 по правилу приписывания столбцов.
по правилу приписывания столбцов. 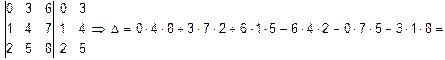
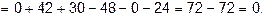
3. Определители n-ого порядка. Миноры и алгебраические дополнения. Вычисление определителей разложением по строке (столбцу).
Рассмотрим понятие определителя n-ного порядка. Определителем n-ного порядка называется число, сопоставляемое матрице n-ного порядка и вычисляемое по определенному закону.
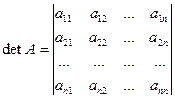 ,
,
здесь 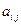 - элементы определителя. Чтобы показать правило, по которому раскрывается определитель n-ного порядка, рассмотрим некоторые понятия.
- элементы определителя. Чтобы показать правило, по которому раскрывается определитель n-ного порядка, рассмотрим некоторые понятия.
Определение 4. Минором 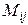 элемента
элемента 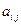 определителя n-го порядка называется определитель (n - 1) порядка, полученный вычеркиванием строки и столбца определителя, на пересечении которых расположен этот элемент.
определителя n-го порядка называется определитель (n - 1) порядка, полученный вычеркиванием строки и столбца определителя, на пересечении которых расположен этот элемент.
Определение 5. Алгебраическим дополнением 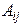 некоторого элемента
некоторого элемента 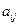 определителя n-го порядка называется минор этого элемента, умноженный на
определителя n-го порядка называется минор этого элемента, умноженный на 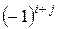 , то есть
, то есть 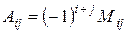 .
.
В определителе третьего порядка 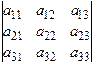 можно рассмотреть, например,
можно рассмотреть, например,
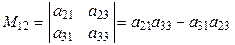 ,
, 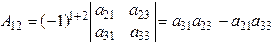 .
.
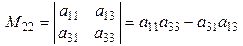 ,
, 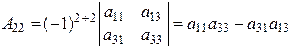 .
.
Определение 6.Определителем n-ного порядка называется число, равное сумме произведений элементов первой строки определителя, умноженных на их алгебраические дополнения.
Это правило вычисления определителя называется разложением по первой строке.
Теорема ( о разложении определителя). Определитель можно вычислить разложением по любой строке или столбцу.
– сумма произведений элементов 1-го столбца на алгебраические дополнения 2-го столбца.
Пример 3. Вычислить определитель четвертого порядка 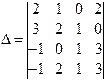 .
.
Решение. Умножаем третью строку на (-1) и прибавляем ее к четвертой, затем раскладываем определитель по четвертой строке:
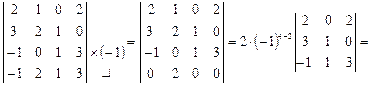
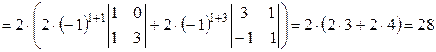 .
.
Определитель третьего порядка разложили по первой строке.
