Разбиения. Диаграммы Феррерса

Разбиение n-элементного множества X на k блоков — это семейство Q = {B₁, …, B_k}, в котором B₁ ∪ … ∪ B_k = X, B_i ∩ B_j = Ø, B_i ≠ Ø, для 1 ≤ i < j ≤ k. Обозначим множество всех разбиений множества X на k блоков через Π_k(X), а через Π(X) — множество всех разбиений.

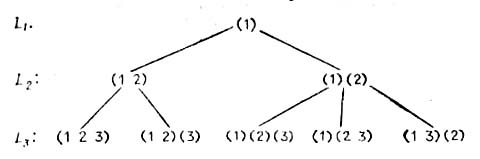
Довольно интересным является вопрос генерирования разбиений множества. Рассмотрим идею алгоритма, отвечающего на этот вопрос, описав ее в рекуррентной форме. Сначала сделаем ряд полезных замечаний. Можно показать, что разбиение Q множества {1, …, n} однозначно определяет разбиение Q_n−1 множества {1, …, n−1}, которое получается из Q после удаления элемента n (или пустого блока) из соответствующего блока. Также, если имеется разбиение W = {B₁, …, B_k} множества {1, …, n−1}, то можно отыскать все разбиения Q множества {1, …, n}, для которых Q_n−1 = W, т. е. такие разбиения:

B₁ ∪ {n}, …, B_k,
…
B₁, …, B_k ∪ {n},
B₁, …, B_k, {n}.

Обозначим такую последовательность через E. Тогда сформулируем несложный метод генерирования рабиений: если у нас есть список L_n−1 всех разбиений множества {1, …, n−1}, то список L_n разбиений множества {1, …, n} будем создавать, заменяя каждое разбиение Q в списке L_n−1 на соответствующую ему последовательность E. Проиллюстрируем построение списка L_n для n = 1, 2, 3.

Разбиение числа (натурального) n на k слагаемых — это последовательность a₁, …, a_k, такая что

n = a₁ + … + a_k, a₁ ≥ … ≥ a_k > 0.

Существует довольно простой способ представления разбиения числа — диаграмма Феррерса. Для разбиения a₁, …, a_k она состоит из k строк, которые соответствуют слагаемым разбиения, где i-я строка состоит из a_i точек. Сопряженное разбиение — это разбиение, получающееся при перемене ролями строк и столбцов в диаграмме Феррерса.

Производящая функция разбиений.

Разбие́ние числа́ n — это представление n в виде суммы положительных целых чисел, называемых частями. При этом порядок следования частей не учитывается (в отличие откомпозиций), то есть разбиения, отличающиеся только порядком частей, считаются равными. В канонической записи разбиения части перечисляются в невозрастающем порядке.

Производящая функция

Последовательность числа разбиений 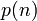имеет следующую производящую функцию:

Производящие функции разбиений на нечетные слагаемые,

на попарно неравные слагаемые. Доказать равенство этих производящих функций

разбиениями на нечётные слагаемые строится так:

Каждую часть разбиения нужно поделить на максимально возможную степень двойки. Частное будет нечётным числом и нужно включить это число в новое разбиение столько раз, каков делитель.

Класификация алгоритмов

Классификация алгоритмов сортировки

Количество алгоритмов сортировки достаточно велико. В книге Дональда Кнута "Искусство программирования для ЭВМ" рассматривается более двадцати (~25) алгоритмов сортировки. В настоящее время это число ещё больше увеличилось, и, вместе с экзотическими и мало распространёнными алгоритмами, приближается к 40 (и даже уже превышает 40, а с модификациями ещё больше, 42-44, скорее всего и эти цифры заниженные). Все эти алгоритмы можно классифицировать по нескольким признакам.

1. В зависимости от того, сортируются данные в оперативной памяти машины (ОЗУ) или во внешнем ЗУ, сортировка бывает внутренней или внешней.

2. В зависимости от того, какая структура данных подвергается сортировке, может быть сортировка бывает массива, связного списка, дерева (пирамиды), графа.

3. В зависимости от того, как структура данных меняется в процессе сортировки может быть сортировка списка (если элементы структуры данных перемещаются), или сортировка таблицы адресов (если элементы не перемещаются, а сортируется имеющаяся или создаваемая таблица адресов). В таблицу адресов могут быть добавлены ключи, тогда получается сортировка таблицы ключей.

4. По особенностям функциональной реализации алгоритмы сортировки делятся на группы:

Основные:
− сортировка перестановками (обменная);
− сортировка выбором (отбором);
− сортировка вставками;

Неосновные:
− сортировка подсчетом;
− сортировка слиянием;
− распределяющая сортировка.

5. По широте применения − универсальные (большинство перечисленных выше групп алгоритмов) и алгоритмы для конкретных случаев, не универсальные.

6. По признаку перестановки совпадающих данных в процессе сортировки − алгоритмы, не меняющие порядок следования совпадающих ключей (иногда такие алгоритмы не совсем удачно называют "устойчивыми" или "стабильными"), например, сортировка вставками, и меняющие порядок следования ("неустойчивые").

7. По характеру зависимости времени работы от размера N структуры данных:
− O(N²) − N‐квадратичные (это самые простые алгоритмы из 1-х трёх функциональных групп);
− O(N^k), где 1<k<2 (например, k = 1,6667 или k = 1,5 или k = 1,27 и т.п. − это алгоритм Шелла); возможен также случай, когда k = 3 − это один из самых неудачных и неэффективных алгоритмов, который получил название глупая сортировка (или дурацкая сортировка);
− O(log₂N) − логарифмические (например, быстрая сортировка или пирамидальная сортировка).

12.Сортировка методом хипа

Сортировка с помощью двоичного дерева (сортировка двоичным деревом, сортировка деревом, древесная сортировка, сортировка с помощью бинарного дерева, англ. tree sort) — универсальный алгоритм сортировки, заключающийся в построении двоичного дерева поиска по ключам массива (списка), с последующей сборкой результирующего массива путём обхода узлов построенного дерева в необходимом порядке следования ключей. Данная сортировка является оптимальной при получении данных путём непосредственного чтения с потока (например с файла, сокета или консоли).

Эффективность

Процедура добавления объекта в бинарное дерево имеет среднюю алгоритмическую сложность порядка O(log(n)). Соответственно, для n объектов сложность будет составлять O(n log(n)), что относит сортировку с помощью двоичного дерева к группе «быстрых сортировок». Однако, сложность добавления объекта в разбалансированное дерево может достигать O(n), что может привести к общей сложности порядка O(n²).

При физическом развёртывании древовидной структуры в памяти требуется не менее чем 4n ячеек дополнительной памяти (каждый узел должен содержать ссылки на элемент исходного массива, на родительский элемент, на левый и правый лист), однако, существуют способы уменьшить требуемую дополнительную память.

10) Двои́чная ку́ча, пирами́да[1], или сортиру́ющее де́рево — такое двоичное дерево, для которого выполнены три условия:

Значение в любой вершине не меньше, чем значения её потомков.

Глубина листьев (расстояние до корня) отличается не более чем на 1 слой.

Последний слой заполняется слева направо.

Если в куче изменяется один из элементов, то она может перестать удовлетворять свойству упорядоченности. Для восстановления этого свойства служит процедура Heapify. Она восстанавливает свойство кучи в дереве, у которого левое и правое поддеревья удовлетворяют ему. Эта процедура принимает на вход массив элементов A и индекс i. Она восстанавливает свойство упорядоченности во всём поддереве, корнем которого является элемент A[i].
Если i-й элемент больше, чем его сыновья, всё поддерево уже является кучей, и делать ничего не надо. В противном случае меняем местами i-й элемент с наибольшим из его сыновей, после чего выполняем Heapify для этого сына.

Построение кучи

Эта процедура предназначена для создания кучи из неупорядоченного массива входных данных.
Заметим, что если выполнить Heapify для всех элементов массива A, начиная с последнего и кончая первым, он станет кучей. В самом деле, легко доказать по индукции, что к моменту выполнения Heapify(A, i) все поддеревья, чьи корни имеют индекс больше i, кучи, и, следовательно, после выполнения Heapify(A, i) кучей будут все поддеревья, чьи корни имеют индекс, не меньший i.
Кроме того, Heapify(A,i) не делает ничего, если i>N/2 (при нумерации с первого элемента), где N — количество элементов массива. В самом деле, у таких элементов нет потомков, следовательно, соответствующие поддеревья уже являются кучами, так как содержат всего один элемент.
Таким образом, достаточно вызвать Heapify для всех элементов массива A, начиная (при нумерации с первого элемента) с -го и кончая первым.
Время работы равно .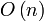

13) Двоичная сортировка (алгоритм Хоара).
Один из быстрых известных универсальных алгоритмов сортировки массивов.Другие названия этого алгоритма звучат как «быстрая сортировка» или «быстрая рекурсивная сортировка».

Выбираем в массиве некоторый элемент, который будем называть опорным элементом. С точки зрения корректности алгоритма выбор опорного элемента безразличен. С точки зрения повышения эффективности алгоритма выбираться должна медиана, но без дополнительных сведений о сортируемых данных её обычно невозможно получить. Известные стратегии: выбирать постоянно один и тот же элемент, например, средний или последний по положению; выбирать элемент со случайно выбранным индексом.

Операция разделения массива: реорганизуем массив таким образом, чтобы все элементы, меньшие или равные опорному элементу, оказались слева от него, а все элементы, большие опорного — справа от него. Обычный алгоритм операции:

Два индекса — l и r, приравниваются к минимальному и максимальному индексу разделяемого массива соответственно.

Вычисляется индекс опорного элемента m.

Индекс l последовательно увеличивается до тех пор, пока l-й элемент не превысит опорный.

Индекс r последовательно уменьшается до тех пор, пока r-й элемент не окажется меньше либо равен опорному.

Если r = l — найдена середина массива — операция разделения закончена, оба индекса указывают на опорный элемент.

Если l < r — найденную пару элементов нужно обменять местами и продолжить операцию разделения с тех значений l и r, которые были достигнуты. Следует учесть, что если какая-либо граница (l или r) дошла до опорного элемента, то при обмене значение m изменяется на r-й или l-й элемент соответственно.

Рекурсивно упорядочиваем подмассивы, лежащие слева и справа от опорного элемента.

Базой рекурсии являются наборы, состоящие из одного или двух элементов. Первый возвращается в исходном виде, во втором, при необходимости, сортировка сводится к перестановке двух элементов. Все такие отрезки уже упорядочены в процессе разделения.

17) СНИМОК

Отношение - это одна из форм всеобщей взаимосвязи всех предметов, явлений, процессов в природе, обществе и мышлении. Но, когда говорят об бинарных отношениях, то подразумевают отношения между двумя величинами, объектами, высказываниями.
Обычно отношения обозначают латинской буквой R.
Если хRх для любого х из поля отношения R то такое отношение называют рефлексивным, где х и х - объекты мысли , а R - это знак о том или ином виде отношения между объектами мысли.
Если хRу ® уRх, то такое отношение называется симметричным, где ® - знак импликации, сходный с союзом "! если..., то..."
Если (xRy Ùy R z) ® xRz, то такое отношение называется транзитивным, где Ù - знак конъюнкции.

Рефлексивность - это одно из свойств некоторых отношений, когда каждый элемент множества находится в данном отношении к самому себе. Например отношения между числами а = с и а ³ с рефлексивны, так как всегда а = а, с = с, а ³ а, с ³ с. Но отношение неравенства а > с антирефлексивно, так как неравенство а > а невозможно.
Аксиома рефлексивности записывается так: aRc ® aRa Ù cRc , здесь ® означает слово "влечёт" ("имплицирует"), а знак Ù - союз "и" (конъюнкция).
Из этой аксиомы следует: если суждение aRc истинно. то истинны и суждения aRa и cRc.
Симметричное отношение - это такое отношение между объектами, когда наличие этого отношения влечё за собой наличие этого отношения и в том случае, если объекты поменять местами; иначе говоря при счимметричном отношении перестановка объектов не ведёт к изменению вида отношения. Например, отношение равенства а = с симметрично, так как оно эквивалентно (равносильно) отношению с = а , си мметрично и отношение а ¹ с , так как оно эквивалентно отношению с ¹ а.
Транзитивное множество - это такое множество, например множдество х, если выполняется следующее требование: у Î х, z Î y ® z Î x где ® это знак, представляющий слова: " если ..., то ..." Читается формула так: Если у принадлежит х, z принадлежит у, то z принадлежит х".

19)Отношение эквивалентности ( ) на множестве — это бинарное отношение, для которого выполнены следующие условия:

1. Рефлексивность: для любого в ,

2. Симметричность: если , то ,

3. Транзитивность: если и , то .

20) Бинарное отношение 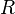на множестве 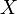называется отношением порядка, или отношением частичного порядка, если имеют место

• Рефлексивность:
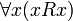
• Транзитивность: ;
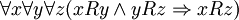• Антисимметричность: .

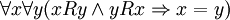21) Транзитивным замыканием 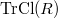отношения 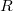на множестве 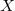называется пересечение всех транзитивных отношений, содержащих 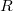как подмножество
Транзитивное замыкание существует для любого отношения. Для этого отметим, что пересечение любого множества транзитивных отношений транзитивно. Более того, обязательно существует транзитивное отношение, содержащее 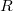как подмножество (например, ).
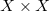Например, если 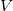- множество городов, и на них задано отношение 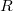, означающее, что если 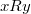, то "существует автобусный маршрут из x в y", то транзитивным замыканием этого отношения будет отношение "существует возможность добраться из x в y, передвигаясь на автобусах".

23)В комбинаторике размещением называется расположение «предметов» (объектов) на некоторых «местах» при условии, что каждое место занято в точности одним предметом и все предметы различны. Более формально, размеще́нием (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных же n элементов.
Количество размещений из n по k, обозначаемое 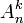, равно убывающему факториалу: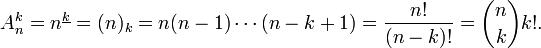
Последнее выражение имеет естественную комбинаторную интерпретацию: каждое размещение из n по k однозначно соответствует некоторому сочетанию из n по k и некоторойперестановке элементов этого сочетания; число сочетаний из n по k равно биномиальному коэффициенту 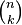, в то время как перестановок на k элементах ровно k! штук.
При k=n количество размещений равно количеству перестановок порядка n