Теорема 1. Всякую матрицу путем элементарных преобразований строк можно привести к ступенчатому виду

Институт сервиса, туризма и дизайна (филиал) в г. Пятигорске

Лекции по дисциплине «Алгебра»

Составитель: Чебоксаров А.Б.

Пятигорск 2015

Содержание

Раздел 1. Линейная алгебра.
Лекция 1. Матрицы.
Лекция 2. Определители.
Лекция 3. Системы линейных уравнений. Метод Гаусса решения систем.
Лекция 4. Другие методы решения систем линейных уравнений: матричный метод и метод Крамера.
Лекция 5. Условие совместности системы линейных уравнений. Общее решение однородной линейной системы.
Лекция 6,7. Линейные преобразования. Квадратичные формы.
Раздел 3. Комплексные числа.
Лекция 8. Понятие комплексных чисел. Действие с комплексными числами..
Лекция 9. Показательная форма комплексного числа. Разложение многочлена на множители.
Примерный перечень вопросов к экзамену

Раздел 1. Линейная алгебра.

Лекция 1. Матрицы.

Основные определения.

Определение. Матрицейразмера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются a_ij, где i- номер строки, а j- номер столбца.

А =

Основные действия над матрицами.

Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.

Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.

Определение. Матрица вида:

= E,

называется единичной матрицей.

Определение. Если a_mn = a_nm , то матрица называется симметрической.

Пример. - симметрическая матрица

Определение.Квадратная матрица вида называется диагональнойматрицей.

Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:

Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

c_ij = a_ij ± b_ij

С = А + В = В + А.

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

a (А+В) =aА ± aВ

А(a±b) = aА ± bА

Пример. Даны матрицы А = ; B = , найти 2А + В.

2А = , 2А + В = .

Операция умножения матриц.

Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:

A×B = C;

.

Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

Свойства операции умножения матриц.

1)Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.

Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.

Перестановочными могут быть только квадратные матрицы одного и того же порядка.

А×Е = Е×А = А

Очевидно, что для любых матриц выполняются следующее свойство:

A×O = O; O×A = O,

где О – нулеваяматрица.

2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:

(АВ)С=А(ВС).

3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:

А(В + С) = АВ + АС

(А + В)С = АС + ВС.

4) Если произведение АВ определено, то для любого числа a верно соотношение:

a(AB) = (aA)B = A(aB).

5) Если определено произведение АВ , то определено произведение В^ТА^Т и выполняется равенство:

(АВ)^Т = В^ТА^Т, где

индексом Т обозначается транспонированная матрица.

6) Заметим также, что для любых квадратных матриц det (AB) = detA×detB.

Понятие det (определитель, детерминант) будет рассмотрено ниже.

Определение. Матрицу В называют транспонированнойматрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.

А = ; В = А^Т= ;

другими словами, b_ji = a_ij.

В качестве следствия из предыдущего свойства (5) можно записать, что:

(ABC)^T = C^TB^TA^T,

при условии, что определено произведение матриц АВС.

Пример. Даны матрицы А = , В = , С = и число a = 2. Найти А^ТВ+aС.

A^T = ; A^TB = × = = ;

aC = ; А^ТВ+aС = + = .

Пример. Найти произведение матриц А = и В = .

АВ = × = .

ВА = × = 2×1 + 4×4 + 1×3 = 2 + 16 + 3 = 21.

Пример. Найти произведение матриц А= , В =

АВ = × = = .

Лекция 2. Определители.

Определители.( детерминанты).

Определение. Определителемквадратной матрицы А= 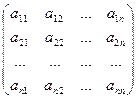называется число, которое может быть вычислено по элементам матрицы по формуле:

det A = , где

М_1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.

Предыдущая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:

det A =

Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:

detA = , i = 1,2,…,n.

Очевидно, что различные матрицы могут иметь одинаковые определители.

Определитель единичной матрицы равен 1.

Для указанной матрицы А число М_1к называется дополнительным минором элемента матрицы a_1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.

Определение. Дополнительный минор произвольного элемента квадратной матрицы a_ij равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.

Свойство1. Важным свойством определителей является следующее соотношение:

det A = det A^T;

Свойство 2. det (AB) = detA×detB

Свойство 3.Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.

Свойство 4. При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.

Определение: Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.

Свойство 6. Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.

Свойство 7. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)

Свойство 8. Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.

Свойство 9. Если для элементов какой- либо строки или столбца матрицы верно соотношение: d = d₁ ± d₂ , e = e₁ ± e₂ , f = f₁ ± f₂ , то верно:

Пример. Вычислить определитель матрицы А =

= -5 + 18 + 6 = 19.

Пример:. Даны матрицы А = , В = . Найти det (AB).

1-й способ: det A = 4 – 6 = -2; det B = 15 – 2 = 13; det (AB) = det A ×det B = -26.

2- й способ: AB = , det (AB) = 7×18 - 8×19 = 126 –

– 152 = -26.

Элементарные преобразования матрицы.

Определение. Элементарными преобразованиями матрицы назовем следующие преобразования:

1) умножение строки на число, отличное от нуля;

2) прибавление к элемнтам одной строки элементов другой строки;

3) перестановка строк;

4) вычеркивание (удаление) одной из одинаковых строк (столбцов);

5) транспонирование;

Те же операции, применяемые для столбцов, также называются элементарными преобразованиями.

С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк ( столбцов ).

Миноры.

Выше было использовано понятие дополнительного минора матрицы. Дадим определение минора матрицы.

Определение. Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется миноромматрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.

Заметим, что вышесказанное применимо не только к квадратным матрицам, но и к прямоугольным.

Если вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то определитель полученной матрицы будет являться дополнительным минором.

Алгебраические дополнения.

Определение. Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы.

В частном случае, алгебраическим дополнением элемента матрицы называется его дополнительный минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.

Теорема Лапласа. Если выбрано s строк матрицы с номерами i₁, … ,i_s, то определитель этой матрицы равен сумме произведений всех миноров, расположенных в выбранных строках на их алгебраические дополнения.

Обратная матрица.

Определим операцию деления матриц как операцию, обратную умножению.

Определение.Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,

где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратнойк матрице А и обозначается А^-1.

Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.

Рассмотрим общий подход к нахождению обратной матрицы.

Исходя из определения произведения матриц, можно записать:

AX = E Þ , i=(1,n), j=(1,n),

e_ij = 0, i ¹ j,

e_ij = 1, i = j .

Таким образом, получаем систему уравнений:

,

Решив эту систему, находим элементы матрицы Х.

Пример. Дана матрица А = , найти А^-1.

Таким образом, А^-1= .

Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:

,

где М_ji- дополнительный минор элемента а_ji матрицы А.

Пример. Дана матрица А = , найти А^-1.

det A = 4 - 6 = -2.

M₁₁=4; M₁₂= 3; M₂₁= 2; M₂₂=1

x₁₁= -2; x₁₂= 1; x₂₁= 3/2; x₂₂= -1/2

Таким образом, А^-1= .

Cвойства обратных матриц.

Укажем следующие свойства обратных матриц:

1) (A^-1)^-1 = A;

2) (AB)^-1 = B^-1A^-1

3) (A^T)^-1 = (A^-1)^T.

Пример. Дана матрица А = , найти А³.

А² = АА = = ; A³ = = .

Отметим, что матрицы и являются перестановочными.

Пример. Вычислить определитель .

= -1

= -1(6 – 4) – 1(9 – 1) + 2(12 – 2) = -2 – 8 + 20 = 10.

= = 2(0 – 2) – 1(0 – 6) = 2.

= = 2(-4) – 3(-6) = -8 + 18 = 10.

Значение определителя: -10 + 6 – 40 = -44.

Лекция 3. Системы линейных уравнений. Метод Гаусса решения систем.

Линейным уравнением с неизвестными х₁,x₂,…,x_n над полем К называется уравнение вида

a₁x₁+a₂x₂+…+a_nx_n=b

где коэффициенты a₁,a₂,…,a_n и свободный член b суть элементы поля К. Линейное уравнение называется однородным, если b = 0.

Система линейных уравнений с n неизвестными в общем виде записывается следующим образом:

. (3.1)

Матрица

называется матрицей коэффициентов, а матрица

A^*=

— расширенной матрицей системы (9.1).

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной — в противном случае. Совместная система может иметь одно или более решений. Решить систему уравнений — это значит найти все ее решения. Подчеркнем, что одно решение системы уравнений с n неизвестными — это упорядоченный набор из n чисел, т.е. элемент пространства Кⁿ.

Существует простой общий метод решения систем линейных уравнений, называемый методом Гаусса. Его идея состоит в приведении любой системы линейных уравнений с помощью некоторых специальных преобразований, называемых элементарными, к эквивалентной системе некоторого простого вида, все решения которой легко найти. Напомним, что две системы уравнений называются эквивалентными, если множества их решений совпадают, т. е. если каждое решение первой из них является решением второй, и наоборот.

Определение 1. Элементарными преобразованиями системы линейных уравнений называются преобразования следующих трех типов:

1) прибавление к одному уравнению другого, умноженного на число;

2) перестановка двух уравнений;

3) умножение одного уравнения на число, отличное от нуля.

Подчеркнем, что при элементарном преобразовании 1-го типа изменяется только одно уравнение — то, к которому прибавляется другое, умноженное на число.

Очевидно, что всякое решение исходной системы уравнений является решением новой системы, полученной элементарным преобразованием. С другой стороны, исходная система уравнений может быть получена из новой системы подходящим элементарным преобразованием того же типа. Так, если мы прибавим к первому уравнению второе, умноженное на с, то можно вернуться назад, прибавив к первому уравнению новой системы ее второе уравнение (которое такое же, как у исходной системы), умноженное на - с. Поэтому при любом элементарном преобразовании мы получаем систему уравнений, эквивалентную исходной.

Так как нам удобнее работать не с самими системами линейных уравнений, а с их (расширенными) матрицами, дадим соответствующее определение для матриц.

Определение 1'. Элементарными преобразованиями строк матрицы А называются преобразования следующих трех типов:

1) прибавление к одной строке другой, умноженной на число;

2) перестановка двух строк;

3) умножение одной строки на число, отличное от нуля.

Очевидно, что всякое элементарное преобразование системы линейных уравнений приводит к соответствующему элементарному преобразованию ее матрицы коэффициентов и расширенной матрицы.

Покажем теперь, что с помощью элементарных преобразований строк любую матрицу можно привести к достаточно простому виду. Назовем первый отличный от нуля элемент ненулевой строки (a₁,a₂,…,a_n) Кⁿ ее ведущим элементом.

Определение 2. Матрица называется ступенчатой, если

1) номера ведущих элементов ее ненулевых строк образуют строго возрастающую последовательность;

2) нулевые строки, если они есть, стоят в конце.

Таким образом, ступенчатая матрица — это матрица вида

(3.2)

в которой элементы a_1j1, а_2j2 ,…, a_rjr, находящиеся в углах ступенчатой линии, отличны от нуля, а все элементы, находящиеся слева и снизу от этой линии, равны нулю. При этом j₁<j₂<…<j_r.

Теорема 1. Всякую матрицу путем элементарных преобразований строк можно привести к ступенчатому виду.

Доказательство. Если данная матрица нулевая, то она уже ступенчатая. Если она ненулевая, то пусть j₁ — номер ее первого ненулевого столбца. Переставив, если нужно, строки, добьемся того, чтобы ≠ 0. После этого прибавим к каждой строке, начиная со второй, первую строку, умноженную на подходящее число, с таким расчетом, чтобы все элементы j₁ столбца, кроме первого, стали равными нулю. Мы получим матрицу вида

.

Поступая таким же образом с матрицей А₁, мы в конце концов получим матрицу вида (9.2). *

Замечание 1. В этом доказательстве мы обошлись без элементарных преобразований 3-го типа. Однако на практике они могут быть полезны.

Пример 1. Приведем к ступенчатому виду матрицу

Вычитая из 2-й, 3-й и 4-й строк 1-ю строку, умноженную на 1, 2 и 2 соответственно, получаем матрицу

Далее, прибавляя к 3-й и 4-й строкам 2-ю строку, умноженную на 3 и 4 соответственно, получаем матрицу

.

Наконец, переставляя 3-ю и 4-ю строки, получаем ступенчатую матрицу

.

Применим доказанную теорему к решению систем линейных уравнений.

Определение 3. Система линейных уравнений называется ступенчатой, если ее расширенная матрица ступенчатая.

Из теоремы следует, что всякую систему линейных уравнений с помощью элементарных преобразований можно привести к ступенчатому виду. Поэтому нам достаточно научиться решать ступенчатые системы.

Введем некоторую терминологию. Квадратная матрица А = (a_ij) называется треугольной, если а_ij = 0 при i > j, и строго треугольной, если, кроме того, а_ii ≠ 0 при всех i. Система линейных уравнений называется (строго) треугольной, если ее матрица коэффициентов (строго) треугольна.

Рассмотрим теперь произвольную ступенчатую систему линейных уравнений. Пусть число ненулевых строк (число ступенек) ее матрицы коэффициентов равно r, а число ненулевых строк расширенной матрицы равно p. Очевидно, что p = r или r+1.

Возможны следующие три принципиально разных случая.

1-й случай: p = r+1. В этом случае система содержит уравнение вида

0x₁+0x₂+…+0x_n=b

где b ≠ 0, и, следовательно, несовместна.

2-й случай: p = r = n. В этом случае после отбрасывания нулевых уравнений получается строго треугольная система. Из ее последнего уравнения однозначно определяется х_n, затем из предпоследнего уравнения — x_n-1 и т. д. Следовательно, система имеет единственное решение.

3-й случай: p = r < n. Пусть в этом случае j₁, j₂,…, j_r — номера ведущих коэффициентов ненулевых уравнений системы. Неизвестные назовем главными, а остальные — свободными. После отбрасывания нулевых уравнений и перенесения членов со свободными неизвестными в правую часть получается строго треугольная система относительно главных неизвестных. Решая ее, как в предыдущем случае, находим выражения главных неизвестных через свободные. Эти выражения называют общим решением системы. Все решения системы получаются из общего решения подстановкой каких-то значений свободных неизвестных. Поскольку эти значения могут выбираться произвольно, система имеет, во всяком случае, более одного решения, а если поле К бесконечно — то бесконечно много решений. Совместная система линейных уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае, как следует из проведенного выше анализа, она имеет бесконечно много решений, если только поле К бесконечно. Ее общее решение с точностью до перенумерации неизвестных имеет вид

. (3.3)

Пример 2. Решим систему уравнений

,

расширенной матрицей которой служит матрица из примера 1. Вычисления, проведенные в примере 1, показывают, что данная система эквивалентна ступенчатой системе

.

Считая неизвестные х₁, х₂, х₄ главными, а неизвестное х₃ свободным, перепишем систему в виде

Решая ее относительно х₁, х₂ , х₄, находим общее решение

.

Замечание 2. Для единообразия можно считать, что в случае определенной системы все неизвестные являются главными, а свободные неизвестные отсутствуют. Общее решение есть тогда единственное решение системы.

Замечание 3. Строго треугольную матрицу можно путем элементарных преобразований строк привести к единичной матрице. Для этого нужно сначала к каждой строке, кроме последней, прибавить последнюю строку с таким коэффициентом, чтобы элемент последнего столбца стал равным нулю, затем аналогичным образом, прибавляя предпоследнюю строку, сделать равными нулю все элементы предпоследнего столбца, кроме диагонального, и т. д. В результате мы получим диагональную матрицу. Умножая ее строки на подходящие числа, мы получим единичную матрицу. Пользуясь этим, можно при решении системы линейных уравнений не останавливаться на ступенчатом виде, а, продолжив преобразования, привести матрицу коэффициентов при главных неизвестных к единичной матрице. Тогда общее решение просто считывается с полученной матрицы. Эта процедура называется обратным ходом метода Гаусса.

Система однородных линейных уравнений всегда совместна, так как она имеет нулевое решение. Если она определенна, то она имеет только нулевое решение, если неопределенна — то имеет хотя бы одно ненулевое решение (и даже бесконечно много таких решений, если поле К бесконечно). В предыдущих обозначениях, последний случай имеет место, если r < n. Пользуясь тем, что всегда r ≤ m, мы приходим к следующей теореме, которая является важным теоретическим следствием метода Гаусса.