Метод замены плоскостей проекций
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
РОССИИ
ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
МИАССКИЙ ФИЛИАЛ
МАШИНОСТРОИТЕЛЬНЫЙ ФИЛИАЛ
БЕРЕЖКО Л.Н.
МЕТОДИЧЕСКОЕ ПОСОБИЕ
Для студентов очной формы обучения
По выполнению заданий №2 и 3
ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Тема «Поверхности»
Миасс,2007
СОДЕРЖАНИЕ
СОДЕРЖАНИЕ.. 2
ВВЕДЕНИЕ.. 3
1.РЕШЕНИЕ ЗАДАНИЯ №3. 4
1.1 Метод замены плоскостей проекций. 4
1.2. Преобразование плоскости общего положения в проецирующую плоскость. 6
1.3. Преобразование поверхности. 7
1.4. Построение линии пересечения поверхности проецирующими плоскостями. 10
1.4.1.Сечение призмы проецирующей плоскостью.. 11
1.4.2.Сечение пирамиды проецирующей плоскостью.. 11
1.4.3. Сечение цилиндра проецирующей плоскостью.. 11
1.4.4. Сечение конуса проецирующей плоскостью.. 12
1.4.5. Сечение сферы проецирующей плоскостью.. 14
1.5. Построение линии пересечения геометрического тела плоскостью.. 15
1.6. Построение натурального вида сечения. 16
2. РЕШЕНИЕ ЗАДАДАНИЯ № 4. 18
2.1. Пересечение поверхностей. 18
2.1.1. Пересечение поверхностей, одна из которых занимает простейшее положение. 19
2.1.2.Метод вспомогательных секущих плоскостей. 20
2.1.3. Метод вспомогательных концентрических сфер. 23
2.1.4. Заключение по первой части задания №4. 26
2.2. Построение разверток поверхностей. 27
2.2.1. Развертка призмы.. 27
2.2.2. Развертка пирамиды.. 28
2.2.3. Развертка цилиндра. 32
2.2.4. Развертка конуса. 33
ЗАКЛЮЧЕНИЕ.. 35
ВВЕДЕНИЕ
Контрольные задания № 3и4 по начертательной геометрии выполняются студентами после изучения следующих тем:
1.Методы преобразования проекций. Замена плоскостей проекций.
2.Сечение поверхности проецирующими плоскостями.
3.Взаимное пересечение поверхностей.
Изучение этих тем позволит выполнить контрольные задания без особых усилий, так как в основе решения задач лежит материал, изложенный в этих темах. Кроме того, желательно ознакомиться с методическими указаниями по решению метрических задач методом замены плоскостей проекций, имеющихся на кафедре технической механики.
В данном методическом пособии рассмотрен порядок выполнения контрольных заданий с изложением основного теоретического материала, знание которого необходимо для решения задач.
РЕШЕНИЕ ЗАДАНИЯ №2
Условие задачи сформулировано следующим образом.
Даны: непрозрачное геометрическое тело и секущая плоскость, заданная двумя пересекающимися прямыми.
Требуется на комплексном чертеже:
1.Построить проекции линии пересечения поверхности геометрического тела плоскостью.
2.Определить видимость элементов геометрического тела и линии сечения.
3.Построить истинный вид сечения.
Варианты задач представлены в методических указаниях.
Геометрическое тело представляет собой совокупность нескольких поверхностей, например, цилиндр и конус или призма, в основании которой лежит правильный пятиугольник, и конус, который стоит на этой призме.
Секущая плоскость задана двумя пересекающимися прямыми и является плоскостью общего положения. Решение задачи сводится к построению линии пересечения этих поверхностей плоскостью общего положения. В общем виде построение линии пересечения поверхности плоскостью общего положения решается довольно сложно. Особенно это касается таких поверхностей как пирамида, конус и сфера.
Но если плоскость занимает проецирующее положение, то решение задачи по построению линии пересечения поверхности такой плоскостью значительно упрощается.
Следовательно, решение задачи удобно проводить после преобразования плоскости общего положения в проецирующую, т.е. перпендикулярную одной из плоскостей проекций. Это преобразование проведем с помощью метода замены плоскостей проекций.
Разберем основы этого метода в следующем подразделе.
Метод замены плоскостей проекций
Сущность этого метода заключается в том, что при неизменном положении геометрических тел в пространстве плоскости проекций поочередно заменяются таким образом, чтобы эти тела заняли по отношению к новым плоскостям частное положение.
Для выяснения основных принципов метода замены плоскостей проекций рассмотрим преобразование чертежа для точки.
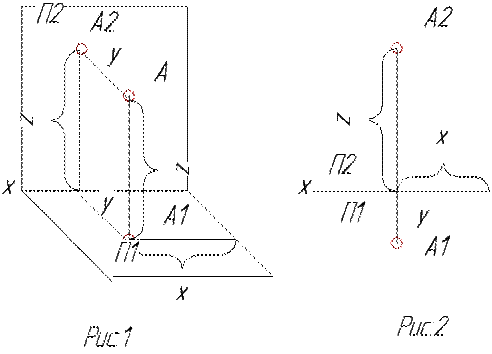
Пусть дана система плоскостей проекций П1 и П2, где П1- это горизонтальная плоскость проекций и П2- фронтальная плоскость проекций. В этой системе плоскостей задана точка А, которая спроецирована на эти плоскости и получены проекции точки А – А1- горизонтальная проекция и А2- фронтальная проекция (рис.1).
На рисунке 2 показан комплексный чертеж точки А.
На пространственном чертеже вместо плоскости П 2 введем новую плоскость проекций П4. Эта плоскость перпендикулярна горизонтальной плоскости проекций П1 и образует с ней новую систему плоскостей проекций П1-П4.Положение самой точки А осталось неизменным, т.е. сохранилось её расстояние до плоскости проекций П1.Это обстоятельство используем для построения проекций точки А в новой системе плоскостей проекций (рис.3, 4) .
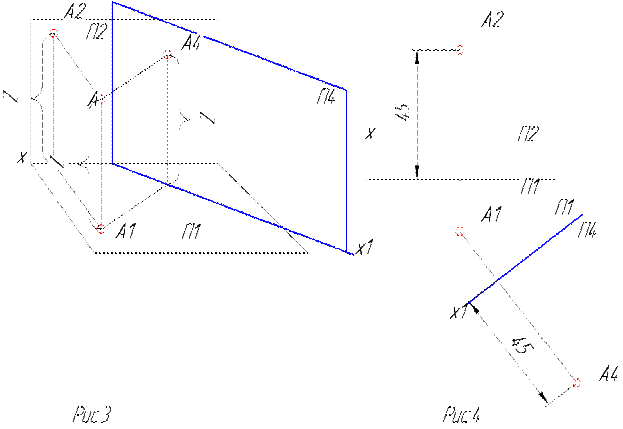
При замене плоскостей П2 на П4 положение горизонтальной проекции точки А (А1) остается неизменной, появляется новая проекция точки на плоскость П4 (А4), которую можно построить, используя расстояние от проекции А2 до оси Х1.Для этого от горизонтальной проекции А1 проводим перпендикуляр к оси Х2 . На этом перпендикуляре от оси Х2 откладываем расстояние от А2 до оси Х1. Получаем новую фронтальную проекцию точки А.
