Метод замены плоскостей проекций.

МЕТОД ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Изменение взаимного положения изучаемого объекта и плоскостей проекций достигается путем замены одной из плоскостей П₁ или П₂ новой плоскостями П₄ (рис. 148). Новая плоскость всегда выбирается перпендикулярно оставшейся плоскости проекций.

Для решения некоторых задач может потребоваться двойная замены плоскостей проекций (рис. 149). Последовательный переход от одной системы плоскостей проекций к другой необходимо осуществлять, выполняя следующее правило: расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до заменяемой оси.

Задача 1: Определить натуральную величину отрезка АВ прямой общего положений (рис. 148). Из свойства параллельного проецирования известно, что отрезок проецируется на плоскость в натуральную величину, если он параллелен этой плоскости.

Выберем новую плоскость проекций П₄, параллельно отрезку АВ и перпендикулярно плоскости П₁. Введением новой плоскости, переходим из системы плоскостей П₁П₂ в систему П₁П₄ , причем в новой системе плоскостей проекция отрезка А₄ В₄ будет натуральной величиной отрезка АВ.

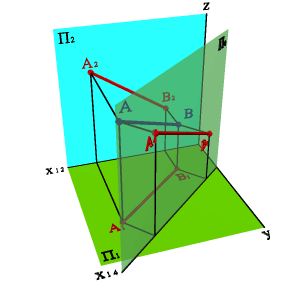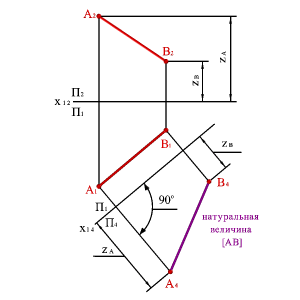а) модель	б) эпюр
Рисунок 148. Определение натуральной величины отрезка прямой методом замены плоскостей проекций

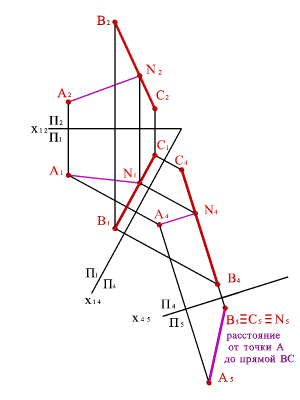
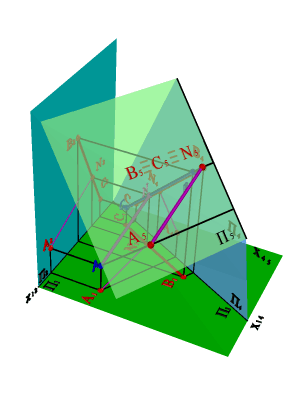
Задача 2: Определить расстояние от точки А до прямой общего положения, заданной отрезком ВС (рис._149).

Понятие многогранника.

Многогранники – замкнутые пространственные фигуры, ограниченные плоскими многоугольниками. Вершины и стороны многогранников являются вершинами и ребрами многогранников. Они образуют пространственную сетку. Если вершины и ребра многогранника находятся по одну сторону плоскости любой из его граней, то многогранник называют выпуклым, все его грани – выпуклые.

Из всего многообразия многогранников наибольший практический интерес представляют призмы, пирамиды, правильные многогранники и их разновидности.

Многогранник, две грани которого n-угольники в параллельных плоскостях, а остальные n-граней - параллелограммы, называется n-угольной призмой. Многогранники являются основаниями призмы, а параллелограммы – боковыми гранями призмы.

Многогранник, у которого одна из граней – произвольный многоугольник, а остальные грани – треугольники, имеющие общую вершину, называются пирамидой. Грань–многоугольник называют основанием призмы, а треугольники – боковыми гранями пирамиды. Общая вершина треугольников называется особой вершиной пирамиды (обычно, просто вершиной).

Если пирамиду отсечь плоскостью параллельной основанию, то получим усеченную пирамиду.

Многогранник называется метрически правильным, если все его грани являются правильными многоугольниками. К ним относятся куб, тетраэдр, октаэдр, икосаэдр, додекаэдр.

Под изображением многогранников на чертеже будем понимать изображение ограничивающей его многогранной поверхности, т.е. изображение совокупности составляющих ее многогранников. Графически простую многогранную поверхность удобно задавать проекциями ее сетки.

Построение проекций:

Построение проекций многогранников

Построение проекции многогранника на некоторой плоскости сводится к построению проекций точек. Например, проецируя пирамиду SABC на пл.я₂ (рис. 256, слева), мы строим проекции вершин S, А, В и С и, как следствие, проекции основания ABC, граней SAB, SBC, SAC, ребер SA, SB и др.

Также, проецируя трехгранный угол ') с вершиной S (рис. 256, справа), мы, помимо вершины S, берем на ребрах угла по одной точке (К, М, N) и проецируем их

на пл. я₂; в результате получаем проекции ребер и граней (плоских углов) трехгранного угла и В целом самый угол.

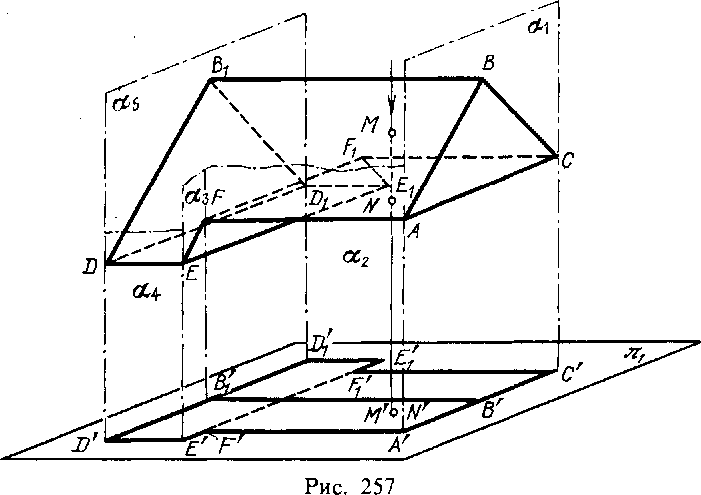
На рис. 257 изображены многогранное тело ACBB₁D... (т. е. часть пространства, ограниченного со всех сторон плоскими фигурами — многоугольниками) и его проекция на пл. я₁ — фигура A'C'F [E[DID'E'F'. Каждая точка, расположенная внутри очерка этой фигуры (т. е. линии, ограничивающей ее), является проекцией по крайней мере двух точек поверхности этого тела. Например, точка с двойным обозначением М' и N' служит проекцией точек М и N, лежащих на общей для них проецирующей прямой.

Точка, лежащая на самом очерке проекции, является проекцией или одной точки (например, А' есть проекция точки А), или нескольких, а иногда и множества точек (например, В' является проекцией не только точки В, но и множества точек грани ABC, расположенных на проецирующей прямой В В').

Проецирующие прямые, проходящие через все точки очерка проекции, в своей совокупности образуют проецирующую поверхность, внутри которой, касаясь ее, заключено данное тело. Для тела, изображенного на рис. 257, проецирующая поверхность состоит из плоскостей о^, а₂, а₃ и т. д. Линия касания проецирующей поверх-

') В данном случае выпуклый, т. е. такой, который весь расположен по одну сторону от плоскости каждой из его граней, неограниченно продолженной.

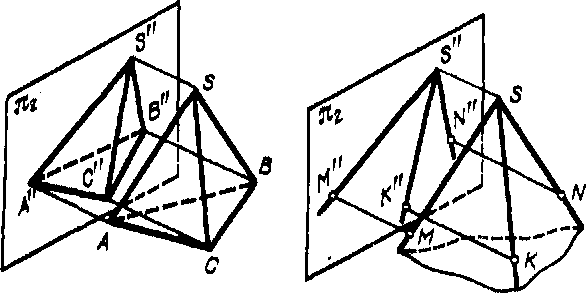
Рис. 256

Рис. 256

ности и тела называется контуром тела по отношению к выбранной плоскости проекций. На рис. 257 таким контуром служит ломаная ACF₁E₁D₁DEFA ¹).

Проецирующей поверхностью при параллельном проецировании является, как это указывалось в § 1, поверхность цилиндрическая. Если контур тела по отношению к плоскости проекций содержит прямолинейные отрезки, то проецирующая поверхность для каждого такого участка обращается в плоскую.

Проведенная на проекции прямая В'В{ является проекцией ребра BB_V видимого по отношению к пл. п₁. Показ на проекции тела всех видимых его ребер является обязательным.

Проекция отрезка FF₁ получается внутри очерка проекции; она показана штриховой линией, так как, по условиям видимости, точки отрезка FF_i при проецировании на пл. невидимы.

Построение проекции гранной поверхности также сводится к построению проекций некоторых точек и прямых линий этой поверхности. Проекция поверхности, ограничивающей какое-либо тело, имеет очерк, общий с очерком проекции этого тела. В случае изображения бесконечно простирающейся поверхности отделяют линиями некоторую ее часть и тем устанавливают условный контур по отношению к плоскости проекций.

Многогранник называется правильным, если его грани - правильные многоугольники, причем в каждой его вершине сходится равное число таких многоугольников.

Заметим, что число многоугольников, сходящихся в одной вершине - 3 или больше. Возьмем три пятиугольника - они действительно образуют уголок "шапочку". Три шестиугольника уже лежат в плоскости, а вот три семиугольника - не влезут. =>грани правильных многогранников не более, чем шести угольны. Т.е. правильный многогранник может быть с гранями треугольными, квадратными и пятиугольными. Причем в одной вершине может сходиться три квадрата или три пятиугольника, или три, четыре или пять треугольников.

Вариант первый. Грани многогранника - квадраты (в каждой вершине сходится три квадрата). Пусть число вершин такого многогранника - В. => число граней 3В/4. Заметим, что в каждой вершине ребер сходится столько же, сколько и граней. Число ребер такого многогранника 3В/2. Мы знаем, что В+Г-Р=2. Составим уравнение: В+3/4 В-3/2 В=2. В=8. Т.е. у такого многогранника 8 вершин, 6 граней и 12 ребер. Т.е. это куб.

Вариант второй. Грани многогранника правильные пятиугольники (в каждой вершине сходится по три пятиугольника). Г=3В/5. Р=3В/2. В+Г-Р=2. В=20. Г=12. Р=30. Это додекаэдр.

Вариант третий. Треугольники, по три. Г=3В/3=В. Р=3В/2. =>В=4=Г, Р=6. Это тетраэдр.

Вариант четвертый. Треугольники, по четыре. Г=4В/3, Р=4В/2=2В. => В=6, Г=8, Р=12. Это октаэдр.

Вариант пятый. Треугольники, по пять. Г=5В/3, Р=5В/2 => В=12, Г=20, Р=30. Это икосаэдр.

Других правильных многогранников нет.

Поверхности.

КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ

В зависимости от формы образующей и закона ее перемещения в пространстве поверхности можно разделить на отдельные группы, которые указаны на рис.3.4.
Линейчатые поверхности - поверхности, которые могут быть образованы с помощью прямой линии.
Нелинейчатые поверхности - поверхности, которые могут быть образованы только с помощью кривой линии.
Развертывающиеся поверхности - поверхности, которые после разреза их по образующей могут быть совмещены с плоскостью без наличия разрывов и складок.
Неразвертывающиеся поверхности - поверхности, которые не могут быть совмещены с плоскостью без наличия разрывов и складок.
Поверхности с постоянной образующей - поверхности, образующая которых не изменяет своей формы в процессе образования поверхности.
Поверхности с переменной образующей - поверхности, образующая которых изменяется в процессе образования поверхности.

Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственной кривой). Например, если прямая пересекает ось вращения, то при её вращении получитсяконическая поверхность, если параллельна оси — цилиндрическая, если скрещивается с осью — однополостный гиперболоид вращения. Одна и та же поверхность может быть получена вращением самых разнообразных кривых.

Примеры:

Сфера (получается вращением окружности вокруг оси, лежащей в той же плоскости и проходящей через её центр).

Тор (получается вращением окружности вокруг не пересекающей её оси, лежащей в той же плоскости).

Эллипсоид вращения ― эллипсоид, длины двух полуосей которого совпадают. Может быть получен вращением эллипсавокруг одной из его осей.

Параболоид вращения ― эллиптический параболоид, полученный вращением параболы вокруг своей оси.

Конус получается вращением прямой вокруг другой прямой, пересекающей первую.

Круговая цилиндрическая поверхность

Катеноид

"Поверхность, одно из основных геометрических понятий. При логическом уточнении этого понятия в разных отделах геометрии ему придаётся различный смысл.

Математически строгое определение поверхности основывается на понятиях топологии. При этом основным является понятие простой поверхности, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и изгибаниям)

Если же группировать поверхности по закону движения образующей линии и производящей поверхности, то большинство встречающихся в технике поверхностей можно разделить на:

• Поверхности вращения;

• Винтовые поверхности;

• Поверхности с плоскостью параллелизма;

• Поверхности переноса.

Поверхности вращения – это поверхности созданные при вращении образующей m вокруг оси i

Винтовые поверхности образуются винтовым движением некоторой линии – образующей.

Поверхность с плоскостью параллелизма представляет собой множество прямых линий l (образующих), параллельных некоторой плоскости ? (плоскости параллелизма) и пересекающих две данные направляющие m, n

Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным перемещением образующей - плоской кривой линии m по криволинейной направляющей n

20-22. Пересечение многогранником плоскостью.

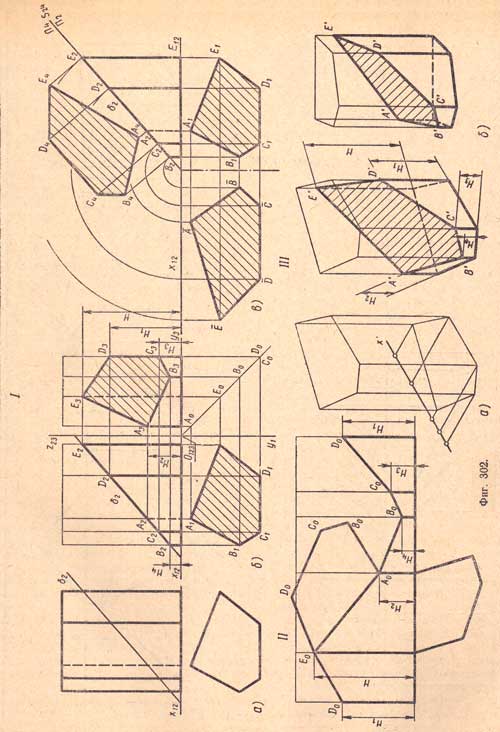
I, а. Треугольная прямая призма поставлена основанием на плоскость П₁ и рассечена плоскостью а общего положения.
Требуется:
а) построить проекции сечения;
б) найти натуральную величину фигуры сечения;
в) построить развертку поверхности усеченной призмы;
г) построить аксонометрическую проекцию усеченной призмы.
В этом случае горизонтальная проекция фигуры сечения сливается с горизонтальной проекцией призмы, так как боковые ребра и грани призмы перпендикулярны плоскости П₁. Для построения фронтальной проекции воспользуемся горизонталями. Через точку А₁ - горизонтальную проекцию ребра - проводим прямую, параллельную проекции следа k₁ - горизонтальную проекцию h₁ горизонтали. Затем найдем ее фронтальную проекцию h₂, которая, пересекаясь с фронтальной проекцией ребраD₂E₂ в точке А₂определит фронтальную проекцию точки пересечения ребра призмы с плоскостью а.
I, б. Аналогичным построением находим остальные точки пересечения ребер призмы плоскостью а (В₂, С₂), после чего соединим последовательно прямыми точки А₂, В₂, С₂ и А₂ и получим фронтальную проекцию А₂В₂С₂фигуры сечения - треугольника.
I, в. Натуральную величину фигуры сечения находим путем совмещения плоскости а с плоскостью П₁ вращением вокруг проекции следаk₁
II и III. Построение развертки поверхности усеченной призмы и аксонометрических проекций аналогично соответствующим построениям для пятиугольной призмы

МЕТОД СФЕР

Способ сфер можно применять при определенных условиях:

1)пересекающиеся поверхности должны быть поверхностями вращения

2)пересекающиеся поверхности должны иметь общую плоскость симметрии, || плоскости проекций, при этом, если оси вращения поверхностей пересекаются, то для определения точек линий пересечения поверхностей применяют вспомогателные концентрические сферы.

Если оси проекции сферы скрещивающиеся то применяют способ эксцентрических сфер.

Вспомогательные сферы с мин. радиусом должна вписываться в одну поверхность и пересекать другую одновременно.

Чтобы определить радиус сферы из точки пересечения осей проводят нормаль к поверхности ( | к образущей)

Большую из нормалей принимают за радиус минимальной сферы.

Для определения центра вспомогательной сферы на одной из поверхностей выделяют окружность, из центра отой окружности проводят |, отмечают точку пересечения проведенного | с осью вращения воторой поверхности, эту точку и принимают за центр вспомогательной сферы.

Способ секущих плоскостей

Линией пересечения поверхностей называют такую линию, точки которой одновременно принадлежат обеим поверхностям.

Для того, чтобы провести проекции линии пересечения поверхностей необходимо сначала определить множество точек, принадлежащих обеим поверхностям и затем соединить их плавной линией.

Точки, принадлежащие линии пересечения поверхностей определяют по след-му алгоритму:

1)вводят вспомогательную поверхность пересекающую обе заданных поверхностей (желательно по графически простым линиям)

2)определяют проекции линий пересечения вспомогательной поверхности с каждой их хаданных

3)отмечают точки пересечения, построенных линий пересечения

эти точки и будут общими для обеих заданных поверхностей и следовательно принадлежать их линии пересечения.

ПЕРЕСЕЧЕНИЕ ТЕЛ ВРАЩЕНИЯ