Раздел 4. Математико-статистические методы обработки исследовательского материала
Наиболее доступными и простыми способами математической обработки являются: вычисление средней арифметической Хср., среднего квадратичного отклонения -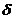 
, ошибки среднего арифметического - Sx, достоверности различий между двумя средними величинами t разл.
Среднее арифметическое вычисляется по формуле:
,
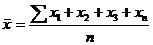где Х - среднее арифметическое,
Σ - сумма,
х1, х2, х3,… х n - показатели подготовленности испытуемых в исследуемой группе,
n – количество испытуемых.
Например, при измерении частоты сердечных сокращений (ЧСС) в группе детей 12-13 лет были получены следующие результаты:
| № п\п | Ф.И.О. исследуемого | Результат исследования (ЧСС, уд \ мин) | |
| Иванов. П | Х1 | ||
| Петров В. | Х2 | ||
| Сидоров В. | Х3 | ||
| Купцов М. | Х4 | ||
| Сидорчук К. | Х5 |
В данной группе n составляет 5 единиц (n = 5). Из таблицы видно, что в изучаемой группе наблюдается варьирование пульса (изменение в определенных пределах) – от 74 уд\мин до 80 уд\мин.
Подставив значения в формулу, получим следующий результат:
_
Х =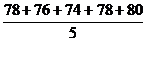 
= 77,2
Искомое среднее арифметическое исследуемой группы (n = 5) будет составлять 77, 2 уд\мин.
Необходимо заметить, что при оценке полученных данных значение среднего арифметического не даёт полной информации о варьирующем признаке. Поэтому наряду со средними значениями вычисляют и характеристики рассеяния выборки.
Среднее квадратическое отклонение вычисляется по формуле:
,
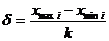где Хmaxi - наибольший показатель в исследуемой группе,
Хmini – наименьший показатель в группе,
К – коэффициент, зависящий от количества испытуемых в группе (С.И.Ермолова).
Таблица 1.
Коэффициент К для разных значений n
| - | - | 1,13 | 1,69 | 2,06 | 2,33 | 2,53 | 2,70 | 2,85 | 2,97 | |
| 3,08 | 3,17 | 3,26 | 3,34 | 3,41 | 3,47 | 3,53 | 3,59 | 3,64 | 3,69 | |
| 3,73 | 3,78 | 3,82 | 3,86 | 3,90 | 3,93 | 3,96 | 4,00 | 4,03 | 4,06 | |
| 4,09 | 4,11 | 4,14 | 4,16 | 4,19 | 4,21 | 4,24 | 4,26 | 4,26 | 4,30 | |
| 4,32 | 4,34 | 4,36 | 4,38 | 4,40 | 4,42 | 4,43 | 4,45 | 4,47 | 4,48 | |
| 4,50 | 4,51 | 4,53 | 4,54 | 4,56 | 4,57 | 4,59 | 4,60 | 4,61 | 4,63 | |
| 4,64 | 4,66 | 4,66 | 4,68 | 4,69 | 4,70 | 4,71 | 4,72 | 4,73 | 4,74 | |
| 4,75 | 4,77 | 4,78 | 4,79 | 4,80 | 4,81 | 4,82 | 4,83 | 4,83 | 4,84 | |
| 4,85 | 4,86 | 4,87 | 4,88 | 4,89 | 4,90 | 4,91 | 4,91 | 4,92 | 4,93 | |
| 4,94 | 4,95 | 4,96 | 4,97 | 4,97 | 4,98 | 4,99 | 4,99 | 5,00 | 5,01 | |
| N | ||||||||||
| К | 5,02 | 5,49 | 5,76 | 5,96 | 6,07 | 6,18 | 6,28 | 6,35 | 6,42 | 6,48 |
Пределы колебаний средней арифметической, ошибка средней арифметической вычисляются по формуле:
,
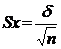где: Sx - пределы колебаний,
n – количество испытуемых,
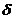- среднее квадратическое отклонение
Коэффициент вариативности:
,
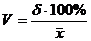где: 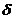- среднее квадратическое отклонение,
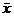– среднее арифметическое.
Различия в показателях подготовленности учащихся в динамике обследования, под воздействием эксперимента определяется по формуле:
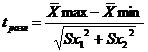
где tразл. – степень различия в показателях,
Хmaxi – больший средний показатель в исследуемой группе,
Хmini - меньший средний показатель в исследуемой группе,
Sx1, Sx2 -ошибка среднего арифметического.
При условии, что t разл.› 2,0 различия в средних показателях за период эксперимента статистически достоверны, при меньших значениях – или имеют тенденцию к достоверности, или не достоверны.
Достоверность различий часто демонстрируется процентным распределением вероятности Р со знаком ‹ или › и определяется значениями Р‹0,05; Р‹0,01; Р‹0,001, что соответствует достоверности факта полученного результата в 95% случаев; 99,0% случаев и 99,9% случаев при проведении аналогичного эксперимента с другим контингентом испытуемых.
Более подробно методика математико-статистической обработки изложена:
1. Ашмарин Б.А. Теория и методика педагогических исследований в физическом воспитании /Б.А. Ашмарин - М.: ФиС. - 1978. -С.160-190.
2. Годик М.А. Спортивная метрология /М.А. Годик - М.: ФиС. - 1988. - 192 с.
3. Начинская С.В. Основы спортивной статистики /С.В. Начинская - К.: Вища школа. - 1987. -187 с.
Раздел 5. Требования к оформлению таблиц и рисунков
Все таблицы нумеруют арабскими цифрами. Если таблица располагается в тексте работы, то ее номер ставится исходя из номера раздела работы, в котором таблица находится и порядкового номера таблицы в пределах раздела, разделенных точкой.
Перед названием таблицы справа печатается слово «Таблица». Например: Таблица 2.1. – первая таблица второго раздела.
Если таблица располагается на нескольких страницах, слово «Таблица», номер таблицы и её заголовок указывается один раз сверху над первой частью таблицы; над другими частями таблицы пишется «Продолжение таблицы» с указанием её номера, но без заголовка.
Заголовки граф таблицы печатают с прописных букв, а подзаголовки со строчных, если они составляют одно предложение с заголовком. Подзаголовки, имеющие самостоятельное значение, печатают с прописных букв. В конце заголовков и подразделов таблиц точки не ставят.
Пример оформления таблицы – приложение 4.
Оформление рисунков.
Иллюстрациями называют рисунки, схемы, графики, диаграммы, фотоснимки.
Иллюстрации располагают в работе непосредственно после первого упоминания в тексте. Допускается располагать на одном листе несколько иллюстраций.
Все иллюстрации необходимо нумеровать арабскими цифрами. Если иллюстрация размещена в тексте работы, то её номер состоит из номера раздела, в котором иллюстрация находится и порядкового номера иллюстрации в пределах раздела, разделенных точкой. Перед номером иллюстрации печатается слово «Рис.».
Все иллюстрации должны иметь название, которое размещается под ней после слова «Рисунок» и номера иллюстрации.
Если на иллюстрации встречаются схематические изображения, сокращения, то после ее названия помещают поясняющие данные (под рисуночный текст).
При ссылке в работе на таблицу пишут следующим образом: «…в таблице 1.3. показано…».
При ссылке в работе на рисунок или иллюстрацию пишут следующим образом: «…на рисунке 1.3. показано…».
При ссылке в работе на приложение пишут следующим образом: «… в приложении 1…».