Главные оси и главные моменты инерции

Оси, относительно которых центробежный момент инерции равен нулю, называются главными, а моменты инерции относительно этих осей называются главными моментами инерции.

Перепишем формулу (2.18) с учетом известных тригонометрических соотношений:

;

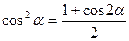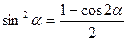
в таком виде

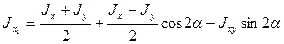(2.21)

С целью определения положения главных центральных осей, продифференцируем равенство (2.21) по углу α один раз получим

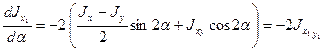(в)

При некотором значении угла α=α₀, центробежный момент инерции 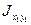может оказаться равным нулю. Следовательно, с учетом производной (в), осевой момент 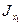инерции примет экстремальное значение. Приравнивая

,

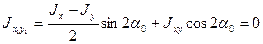получаем формулу для определения положения главных осей инерции в виде:

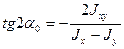(2.22)

В формуле (2.21) вынесем за скобки соs2α₀ и подставим туда значение (2.22) и с учетом известной тригонометрической зависимости 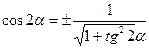получим:

,

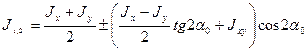или

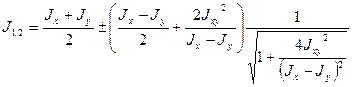
После упрощения окончательно получим формулу для определения значений главных моментов инерции:

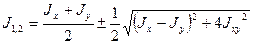(2.23)

Формула (20.1) применяется для определения моментов инерции относительно главных осей. Формула (2.22) не дает прямого ответа на вопрос о том: относительно какой оси момент инерции будет максимальный или минимальный. По аналогии с теорией по исследованию плоского напряженного состояния приведем более удобные формулы для определения положения главных осей инерции:

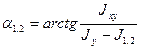(2.24)

Здесь α₁ и α₂ определяют положение осей, относительно которых моменты инерции соответственно равны J₁ и J₂. При этом следует иметь в виду, что сумма модулей углов α₀₁ и α₀₂ должна равняться π/2:

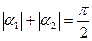(2.24)

Условие (2.24) является условием ортогональности главных осей инерции плоского сечения.

Следует отметить, что при пользовании формулами (2.22) и (2.24) для определения положения главных осей инерции должна соблюдаться такая закономерность:

Главная ось, относительно которой момент инерции максимален, составляет наименьший угол с той исходной осью, относительно которой момент инерции больше.

Пример 2.2.

Определить геометрические характеристики плоских сечений бруса относительно главных центральных осей:

Решение

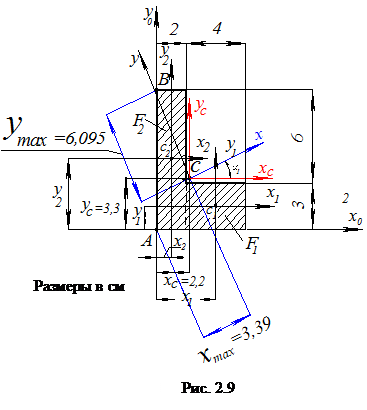
Предложенное сечение является несимметричным. Поэтому положение центральных осей будет определяться двумя координатами, главные центральные оси будут развернуты относительно центральных осей на определенный угол. Отсюда вытекает такой алгоритм решения задачи по определению основных геометрических характеристик.

1. Разбиваем сечение на два прямоугольника с такими площадями и моментами инерции относительно собственных центральных осей:

F₁=12 cм², F₂=18 cм²;

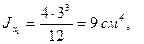
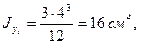
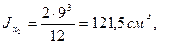
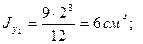
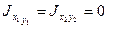
2. Задаемся системой вспомогательных осей х₀у₀ с началом в точке А. Координаты центров тяжести прямоугольников в этой системе осей такие:

х₁=4 см; х₂=1 см; у₁=1,5 см; у₂=4,5 см.

3. Определяем координаты центра тяжести сечения по формулам (2.4):

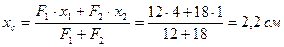
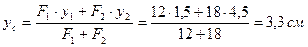
Наносим центральные оси (на рис 2.9 красным цветом).

4. Вычисляем осевые и центробежный моменты инерции относительно центральных осей х_с и у_с по формулам (2.13) применительно к составному сечению:

;

.

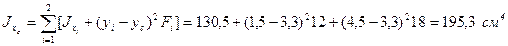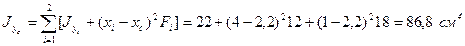
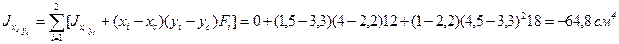5. Находим главные моменты инерции по формуле (2.23)

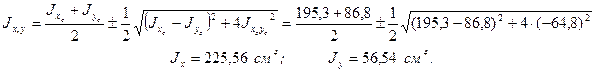
6. Определяем положение главных центральных осей инерции х и у по формуле (2.24):

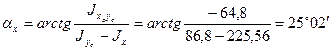
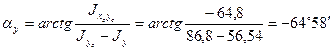
Главные центральные оси показаны на (рис. 2.9) синим цветом.

7. Проверим проведенные вычисления. Для этого проведем следующие вычисления:

- сумма осевых моментов инерции относительно главных центральных и центральных осей должна быть одинаковой:

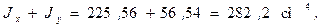
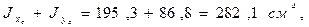
- сумма модулей углов α_х и α_у,, определяющих положение главных центральных осей:

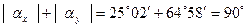
Кроме того, выполняется положение о том, что главная центральная ось х, относительно которой момент инерции J_x имеет максимальное значение, составляет меньший угол с той центральной осью, относительно которой момент инерции больше, т.е. с осью х_с.

- центробежный момент инерции относительно главных осей должен быть равен нулю:

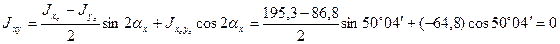
Условия контроля вычислений выполняются.

8. Вычисляем радиусы инерции относительно главных центральных осей по формулам (2.10)

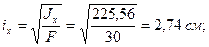
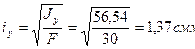
9. Для вычисления осевых моментов сопротивления относительно главных центральных осей отыскиваем наиболее удаленные точки от главных осей инерции. Так точка А наиболее удалена от главной оси у, что определяется координатой x_max, а точка B наиболее удалена от главной оси x, что определяется координатой y_max. Эти координаты найдем по формулам (а) (п. 2.5):

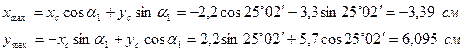
Теперь находим осевые моменты сопротивления по формулам (2.11)

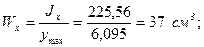
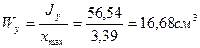
Таким образом, все геометрические характеристики найдены.