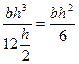Определение нормальных напряжений при чистом изгибе балки
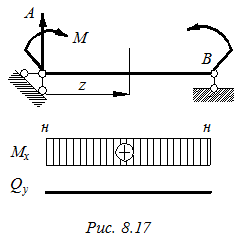 Рассмотрим балку, работающую в условиях чистого изгиба (8.17). В этом случае в поперечных сечениях действуют только изгибающие моменты Мх, а поперечные силы Qy равны нулю (рис. 8.17). Изгибающий момент является равнодействующей внутренних усилий.
Рассмотрим балку, работающую в условиях чистого изгиба (8.17). В этом случае в поперечных сечениях действуют только изгибающие моменты Мх, а поперечные силы Qy равны нулю (рис. 8.17). Изгибающий момент является равнодействующей внутренних усилий.
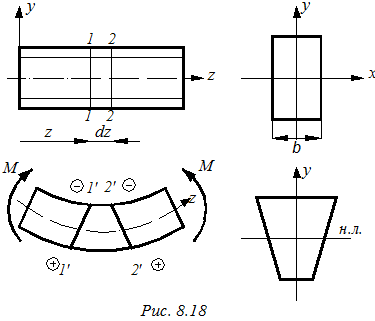
Поперечное сечение балки имеет ось симметрии y. Задача определения нормальных напряжений является статически неопределимой, так как не известен закон распределения нормальных напряжений по высоте сечения балки. Следовательно, помимо условий равновесия, необходимо рассмотреть дополнительные условия деформации балки. Рассмотрим результаты экспериментальных наблюдений. До нагружения на боковую поверхность балки нанесем сетку горизонтальных и вертикальных линий (рис. 8.18). На рис. 8.18 для простоты показаны только по две линии. Будем полагать, что балка в продольном направлении состоит из отдельных волокон, а поперечном - состоит из плоских сечений. Это, так называемая, модель изгиба балки.
После приложения нагрузки балка деформируется, продольные волокна искривляются: нижние волокна удлиняются, верхние - укорачиваются. Сечения 1:1 и 2:2 поворачиваются по отношению к первоначальному положению, оставаясь при этом плоскими. Между зоной растяжения и сжатия существуют волокна, которые в процессе деформации не меняют своей длины, а только искривляются. Эти волокна образуют нейтральный слой.
Нейтральная линия - пересечение нейтрального слоя с плоскостью поперечного сечения. Нейтральная линия делит поперечное сечение балки на две области, напряжения в которых имеют противоположный знак. Следовательно, на самой нейтральной линии напряжения равны нулю.
 |
Вследствие наличия поперечных деформаций, что легко можно установить с помощью тензометров, верхний поперечный размер балки увеличивается, нижний – сужается.
Анализируя данные эксперимента, можно сформулировать следующие гипотезы чистого изгиба балки:
· Гипотеза плоских сечений. Сечения, плоские до загружения балки, остаются плоскими и после загружения, поворачиваясь вокруг некоторой линии.
· Волокна балки при чистом изгибе не давят друг на друга, а находятся в состоянии простого растяжения.
 Деформация балки изменяется по высоте сечения, а по ширине остается постоянной. Следствием этого является сохранение оси симметрии при загружении. После загружения поперечные сечения имеют вид равнобокой трапеции.
Деформация балки изменяется по высоте сечения, а по ширине остается постоянной. Следствием этого является сохранение оси симметрии при загружении. После загружения поперечные сечения имеют вид равнобокой трапеции.
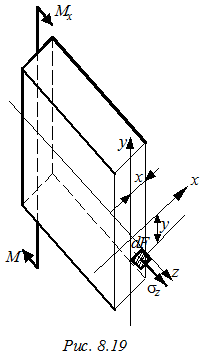
Для составления уравнения статики поперечным сечением отсечем левую часть балки и рассмотрим ее в равновесии под действием внешних и внутренних усилий (рис. 8.19).
z – продольная ось балки,
y – ось симметрии, совпадающая с плоскостью загружения,
х – нейтральная ось, положение которой пока не известно.
В зоне растянутых волокон выделяем бесконечно малый элемент dF, на который действуют растягивающие напряжения σz. Система сил, приложенных к элементу, объемная. Из шести уравнений статики можно записать только три:
ΣFz = 0 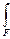 σz.dF = 0 (8.4)
σz.dF = 0 (8.4)
Σmy = 0 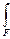 σz.dFx = 0 (8.5)
σz.dFx = 0 (8.5)
Σmx = 0 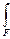 σz.dFy = 0 (8.6)
σz.dFy = 0 (8.6)
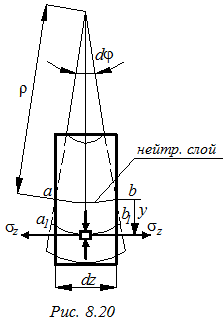 Рассмотрим деформацию волокна длиной dz (рис. 8.20), взятого на расстоянии y от нейтральной оси.
Рассмотрим деформацию волокна длиной dz (рис. 8.20), взятого на расстоянии y от нейтральной оси.
dz = ρ dφ
ρ - радиус кривизны нейтрального слоя,
dφ - угол, образованный двумя смежными сечениями после деформации.
Длина волокна аb после загружения - а1b1.
а1b1 = (ρ + y)dφ
Относительная деформация волокна
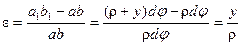
Согласно второй гипотезе бесконечно малый элемент, выделенный в пределах рассматриваемого волокна, будет испытывать чистое растяжение. Поэтому на основании закона Гука можно записать
σz.= εE = 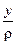 E (8.7)
E (8.7)
Подставляя полученное выражение (8.7) в уравнение (8.6) найдем
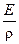
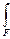 y ydF = Mx (8.6)
y ydF = Mx (8.6)
Учитывая, что 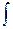 y2dF = Ix, получим
y2dF = Ix, получим 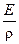 Ix = Mx или
Ix = Mx или 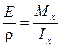
После подстановки в уравнение (8.7) имеем
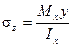 (8.8)
(8.8)
Кривизна балки определяется по формуле
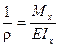 (8.9)
(8.9)
При чистом изгибе Mx = const, следовательно 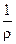 = const
= const
Отсюда следует, что балка при чистом изгибе изгибается по дуге окружности.
Произведение EIx - жесткость балки при изгибе.
Полученное выражение (8.8) подставим в формулу (8.4)
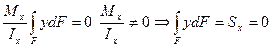
Отсюда следует, что нейтральная линия совпадает с центром тяжести сечения и является центральной осью.
Теперь полученное выражение (8.8) подставим в формулу (8.5)
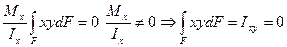
Это возможно в том случае, когда оси х и у являются главными осями инерции.
Следовательно, в формуле (8.8) оси х и у являются главными центральными.
Методами «Теории упругости» доказано, что полученная формула (8.8) может быть применима и при поперечном изгибе, когда в сечениях балки действуют не только изгибающие моменты, но и поперечные силы. Это возможно в том случае, когда длина балки l больше ее высоты h в пять и более раз. Из формулы (8.8) следует, что нормальные напряжения по высоте сечения меняются по линейному закону. При этом максимальные напряжения по высоте сечения возникают в зоне верхних и нижних волокон, которые наиболее удалены от нейтральной оси.
σ = 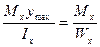 (8.10)
(8.10)
Здесь обозначено: 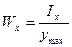 момент сопротивления площади поперечного сечения относительно нейтральной оси х или просто осевой момент сопротивления.
момент сопротивления площади поперечного сечения относительно нейтральной оси х или просто осевой момент сопротивления.
Для прямоугольного сечения
Wx =