Вероятностные характеристики обнаружения
Задача любого ОЭП в режиме обнаружения – выдача решения о наличии или отсутствии в поле зрения прибора объекта пеленгации. Информация, которая используется для принятия решения, должна быть извлечена из поступающего на вход прибора воздействия в виде потока энергии. Это воздействие, которое обозначим через y(t), является функцией времени и представляет собой некоторую комбинацию полезного сигнала s(t) и фоновой помехи n(t).
В общем виде характер взаимосвязи полезного сигнала и помехи может быть выражен некоторым оператором:
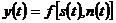 . (1)
. (1)
Если оператор вырождается в произведение, т.е.
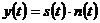 , (2)
, (2)
то такая помеха называется мультипликативной. Природа этой помехи часто связана со случайным изменением параметров канала связи, например, коэффициента пропускания атмосферы. Если же оператор может быть представлен в виде суммы, т.е.
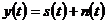 , (3)
, (3)
то такая помеха называется аддитивной. Этот случай легче поддается анализу.
Так как момент появления объекта в поле зрения прибора заранее предсказать невозможно, а помеха имеет случайный характер, то в каждом конкретном случае y(t) является одной из возможных реализаций случайного процесса. Такую реализацию обозначим буквой Y.
Реализация Y может содержать в себе полезный сигнал (если цель находится в поле зрения прибора), а может и не содержать. Обозначим вероятность присутствия полезного сигнала в реализации через P(s/y), а вероятность его отсутствия - через P(0/y). Эти вероятности называются апостериорными условными вероятностями наличия и отсутствия полезного сигнала в реализации. Апостериорными они называются потому, что их можно определить только после опыта, т.е. после получения и анализа реализации. Условными их называют потому, что они соответствуют условию получения данной конкретной реализации. Если вид реализации изменится, то изменятся и получаемые значения P(s/y) и P(0/y).
Величины P(s) и P(0) определяют априорные вероятности наличия и отсутствия полезного сигнала. В задаче обнаружения оба события являются противоположными и справедливы следующие равенства:
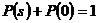 ; (4)
; (4)
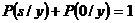 (5)
(5)
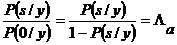 . (6)
. (6)
Величина Λа называется абсолютным отношением правдоподобия, оно полностью определяет вероятность наличия (отсутствия) сигнала в реализации.
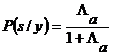 ; (7)
; (7)
Если бы, например, анализ реализации показал, что Λа>1, то P(s/y)>1/2. Следовательно, 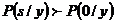 , и более обоснованным было бы принятие решения «Да» (объект находится в поле зрения прибора), чем альтернативное «Нет».
, и более обоснованным было бы принятие решения «Да» (объект находится в поле зрения прибора), чем альтернативное «Нет».
К сожалению, для определения Λа необходимо извлечь из анализа полученной реализации величину отношения
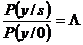 , (8)
, (8)
но и знать априори P(s) или P(0), что на практике чаще всего не представляется возможным.
Величина Λ называется отношением правдоподобия, при определенных условиях может быть найдена на основании анализа полученной реализации.
Принятие любого решения всегда может сопровождаться ошибками. Работа прибора в неопределенной ситуации (объект может находиться в поле зрения, а может и не находиться) при воздействии случайных помех также сопровождается ошибками, которые имеют вероятностный характер и, в той или иной степени, характеризуют качество прибора как системы обнаружения.
Возможны ошибки двух типов. Первая, называемая ошибкой ложной тревоги, возникает, когда при отсутствии объекта в поле зрения прибор выдает решение «Да». Вторая, соответствует случаю, когда при наличии объекта в поле зрения прибор выдает решение «Нет». Эта ошибка называется ошибкой пропуска объекта (сигнала).
Обозначим событие, заключающееся в выдаче прибором решения «Да», через γs, а событие, заключающееся в выдаче решения «Нет», через γ0. Тогда вероятности появления ошибок первого и второго типов можно обозначить как Р(γs/0) и Р(γ0/s).
Вероятность Рл.т.= Р(γs/0), т.е. вероятность принятия решения γs («Да») при условии отсутствия объекта обнаружения в поле зрения прибора, называется условной вероятностью ложной тревоги.
Вероятность Рпр.= Р(γ0/s), т.е. вероятность принятия решения γ0 («Нет») при условии наличия объекта в поле зрения, называется условной вероятностью пропуска объекта.
Р(γ0/s)+ Р(γs/s)=1
Р(γ0/0)+ Р(γs/0)=1,
отсюда можно получить:
Робн= Р(γs/s)=1 - Р(γ0/s)=1 – Рпр ;
Рп.н= Р(γ0/0)= 1 - Р(γs/0)=1 – Рл.т. .
Величина Робн называется условной вероятностью правильного обнаружения, а величина Рп.н – условной вероятностью правильного необнаружения.
Чем меньше Рпр и Рл.т.(т.е. чем большие значения Робн и Рп.н) реализует система обнаружения, тем выше ее качество.
Приемник должен дать ответ: есть или нет объект в поле зрения прибора:
- правильное обнаружение;
- правильное необнаружение;
- ложная тревога, когда полезного сигнала нет, но уровень помех превышает некоторый необходимый для правильного срабатывания ОЭС уровень y0 ;
- пропуск сигнала, когда объект есть, а система его не фиксирует.
Обозначим через Ps(y) и Pn(y) – условные априорные вероятности смеси сигнала и помехи.
Рy – плотность вероятности смеси сигнала и помехи;
Рn - плотность вероятности помехи, тогда условная вероятность правильного обнаружения:
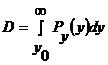 ,
,
а пропуска
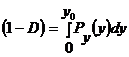 .
.
Если сигнал отсутствует, если уровень порога неправильно выбран, условная вероятность ложной тревоги:
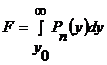 ,
,
а условная вероятность правильного необнаружения:
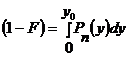 .
.
Чем выше y0, тем выше вероятность правильного обнаружения и ниже вероятность ложной тревоги.
 |
