Затененная поверхность с подсветкой

MATLAB имеет команды, которые дают возможность управлять подсветкой построенной поверхности. Это реализуется командой:surfl(X, Y, Z, s)

Команда surfl(X, Y, Z, s) выводит на экран затененную поверхность с подсветкой для значений массива Z, определенных на множестве значений массивов X и Y. Направление на источник света может быть задано с помощью вектора s = [Sx, Sy, Sz] в декартовых координатах или вектора s = [az, elev] в сферических координатах. По умолчанию азимут az = -37.5°, возвышение elev = 30°. Подсветка учитывает модели рассеяния, отражения и зеркального эффекта освещения поверхности.

Команда surfl(X,Y, Z, s, k) позволяет управлять параметрами рассеяния, отражения и зеркального эффекта, используя вектор

k = [ka, kd, ks, spread], который учитывает эффекты отраженного света ka, диффузного отражения kd, зеркального отражения ks и зеркального распространения spread. По умолчанию вектор k имеет значения [0.55, 0.6, 0.4 ,10].

Команда surfl(X, Y, Z) использует значения параметров по умолчанию.

Команды surfl(Z, ...) строят графики, не учитывая истинных значений массивов X и Y.

Из-за того что алгоритм surfl вычисляет нормали к поверхности, необходимо, чтобы входные матрицы имели размер по крайней мере 3 х 3.

Пример 5.14.Построить поверхность стандартной функции peaks на квадрате [-3,3]*[-3,3], используя подсветку.

>> [X,Y]=meshgrid(-3:1,8:3);
>> Z = peaks(X, Y);
>> surfl(X, Y, Z)
>> shading interp
>> colormap(gray)

Рис.12. Поверхность с параметрами

подсветки по умолчанию

Трехмерная поверхность

Если не требуется при построении поверхности функции z=f(x,y) отображать рёбра, соединяющие значения функции в узлах, а, обозначив её параллельными линиями, соответствующими сечением, нужно использовать команды:

waterfall(X, Y, Z, C)

Команда waterfall(X, Y, Z, C) строит поверхность для значений массива Z, определенных на множестве значений массивов X и Y. Она аналогична команде mesh, но не прорисовывает ребер сетки.

Команда waterfall(x, y, Z, C) выполняет ту же функцию, но вместо двумерных массивов X, Y использует их одномерные проекции, так что если length(x) = n, а length(y) = m, то [m, n] = size(Z).

Команда waterfall(Z, C) использует сетку, которая определяется одномерными массивами x = 1 : n и y = 1 : m.

Команды waterfall(X, Y, Z), mesh(x, y, Z), mesh(Z) используют в качестве массива цвета C = Z, то есть цвет в этом случае пропорционален высоте поверхности. Функция h = waterfall(...) возвращает вектор дескрипторов h для графических объектов patch.

Пример 5.15.

Построить трехмерную поверхность функции 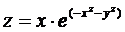в квадрате [-2,2] x [-2,2].

>> [X,Y]=meshgrid(-2:0.1:2]);
>> Z = X .*exp(- X .^2 - Y .^2);
>> waterfall(X, Y, Z)

Рис.13. Поверхность функции из примера 5.15

Поле градиентов функции

Пусть функция z=f(x,y) задана в прямоугольной области [a,b] x [c,d]. Рассмотрим разбиение области на узлы . Если в каждом узле вычислить градиент , получим для каждой пары (i,j) вектор . Тогда градиентное поле можно построить, используя команду:

quiver(X, Y, DX,DY)

Команда quiver(X, Y, DX, DY) формирует и выводит на экран поле градиентов функции в виде стрелок для каждой пары элементов массивов X и Y, а пары элементов DX и DY используются для указания направления и размера стрелки.

Команда quiver(x, y, DX, DY), где x и y - одномерные массивы размеров length(x) = n и length(y) = m, где [m, n] = size(DX) = size(DY), формирует и выводит на экран поле градиентов для каждой точки; стрелки задаются четверками {x(j), y(i), DX(i, j), DY(i, j)}. Обратите внимание, что x соответствует столбцам DX и DY, а y - строкам.

Команда quiver(DX, DY) использует массивы x =1:n и y =1:m.

Команды quiver(x, y, dx, dy, s), quiver(dx, dy, s) используют скаляр s как коэффициент масштаба стрелки, например s = 2 вдвое увеличивает, а s = 0.5 вдвое уменьшает размер стрелки.

Команда в форме quiver(... ‘<тип_линии>’) позволяет задать тип и цвет линии по аналогии с функцией PLOT.

Пример 5.16.Построить поле направлений и линии уровня для функции 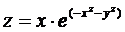в области ,

>> [x, y] = meshgrid(-2 : .2 : 2); % сетка
>> z = x.*exp(-x.^2 - y.^2); % значения функции
>> [dx, dy] = gradient(z, .2, .2); % градиент в узлах
>> contour(x, y, z), hold on % линии уровня
>> quiver(x, y, dx, dy) % поле градиентов

Рис.14. Результат примера 5.16

Пример 5.17.Рассмотрим тело, брошенное под заданным углом к горизонту. Требуется построить векторы скорости в узлах траектории. Координаты тела определяются по следующим формулам:

x=t/2, y=0.8t(1-t/2).

>> t = 0:0.2:2; x = 0.5*t; y = 0.8*t.*(1 - 0.5*t); % Траектория

>> ux(1:length(x)) = 0.5; uy = 0.8*(1 - t);

% Вектор скорости в узлах

>> quiver(x, y, ux, uy) % Векторное поле

Рис.15. Векторы скоростей в узлах (пример 5.17).