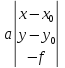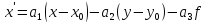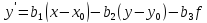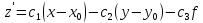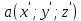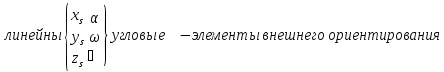Теорема Шаля. Масштаб перспективы.
Теорема Шаля классифицирует все изометрические преобразования (движения) плоскости.
Всякое сохраняющее ориентацию движение плоскости представляет собой либо поворот (в частности, центральную симметрию), либо параллельный перенос. Всякое меняющее ориентацию движение плоскости является осевой или скользящей симметрией.
Известно, что бесконечно продолженная прямая в перспективе ограничена предельной точкой (см. рис. 17, 18). Отсюда плоскость в перспективе ограничена предельной прямой, которая образована совокупностью предельных точек прямых, лежащих в этой плоскости. Так получена линия горизонта как предельная прямая предметной плоскости. На рисунке 57, а, б рассмотрен случай получения перспективы не всей заданной плоскости, а только ее части, поэтому она ограничена линией обрыва. Рассмотрим на проецирующем аппарате (рис. 58, а) получение изображения на картине всей плоскости. Для этого строят ее предельную прямую. С этой целью из точки зрения S направляют пучок лучей в бесконечно удаленные точки прямых заданной плоскости.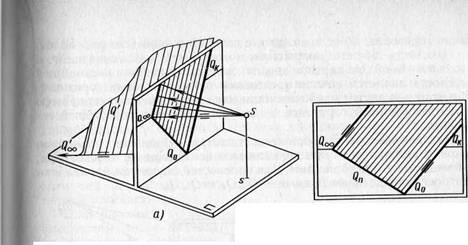 
Рис 57 Каждый луч пройдет параллельно плоскости Q' и пересечет картину в одной из точек искомой предельной прямой. Следовательно, совокупность направленных лучей зрения образует лучевую плоскость, расположенную параллельно заданной плоскости Q'. Линия пересечения лучевой плоскости с картиной представит предельную прямую данной плоскости Q'. Из выполненных построений вытекают два положения: 1) предельная прямая плоскости параллельна ее картинному следу, так как обе прямые получены в результате пересечения двух параллельных плоскостей (лучевой и заданной) третьей плоскостью - картиной; 2) предельная прямая проходит через предельную точку предметного следа заданной плоскости, так как предельная точка - это перспектива одной из бесконечно удаленных точек прямой заданной плоскости. Отсюда следует, что предельную прямую плоскости, заданной следами, проводят через предельную точку предметного следа параллельно картинному (рис. 58, б). Итак, бесконечно продолженная плоскость общего положения в перспективе имеет предел и ограничена предельной прямой, которая проходит через предельную точку ее предметного следа параллельно картинному следу. (Закон предельной прямой плоскости общего положения.)
21. Системы координат принятые в фотограмметрии.
Основная задача фотограмметрии – определить координаты точек объекта по их изображениям на снимках. Для этого необходимо выполнить измерения на снимках и установить связь между системой координат в которой выполнялись измерения и системой координат используемой на местности.
Системы координат:
1. СК снимка
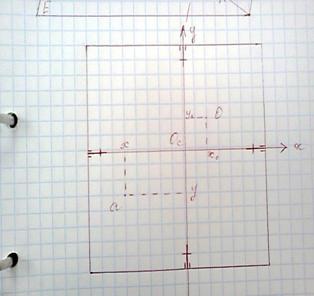
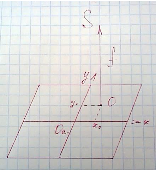
Система координат снимков задается координатными метками.
Oс – начало системы координат
Ocxy – плоскость снимка
a(x, y) - Координаты точки a в системе координат снимка
xo, уо – в системе координат снимка
f, yo, xo элементы внутреннего ориентирования снимка. Они определяют положение точки картографирования С относительно системы координат снимка и позволяют восстановить связку лучей существовавшую в момент съемки. Определяются заводом изготовителем и записываются в паспорт
2. Пространственная СК съемочной камеры
S, x,y,я - Пространственная система координат съемочной камеры. Начало которой находится в точке фотографирования S. Оси x, y направлены параллельно осям x, y снимка, а ось z направлена вдоль главного луча (перпендикулярно плоскости снимка)
3. Внешняя система координат – система в которой определяются координаты точек местности. Она мб задана условно, но чаще всего используется в геодезической СК.
Ог, x(г), y(г), z(г) – Внешняя СК (геодезическая), которую фотограмметристы называют геодезической
4. Фотограмметрическая система координат
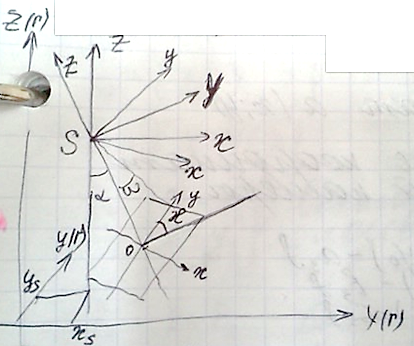
SXYZ – фотограмметрическая СК
Начало в точке S
α –– угол между осью Z и проекцией главного луча на плоскость xZ
ω – поперечный угол – угол между главным лучом и плоскостью xZ
ᴂ - угол разворота снимка – угол в плоскости снимка между осью y и следом плоскости проходящей через главный луч SО и ось Y
Положение системы Sxyz относительно системы SXYZ описывается матрицей поворота А;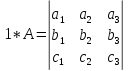 
, гдеabc – направляющие косинусы.
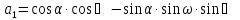
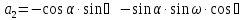
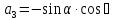
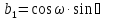
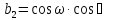
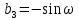
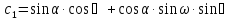
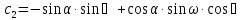
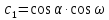
В системе координат снимка a (x,y)
