Особенности измерения цифровых снимков

Средства измерений

Измерение цифровых снимков выполняется на экране монитора. Оно может быть как монокулярным, если отображается один снимок (растр) и стереоскопическим, когда на экране присутствуют растры, составляющие стереопару, а технология требует именно такого варианта измерений.

В качестве измерительной марки используется курсор (или два курсора). Его (их) форма, размер и цвет зависят от того, какой технологический процесс выполняется, а также могут устанавливаться и пользователем. Перемещение курсора (курсоров) осуществляется мышкой, соответствующими кнопками клавиатуры, а на фотограмметрической станции ЦФС, кроме того, ножным и ручными штурвалами. Методы стереонаблюдения: оптический, миганий и анаглифический.

Первый используется на ЦФС, для чего перед экраном дисплея устанавливается стереоскоп. В методе миганий используются затворные (жидкокристаллические) очки, в которых попеременно открывается изображение, то для левого, то для правого глаза, Синхронно с работой очков чередуются изображения снимков на экране монитора. При этом возможен интерлейсный режим при котором кадр делится на два полукадра, первый из которых содержится в четных строчках, а второй – в нечетных (при этом происходит снижение разрешения и возникают некоторые неудобства при работе с меню). Возможно и покадровое стерео (режим page-flipping). Оно обеспечивает более качественный стереоэффект, в связи с использованием полных кадров. Для того, чтобы оператор не уставал, нужна высокая частота вертикальной развертки. Как отмечалось выше, она должна быть не менее 120 Гц.

При анаглифическом методе на экране отображаются в разных цветах два наложенных друг на друга растра (например, красный и синий), а оператор должен использовать анаглифические очки. Как правило, есть возможность варьировать цветами растров и подобрать наилучший вариант (исходя из цветов стекол очков и пристрастий оператора).

Обычно в программных продуктах реализовано несколько вариантов стереонаблюдений, и можно переходить от одного к другому, но, по отзывам производственников, анаглифический метод измерений наименее точен, и его следует использовать как вспомогательный вариант. Кроме того, всеми разработчиками предусматривается переключение от прямого стереоэффекта к обратному, что очень полезно при работе со снимками залесенных и застроенных территорий. Возможна и коррекция самих растровых изображений (изменение плотности, контрастности и т.д.).

Большим достоинство измерения цифровых снимков является то, что после позиционирования одного из курсоров, второй можно навести на соответственную точку автоматически, используя механизм корреляции. Он же позволяет автоматически сгущать число соответственных точек или набирать их в виде сетки квадратов, что важно для взаимного ориентирования снимков и построения цифровой модели рельефа. Но результат работы коррелятора нужно все время контролировать, особенно на однотонных участках снимков.

5.3.2 Принципы измерений (Михайлов)

Цифровое изображение хранится в памяти компьютера, в общем случае, в виде прямоугольной матрицы, элементы которой несут информацию об оптических плотностях или цвете элементарных участков изображения, а номера i строки и j столбца элемента определяют его положение в матрице. Нумерация строк и столбцов матрицы цифрового изображения начинается с нуля.

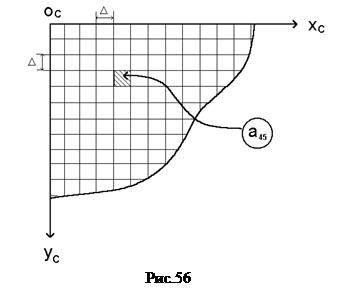
Координаты центров пикселов в левой прямоугольной системе координат цифрового изображения оC xC УC .(рис. 56), началом которой является левый верхний угол цифрового изображения, определяются в, так называемых, пиксельных координатах (единицей измерения в этом случае является пиксел) по формулам:

xp =j + 0.5, yp =i + 0.5

(125)

Для измерения координат точек цифрового изображения его визуализируют на экране дисплея. Если пиксел изображения на экране дисплея соответствует пикселу исходного цифрового изображения, то с помощью “мыши” или клавиатуры компьютера можно навести измерительную марку, формируемую в виде цифрового изображения на экране дисплея, на точку изображения с точностью до одного пиксела.

Для получения подпиксельной (субпиксельной) точности можно увеличить матрицу изображения на экране монитора относительно исходного цифрового изображения. В этом случае каждый пиксел исходного изображения будет изображаться матрицей n×n пикселов, численное значение всех элементов a'ij которой будут равны численному значению элемента матрицы исходного изображения.

Пиксельные координаты точек увеличенного изображения можно измерить с точностью до 1/n пиксела исходного изображения (рис.57).

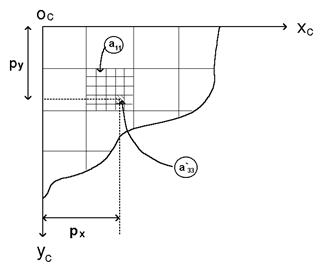Рис. 57

Пиксельные координаты (в пикселах исходного изображения) элемента a'ij увеличенного изображения определяют по формулам:

xp =j +(j΄ + 0.5)/n, yp =i + (i΄ + 0.5)/n

(126)

Причем i, j - номера строки и столбца элемента матрицы исходного изображения, в котором находится элемент a'ij увеличенного изображения, а i΄,j΄ - номера строки и столбца элемента a`ij подматрицы n×n; n – коэффициент увеличения изображения.

Например, для элемента a’33 (рис.57) пиксельные координаты:

x_p = 1 +(3 + 0.5)/5 =1.7 , y_p = 1 +(3 + 0.5)/5 =1.7

Значения координат центров пикселов цифрового изображения в метрической системе можно определить по значениям их пиксельных координат, используя соотношение:

xc = Δ·xp и yc = Δ·yp,

(127)

если известны физические размеры Δ стороны пиксела изображения (предполагается, что пиксел имеет форму квадрата). Например, координаты центра пиксела, соответствующего элементу a’33 (рис. 56) при величине Δ=20 мкм будут равны х_c = 34 мкм и y_c = 34 мкм.

В некоторых цифровых системах начало системы координат цифрового изображения оC хC уC выбирают в центре пиксела, расположенного в верхнем левом углу цифрового изображения. В этом случае значения пиксельных координат вычисляют по формулам:

xp =j и yp =i

(128)

при измерениях с точностью до пиксела и по формулам:

xp =j – 0.5+(j΄ + 0.5)/n, yp =i – 0.5+ (i΄ + 0.5)/n

(129)

при измерениях с субпиксельной точностью.

Метод измерения цифрового изображения с субпиксельной точностью требует его увеличения на экране дисплея компьютера. Однако, даже при увеличении только в два раза, исходный аналоговый снимок может оказаться увеличенным на экране дисплея в 40 раз. Это приводит к значительному ухудшению изобразительных свойств наблюдаемого изображения и, как следствие, к снижению точности наведения измерительной марки на измеряемые объекты на изображении.

Для его реализации без увеличения исходного изображения, разработан метод, в котором цифровое изображение снимка может смещаться относительно неподвижной измерительной марки с шагом в n – раз меньшим размера пиксела.

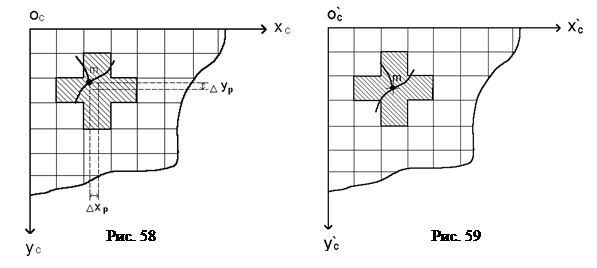
Принцип такого метода измерения координат точек иллюстрируется на рис. 58 и 59.

На рис.58 представлен фрагмент исходного цифрового изображения с измерительной маркой и точкой m, координаты которой необходимо измерить. Из рисунка следует, что центр изображения марки не совпадает с изображением точки m, причем разности значений их пиксельных координат составляют величины Dx_p и Dy_p. Для совмещения центра изображения измерительной марки с точкой m можно создать фрагмент цифрового изображения снимка, в котором координаты начала системы координат o_c^΄ x_c^΄ y_c будут иметь значения 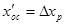, а .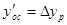

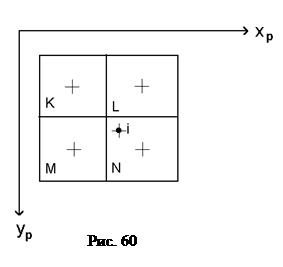
Создается такой фрагмент следующим образом. По координатам центра каждого пиксела фрагмента изображения x΄_pi, y΄_pi определяют значения координат его проекции x_pi, y_pi в системе координат ох_cу_c исходного изображения. Для этого используют формулы: x_pi= x΄_pi+ Δx_pi, y_pi= y΄_pi+ Δy_pi. Затем по значениям координат x_pi, y_pi находят ближайшие к изображению точки i, соответствующей центру пиксела создаваемого фрагмента цифрового изображения, четыре пиксела исходного цифрового изображения, например, M, K, L, N (рис. 60).

Далее методом билинейного интерполирования определяют значения оптической плотности i-го пиксела создаваемого фрагмента изображения. При этом:

Di = D1 + (D2 – D1)DXp,

(130)

причем

D1 = DK + (DM – DK)DYP, D2 = DL + (DN – DL)DYP,

Таким же образом формируются все элементы создаваемого фрагмента цифрового изображения.

На экране дисплея, на визуализированном фрагменте созданного цифрового изображения центр измерительной марки будет совмещен с изображением точки m. Ее пиксельные координаты в системе координат исходного изображения определяются по формулам 129.

Необходимо отметить, что создание фрагмента цифрового изображения требует значительных вычислительных процедур. Поэтому для достижения эффекта перемещения изображения на экране дисплея относительно марки в “реальном масштабе” времени фрагмент изображения не должен иметь большие размеры.

В случае если для измерений используются цветные цифровые изображения при формировании элементов создаваемого изображения методом билинейного трансформирования по формулам 130. определяются интенсивности красного (R), зеленого (G) и синего (В) компонентов цветного изображения.