В магазине имеется в продаже 20 пар обуви, из которых 7 пар 42 размера. Найти вероятность того, что из 8 покупателей 3 выберут обувь 42 размера.
Решение:P(A)=m/n
C37 =7!/ (7-3)!3! = (4!*5*6*7)/(4!*1*2*3)=35
C513=13!/(13-5)!5!=(8!*9*10*11*12*13)/(8!*1*2*3*4*5) = 1287
C820 = 20! /(20-8)!8! = (12!*13*14*15*16*17*18*19*20)/(12!*1*2*3*4*5*6*7*8) =126000
P(A)= C37 * C513 / C820 =35*1287 /126000 = 0,36
34. В мешке смешаны нити трех цветов: 30% белых, 50% красных, остальные зеленые. Определить вероятность того, что при последовательном вытягивании наугад трех нитей окажется, что все они одного цвета.
35. В урне «а» белых и «Ь» черных шаров. Из урны вынули один шар и, не глядя, отложили в сторону. После этого из урны взяли еще один шар. Он оказался белым. Найти вероятность того, что первый шар, отложенный в сторону - тоже белый.
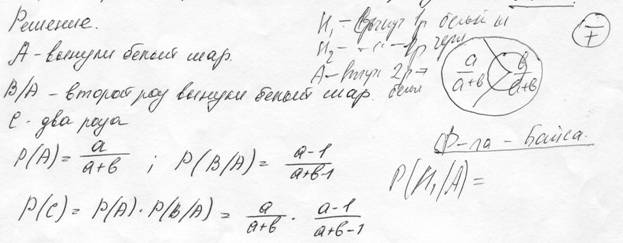
36. У рыбака имеется 2 места ловли рыбы, которые он посещает с одинаковой вероятностью. Если он закидывает удочку на первом месте, рыба клюет с вероятностью 0,6, на втором - с вероятностью 0,7. Рыбак, выйдя на ловлю в одно из мест, 2 раза закинул удочку. Найти вероятность того, что рыба клюнет только один раз.

37.На сборку поступило 50 деталей от первого станка, 100 от второго и 150 от третьего. Первый станок дает 2%, второй 1% и третий 2% брака. Найти вероятность того, что взятая наугад деталь окажется не бракованной. Задачу решить используя а)определение вероятности события; б) формулу полной вероятности.
Решение:а) брак 1 ст. = 0,02* 50 = 100; брак 2 ст. = 0,01*100 = 1 деталь;
брак 3 ст = 0,02*150 = 3 детали.
Всего 300 деталей, из них браковано 5 деталей; не бракованных=295д.
P(A) = 295/300 = 59/60 = 0,98
б) 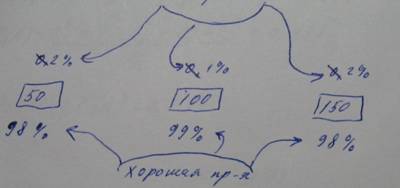
H1 –количество(процентное) деталей сделанных 1-м станком:
H1 : 300 100%
51 H1
H1=16%; P(H1)=0,16; P(H2)=0,33; P(H3)=0,5
H2=33%, H3=50%.
P(A/H1) = 0,98; P(A/H2) = 0,99; P(A/H3) = 0,98
P(A) = 0,98*0,16 + 0,99*0,33+0,98*0,5 = 0,1568+ 0,3267 +0,49 =0,98
Ответ: P(A) = 0,98.
38. Найти вероятность того, что на две определённые карточки в «Спортлото - 5 из 36» будет получено по минимальному выигрышу ( угадано ровно три числа).
Решение:
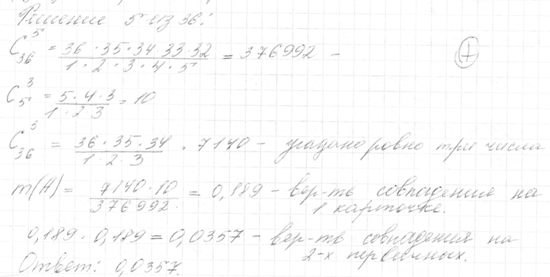
39. Вероятность того, что стрелок попадет, хотя бы один раз при трех выстрелах равна, 0,992. Найти вероятность попадания в цель при одном выстреле, предполагая ее постоянной при каждом выстреле.

40. Пусть 3% всех мужчин и 5% всех женщин дальтоники. Наугад выбиранный человек оказался дальтоником. Какова вероятность, что это мужчина? ( Считать, что количество мужчин и женщин одинаково.)
Решение:

41. В группе из 25 человек 10 учится на «отлично», 8 на «хорошо» и 7 на «удовлетворительно». Найти вероятность того, что из взятых наугад 8 человек 3 человека учатся на «отлично».
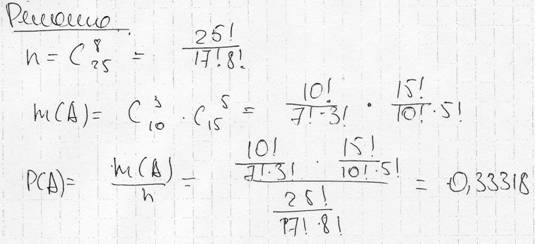
42.Какова вероятность, что наудачу вырванный листок из нового календаря соответствует первому числу месяца? (Год считается не високосным.)
Решение:
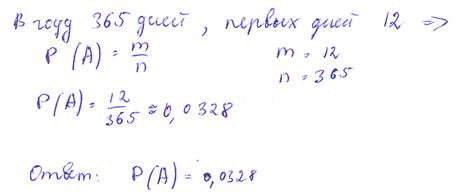
43.В группе спортсменов 10 лыжников, 6 боксеров и 4 бегуна. Вероятность выполнить квалификационную норму для лыжников составляет 0,8, боксеров 0,7, бегунов 0,9. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит квалификационную норму.

На одной полке наудачу расставляют 8 книг. Найти вероятность, что определенные 3 книги окажутся поставленные рядом.
Решение:P(A)=m/n
m= C3(n)8(k)=(k-n+1)
n=8!
C38= 8!/ (8-3)! 3! =(5!*6*7*8) / (5!*1*2*3) = 336/6=56
P(A)= (C38*(8-3+1)/8!=(56*6) / 40320=336/40320 =0,008
45. Монету бросают три раза. Какое из событий более вероятно: событие А - все три раза выпала цифра или событие В - два раза выпала цифра и один раз герб? Подсчитать вероятности этих событий.
Решение:

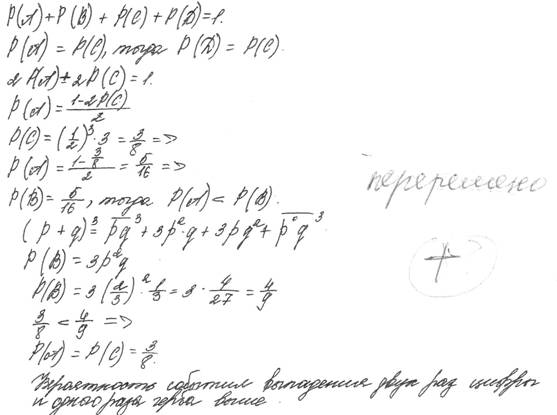
46. К концу дня в магазине осталось 60 арбузов, из которых 50 спелых. Покупатель выбирает два арбуза. Какова вероятность, что оба арбуза спелые?
