Примеры решения типовых задач

Задача 1.

Для получения золя хлорида серебра смешали 15 мл 0,025 н раствора хлорида калия с 85 мл 0,005 н раствора нитрата серебра. Написать формулу мицеллы образовавшегося золя.

Решение.

Рассчитаем количество вещества эквивалентов солей, участвующих в образовании золя: 15·0,025 = 0,375 ммоль-экв. KCl; 58·0,005 = 0,425 ммол-экв. AgNO₃.

По закону эквивалентов в реакцию вступает одинаковое число эквивалентов веществ, следовательно в избытке AgNO₃. В растворе присутствуют ионы Ag⁺, K⁺ и NO₃^–.

В соответствии с правилом Панета-Фаянса потенциалопределяющими являются ионы Ag⁺ , а противоионами NO₃^–. Формула мицеллы:

{[nAgCl]mAg⁺(m-x)NO₃^–}xNO₃^–.

Задача 2.

Электрокинетический потенциал частиц гидрозоля 50 мВ. Приложенное внешнее напряжение 240 В, а расстояние между электродами 40 см. Вычислить электро­фо­ре­ти­чес­кую скорость частиц золя. Вязкость воды 0,001 Па·с, а диэлектрическая проницаемость среды 81.

Решение:

Из уравнения Гельмгольца-Смолуховского электрофоретическая скорость частиц: .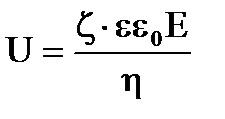

Градиент потенциала: .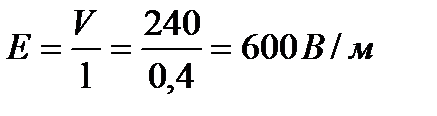

.

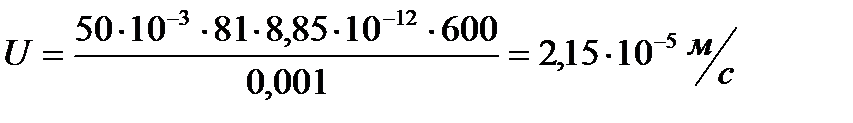Задача 3.

Рассчитайте 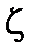― потенциал частиц полистирольного латекса: смещение цветной границы золя (а) при электрофорезе составляет 2,5×10^-2 м за время (t), равное 60 мин. Напряжение, приложенное к электродам, V=115 B. Расстояние между электродами l=0,55 м. Диэлектрическую проницаемость среды принять равной 81. Вязкость среды h=1·10^-3 Па·с.

Решение.

По уравнению Гельмгольца-Смолуховского

.

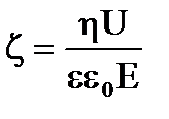Напряженность электрического поля

, .

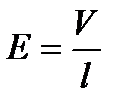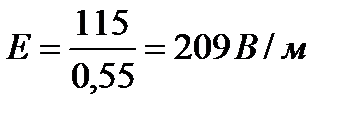Скорость частиц

,

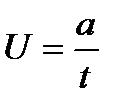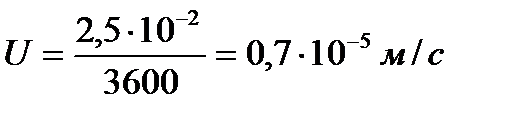
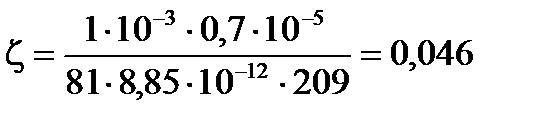В.

Задача 4.

Определить величину объемной скорости электроосмоса n через мембрану водного раствора электролита с c=1,5·10^-3 См·м^-1 при силе тока I=8·10^-5 А, если величина электро­кинетического потенциала x=0,057 В; h=10^-3 Па·с.

Решение.

Из уравнения для электроосмоса:

,

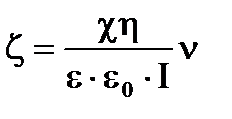откуда объемная скорость электроосмоса:

,

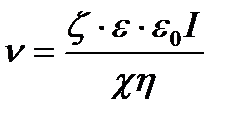Тема 5. Молекулярно-кинетические и оптические свойства
коллоидных систем

Молекулярно-кинетические свойства коллоидных растворов проявляются в броуновском движении, диффузии и осмосе.

Броуновское движение — это непрерывное беспорядочное движение частиц микроскопических и коллоидных размеров, не затухающее во времени. Это движение обусловлено столкновением молекул среды, находящихся в непрерывном тепловом движении, с взвешенными в ней частицами.

Количественной характеристикой броуновского движения считается средний сдвиг частиц 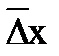за время t. Как показал Эйнштейн, средний квадратичный сдвиг частицы 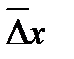может быть вычислен на основании статистических законов из уравнения:

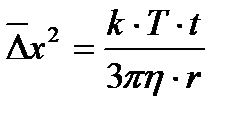, откуда ,

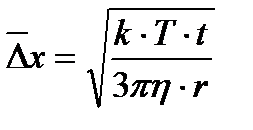где Т − абсолютная температура; t − время наблюдения; h − коэффициент вязкости; r − радиус частицы; k − постоянная Больцмана,

,

где R − универсальная газовая постоянная; N_А − постоянная Авогадро.

Диффузией называется самопроизвольный процесс выравнивания концентрации молекул, ионов или коллоидных частиц под влиянием их теплового движения. Для количественного описания диффузии используется закон Фика:

,

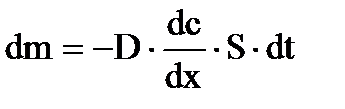где m − количество продиффундировавшего вещества; D − коэффициент диффузии; 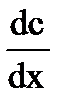− градиент концентрации; S − площадь, через которую происходит диффузия; t − продолжительность диффузии.

Знак минус перед правой частью уравнения означает, что градиент концентрации отрицателен, т.к. концентрация с увеличением х уменьшается.

Для описания диффузии также используется удельный поток диффузии − количество вещества, диффундирующее за единицу времени через сечение единичной площади

.

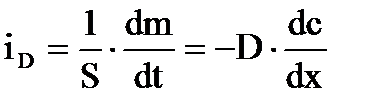Из этого уравнения виден физический смысл коэффициента диффузии D.

Коэффициент диффузии численно равен количеству вещества, диффундирующего через единицу площади в единицу времени при градиенте концентрации, равном единице.

Эйнштейн вывел уравнение, связывающее коэффициент диффузии с абсолютной температурой Т, вязкостью дисперсионной среды η и радиусом частиц дисперсной фазы r:

.

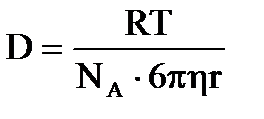Связь между средним квадратичным сдвигом частиц 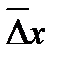и коэффициентом диффузии определяет уравнение Эйнштейна-Смолуховского:

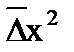= 2D × t .

Если коллоидный раствор отделен от чистого растворителя (дисперсионной среды) полупроницаемой мембраной, не пропускающей коллоидные частицы, возникает односторонняя диффузия молекул растворителя в коллоидный раствор, называемая осмосом. Осмос количественно характеризуется осмотическим давлением.

Осмотическое давление π достаточно разбавленных коллоидных растворов может быть найдено по уравнению:

,

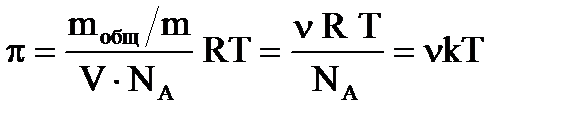где m _общ− масса растворенного вещества, m − масса одной частицы; V − объем сис­темы; N_A − постоянная Авогадро; Т − абсолютная температура; n − частичная кон­центра­ция; k − постоянная Больцмана.

К коллоидным растворам применимо и уравнение Вант-Гоффа для осмотического давления истинных растворов:

,

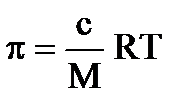где М − масса одного моля растворенного вещества; с − массовая концентрация,кг/м³.

Однако в этом случае масса 1 моль вещества заменяется массой одной частицы − мицелярной массой, определяемой по формуле:

,

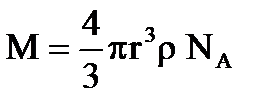где r — радиус частицы, ρ — плотность вещества.

Оптические свойства коллоидных систем тесно связаны с размерами, формой и структурой частиц дисперсной фазы.

При падении света на дисперсную систему могут наблюдаться следующие явления: прохождение света через систему, преломление или отражение света частицами дисперсной фазы, рассеяние света и поглощение света.

Размеры коллоидных частиц соизмеримы с длиной волны света. Поэтому одним из наиболее характерных оптических свойств золей является рассеяние света (опалесценция).

Закон светорассеяния выражается уравнением Рэлея:

,

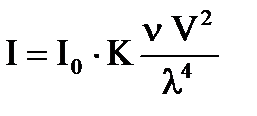где I₀ − интенсивность падающего света; I − интенсивность рассеянного света;
V − объем одной частицы; ν — частичная концентрация; λ − длина волны;
K − константа, зависящая от разности показателей преломления частицы n₁ и дисперсионной среды n₀

.

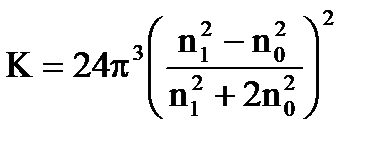Подставив в уравнение Рэлея вместо частичной n массовую концентрацию с (с= ν∙ V∙ ρ, г/л), получим:

,

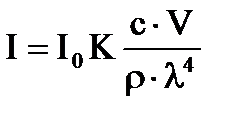т.е., светорассеяние пропорционально концентрации частиц, объему частицы и обратно пропорционально четвертой степени длины волны падающего света.

Таким образом, рассеяние коротких волн происходит более интенсивно.

Интенсивность рассеянного света тем больше, чем больше различаются показатели преломления частицы и среды (n₁− n₀); если n₁ и n₀ оди­на­ко­вы, то светорассеяния не будет.

Наряду со светорассеянием для многих коллоидных растворов характерно поглощение света определенной длины волны, чем объясняется окраска золей. Для характеристики оптических свойств коллоидных систем, способных к поглощению света, используют закон

Бугера-Ламберта-Бера:

I_пр = I₀ ∙ e^{-( k+k1)∙l∙с}

где I_0, I_пр − интенсивность падающего и прошедшего через золь света соответственно; k − коэффициент поглощения; k₁ –коэффициент рассеяния, т.е. ослабление светового потока происходит не только за счет поглощения, но и за счет рассеяния света; l − толщина слоя золя; c − концентрация золя.

Если это выражение прологарифмировать, то получим:

.

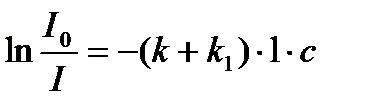Величину 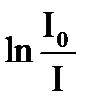называют оптической плотностью или экстинцией. Ее обозначают D_l.

В настоящее время оптические методы являются наиболее распространенными методами определения размера, формы и структуры коллоидных частиц. К ним относятся:

- ультрамикроскопия, основанная на наблюдении рассеяния света в оптическом ультрамикроскопе, позволяющем обнаруживать частицы размером до 2 ∙ 10^-8см;

- электронная микроскопия, использующая вместо световых лучей пучки быстрых электронов, позволяющая непосредственно видеть и фотографировать коллоидные частицы;

- нефелометрия − метод определения размеров коллоидных частиц или концентрации золя, основанный на измерении интенсивности светорассеяния коллоидным раствором;

- турбидиметрия − метод исследования, основанный на измерении интенсивности проходящего через коллоидную систему света, который ослабляется в результате светорассеяния.