Схемы пространственной системы сил

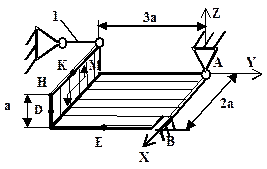Схема 1	Схема 2
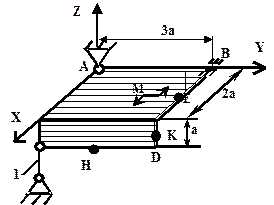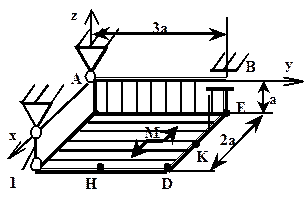Схема 3	Схема 4
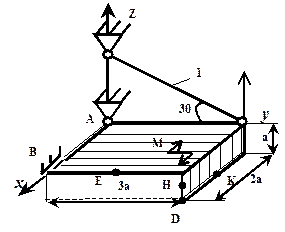Схема 5	Схема 6
Схема 7	Схема 8
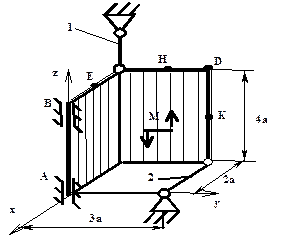Схема 9	Схема 10

Таблица 1.2.

Варианты условий пространственной системы сил

№ Номер условия		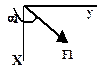		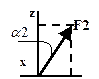	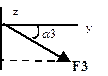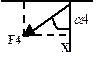Угол стержня 1 с осью
F1=6 кН	F2=8 кН	F3=10 кН	F4=12 кН
Точка приложения	a1, град	Точка приложения	a2, град	Точка приложения	a3, град	Точка приложения	a4, град	градус
			D		E				z – 90
					K		E		z – 0
	K				D				z – 0
			E				D		z – 0
	H		K						y – 90
			H		D				y – 0
					H		K		z –90
	D				K				y – 0
			D				H		y – 90
	Е		Н						x - 90
			D		E				z –30
					K		E		z –30
	K				D				z –30
			E				D		z –30
	H		K						y – 45
			H		D				y – 45
					H		K		z – 45
	D				K				y – 30
			D				H		y –120
	Е		Н						x – 60
			D		E				z – 0
					K		E		z – 60
	K				D				z – 60
			E				D		z – 60
	H		K						y – 30
			H		D				y – 90
					H		K		z – 0
	D				K				y – 60
			D				H		y – 180
	Е		Н						x – 30

ПЛОСКАЯ СИСТЕМА СИЛ

Решение задач плоской системы значительно облегчается с использованием компьютерных технологий и программы Mathcad, которые позволяют не только определить реакции в опорах, а также проверить правильность решения, но и провести анализ влияния изменяющихся по модулю или направлению силовых факторов на реакции в опорах. При этом проведение такого анализа не сопряжено с повышением трудоемкости выполнения задачи, а результаты расчета можно наглядно представить в виде графиков.

Решение задачи с нахождением уравнений искомых реакций

Жесткая рама, расположенная в вертикальной плоскости, закреплена в точке А шарнирно, а в точке В прикреплена к шарнирной опоре на катках. В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р. Все действующие на раму нагрузки и размеры показаны на рис. 2.1.

Пусть: F1=25 kH, F2=25 kH, P=18 kH, a=0.5 m, M=50 kH×m, a=60°, a3=60°, b=30°.

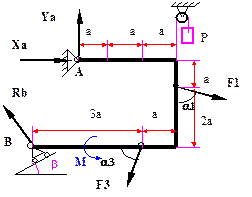Для решения задачи проведем координатные оси х, у и изобразим действующие на раму силы: F1 и F3 , а также пару сил с моментом M, натяжение троса Т (по модулю Т=Р) и реакции связей Xa, Ya, Rb (реакцию шарнирной опоры на катках направим перпендикулярно опорной плоскости).

Для полученной плоской системы сил составим три уравнения равновесия. При вычислении момента силы F относительно точки А воспользуемся теоремой Вариньона, т. е. разложим силу F на составляющие (F'=Fcosa, F''=Fsina) и учтем, что mA(F)= mA( F')+ mA( F'').

Рис.2.1 Плоская система сил

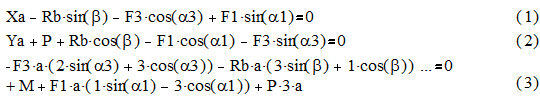В результате получим:

Совместно решая полученную систему уравнений, получим следующие аналитические зависимости (формулы) для определения каждой из реакций связей:

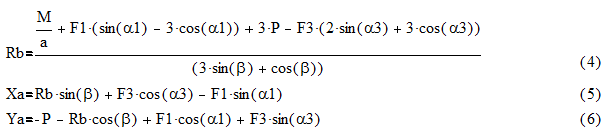
Подставляя в полученные уравнения числовые значения заданных величин, определим искомые реакции: Xa= -7,6 kH , Ya = 13,46 kH , Rb = 3,1 kH.

Знак «-» указывает, что реакция Xa направлена противоположно.