Уравнение Аррениуса (1889 г.)
k – константа скорости реакции;
А – предэкспоненциальный множитель,
Здесь А характеризует частоту столкновений реагирующих молекул.
В рамках теории активных соударений А зависит от температуры. Оценки этого параметра показывают, что изменение температуры в диапазоне от 200 °C до 300 °C приводит к изменению частоты столкновений А на 10 %.
В рамках теории активированного комплекса получаются другие зависимости А от температуры, но во всех случаях более слабые, чем экспонента.
R – универсальная газовая постоянная;
T – абсолютная температура;
Eа – энергия активации.
С ростом температуры число активных молекул возрастает и скорость химической реакции увеличивается.
Влияние температуры на скорость химических реакций описывается эмпирическим правилом Вант-Гоффа:
 |
«При повышении температуры на каждые 10 градусов скорость реакции увеличивается примерно в 2-4 раза».
( гамма - температурный коэффициент или коэффициент Вант-Гоффа).
Или:
ТЕПЛОТА (ЭНТАЛЬПИЯ) ОБРАЗОВАНИЯ
Под теплотой образования понимают тепловой эффект реакции образования 1 моля вещества из простых веществ. Стандартные теплоты образования обозначаются ΔH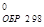 
.
Теплоты образования простых веществ, устойчивых в стандартных условиях (графит, ромбическая сера, жидкий бром, кристаллический йод, белый фосфор и др.) принимают равными 0. Стандартные теплоты образования веществ приведены в физико-химических справочниках.
Согласно закону Гесса: тепловой эффект реакции = ∑ теплот образования продукта реакции − ∑ теплот образования исходных веществ.
Для реакции вида: aA + bB + … = dD + eE + …
тепловой эффект ΔH определяется:
ΔH = ∑ΔHобр. прод. − ∑ΔHобр. исх.=(dΔH 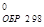. D + eΔH 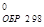E + ...) - (aΔH 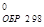A + bΔH 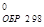B + ...)
Энтропия
Большинство процессов представляет собой два одновременно происходящих явления: передачу энергии и изменение в упорядоченности расположения частиц друг относительно друга. Частицам (молекулам, атомам, ионам) присуще стремление к беспорядочному движению, поэтому система стремится перейти из более упорядоченного состояния в менее упорядоченное. Количественной мерой беспорядка является энтропия S. Изменение энтропии ΔS в изолированной системе, переходящей из состояния (1) в состояние (2), можно определить соотношением:
ΔS = R 
,
где R – газовая постоянная.
Энтропия – это логарифмическое выражение вероятности существования системы:
ΔS = R lnW,
где W – число равновероятных микроскопических состояний, которыми можно реализовать данное макроскопическое состояние системы.
Для реакции аА + bB + … = dD + еЕ + …
ΔS = ∑ΔSпрод − ∑ΔSисх=(dΔS 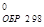. D + eΔS 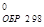E + ...) - (aΔS 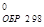A + bΔS B + ...)
Энергия Гиббса G связана с энтальпией, энтропией и Т˚: G = H – TS
или при T, р = const следует изменение: ΔG = ΔH – TΔS.
Характер изменения изобарного потенциала позволяет судить о принципиальной возможности или невозможности осуществления процесса. Условием принципиальной возможности процесса является неравенство: ΔG < 0.
Иными словами, если G в процессе реакции уменьшается, то процесс возможен, и, начавшись, он протекает самопроизвольно.
Увеличение же изобарного потенциала:
ΔG > 0
свидетельствует о невозможности осуществления процесса в данных условиях. Если же ΔG = 0, тосистема находится в состоянии химического равновесия.