Доверительный интервал

Доверительный интервал(confidence interval)характеризует достоверность математического ожидания, а именно диапазон, в котором находится искомая истинная величина при заданном доверительном уровне. Положительные и отрицательные части этогоинтервала, т.е. ниже и выше математического ожидания, называют доверительными границами (confidence limits). При симметричном распределении погрешностей относительно математического ожидании, когда эти границы равны друг другу, их называются доверительной погрешностью (confidence error). Величины доверительного интервала среднего значения обычно выражают через величину доверительной погрешности, в виде 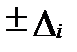и определяют уравнением:

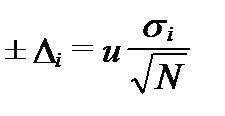, ( I‑97)

где u – квантильнормального распределения, N- число наблюдаемых значений, σ_i- стандартное отклонение полной погрешности (при N ≥ 20), т.е. прецизионности метода опробования в целом. Величина квантили зависит от вероятностного распределения и используется для определения доверительного уровня (confidence level) – P. Величина этого уровняхарактеризуетвероятность, что искомое истинное значение находится в границах данного доверительного интервала. При u =1 P= 0,68, при u = 1,96 - 0,95, при u = 3 - 0,997.

Доверительные погрешности при доверительном уровне u =1, т.е. при P= 0,68 равны:

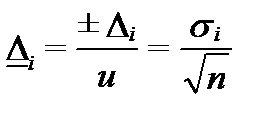(I‑98)

и называются стандартной ошибкой (standard error).

В случае логнормального распределения наблюдаемых значений стандартное отклонение полной погрешности характеризует, по своей сути, среднюю величину относительного отклонения замеренных величин от среднего (во сколько раз, а не на сколько). Поэтому доверительный интервал среднегеометричекого значения характеризует диапазон относительной доверительной погрешности (relative confidence error)±δ_i . Абсолютная и относительная доверительные погрешности связаны уравнением:

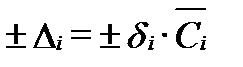. (I‑99)

В соотвествии с требованиями ГОСТ’овР ИСО 5725-1-2002 и 27384-2002 доверительные границы (нижняя и верхняя) при уровне доверия 0,95 рассматриваются в качестве норм погрешности измерений показателей свойств и состава вод, т.е. как предельные погрешности (limiting error). В ГОСТ'ах эти нормы обычно выражаются в процентах нижней границы относительной полной погрешности, величина которой растет с приближением концентрации к пределу обнаружения. Поэтому и нормы погрешности иногда даются в зависимости от величины измеряемого показателя (Таблица I-47). Согласно этим ГОСТ'ам погрешности измерения свойств и состава природных, питьевых и сточных вод не должны превышать эти нормы.

Таблица I‑47. Нормы относительной погрешности измерений свойств и состава воды согласно ГОСТ’у 27384-2002.

Величина показатля качества воды, мг/л	Нормы случайной относительной погрешности ±δ%,
В природных и сточных водах	В питьевых водах
< 0,000005
0,000005 - 0,00001
0,00001 - 0,0001
0,0001 - 0,001
0,001 - 0,01
0,01 - 0,1
0,1 - 1
1 - 10
10-100
100-500
500-1000

При доверительном уровне 0,95 доверительный интервал измерений качества природных вод зависит только от точности (полной погрешности) метода опробования и числа наблюдаемых значений:

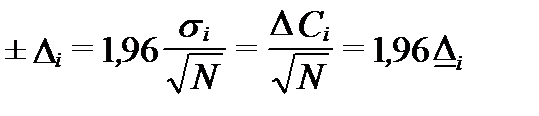. (I‑100)

В электронных таблицах MS Excel для расчета доверительного интервала при N <30 можно воспользоваться статистической функцией ДОВЕРИТ или процедурой описательной статистики в Анализе данных. В первом случае необходимо ввести доверительный уровень, т.е. значимости (Альфа), стандартное отклонение выборки и число наблюдений (Размер). В описательной статистике (Сервис, Анализ данных) необходимо ввести интервал с наблюдаемыми значениями (Входной интервал) и указать доверительный уровень (Уровень надежности).

При отсутствии контроля и параметров качества измерений, доверительный интервал определяется независимо от цели опробования по величине стандартного отклонения выборки (standard sample deviation )- s_i, величина которого определяется уравнением

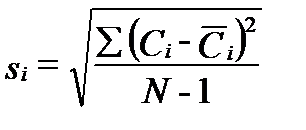, (I‑101)

где N - число наблюдаемых значений. Очевидно, что для оценки доверительного интервала в этом случае необходимо иметь, как минимум, два опробования по каждому водопункту. По мере увеличения N значение s_i стремится к σ_i.

Для стандартного отклонения малой выборки вместо квантилиu используется коэффициент Стьюдента (Student's factor) t_t, величина которого зависит от степени свободы, равной N-1, и доверительного уровня (см. таблицу I-46) . Поэтому при отсутствии параметров погрешности доверительный интервал результатов измерения определяют уравнением:

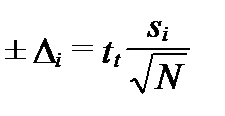. ( I‑102)

При характеристке доверительных интервалов показателей потребительских качеств воды в уравнении I-99 используют величины внутрилабораторной полной абсолютной погрешности 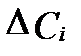или стандартного отклонения σ_i методов анализа. При определении доверительного интервала показателей качества воды в пластовых условиях используются те же параметры, но для всей методики опробования, полученные с помощью контрольных проб.

При наличии только одного измерения доверительный интервал имеет самый широкий диапазон ± 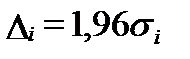. Чем больше число повторных опробований и наблюдаемых значений, тем меньше доверительный интервал. Но его величина может быть существенно уменьшена только при 2, 3 или 4 наблюдаемых значениях. Дальнейшее увеличение числа опробований экономически не целесообразно.

Полная погрешность опробования позволяет оценить оптимальное число повторных опробований одной точки для достижения требуемого доверительного интервала. Согласно уравнению (I-100), при доверительном уровне 0,95 для достижения заданного доверительного интервала 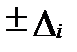минимальное число повторных опробований равно:

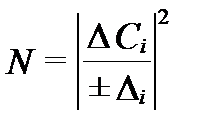. I‑103

Величины результатов измерений ( 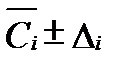) систематизируются в виде реляционной базы данных (database). Такая база результатов измерений представляется в виде матрицы, в которой строки соответствуют объектам опробования, а столбцы - признакам этих объектов (их привязка на местности, параметры показателей обстановки, свойств и состава). В электронных таблицах этой базы данных каждый объект опробования имеет только один ряд усреденных показателей. Такие базы данных предусмотрены практически во всех специальных гидрохимических программах (AquaChem, The Geochemist's Workbench, GWB Essentials, HydroGto, SOXXXX, NETPATH, PHREEQC, PHREEQCI, PHRQPITZ, WATEQ4F, MINTEQA2 и др.). Их формат, перечень учитываемых компонентов и набор параметров в таких базах обычно достаточно индивидуальны. Однако каждый объект опробования имеет координаты привязки на местности, которые позволяют строить карты исходных данных (post maps)и фактического материала (facts maps). На эти карты наносятся все точки опробования с характеристикой условным знаком типа водного объекта (источник, колодец, скважина и т.д.) и величины исследуемого параметра. На сводной карте фактического материала у каждой точки опробования дается перечень выполненных исследований, т.е. список параметров, по которым имеются результаты измерений. Эти базы данных с системой управления служат основанием для гидрогехимического описания опробованного гидрогеологического объекта и моделирования гидрохимических процессов.

Наблюдаемые значения(observed value) представляют собой все результаты отдельных измерений показателей свойств и состава проб подземных вод. Эти измерения выполнены либо непосредственно в поле, либо в пробах воды разными методами, разными организациями, часто в разные годы. Большую и наиболее ответственную часть наблдаемых значений составляют результаты химических анализов. Эти анализы характеризуют состав, как рабочих проб на разные показатели, так и контрольных проб. Эти данные требуют, прежде всего, тщательной проверки и систематизации.