Тепловой баланс горения
Тепловым эффектом реакции называется количество теплоты, которое выделяется или поглощается системой в ходе реакции [2].
Теплосодержание системы определяется теплотой образования компонентов системы (продуктов горения и исходного вещества). Таким образом тепловой эффект реакции можно записать:
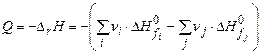 , (3.1)
, (3.1)
где 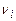 ,
, 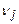 - стехиометрические коэффициенты продуктов реакции и исходных веществ;
- стехиометрические коэффициенты продуктов реакции и исходных веществ; 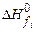 ,
, 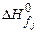 - стандартные энтальпии образования продуктов реакции и исходных веществ. Теплота образования
- стандартные энтальпии образования продуктов реакции и исходных веществ. Теплота образования 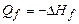 . Здесь индекс
. Здесь индекс 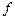 означает formation (образование), а ноль, что величина относится к стандартному состоянию вещества.
означает formation (образование), а ноль, что величина относится к стандартному состоянию вещества.
Теплота образования веществ определяется по справочникам или рассчитывается исходя из структуры вещества.
Теплотой сгорания называется количество тепла, выделяющееся при полном сгорании единицы количества вещества при условии, что начальные и конечные продукты находятся в стандартных условиях.
Различают:
· молярную 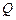 — для одного моля (кДж/моль),
— для одного моля (кДж/моль),
· массовую 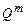 − для одного килограмма (кДж/кг),
− для одного килограмма (кДж/кг),
· объемную 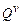 − для одного кубического метра вещества (кДж/м³) теплоту сгорания.
− для одного кубического метра вещества (кДж/м³) теплоту сгорания.
В зависимости от агрегатного состояния воды, образовавшейся в процессе горения, различают высшую 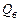 и низшую
и низшую 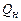 теплоту сгорания.
теплоту сгорания.
Высшей теплотой сгорания называется количество тепла, которое выделяется при полном сгорании единицы количества горючего вещества, включая тепло конденсации водяных паров.
Низшей теплотой сгорания называется количество тепла, которое выделяется при полном сгорании единицы количества горючего вещества при условии, что вода в продуктах горения находится в газообразном состоянии.
Молярную теплоту сгорания рассчитывают в соответствии с законом Гесса. Для пересчета молярной теплоты сгорания 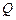 в массовую
в массовую 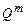 можно использовать формулу:
можно использовать формулу:
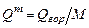 ,
, 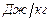 , (3.2)
, (3.2)
где 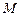 - молярная масса горючего вещества,
- молярная масса горючего вещества, 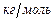 .
.
Для веществ в газообразном состоянии при пересчете из стандартной теплоты сгорания 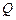 в объемную
в объемную 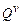 используют формулу:
используют формулу:
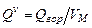 ,
, 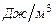 , (3.3)
, (3.3)
где 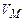 - молярный объем газа, который при стандартных условиях равен
- молярный объем газа, который при стандартных условиях равен 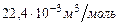 .
.
Достаточно точные результаты для сложных горючих веществ или смесей дает формула Менделеева для высшей теплоты сгорания:
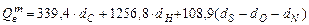 , (3.4)
, (3.4)
где 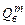 ,
, 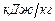 ;
; 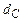 ,
, 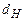 ,
, 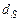 ,
, 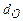 ,
, 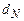 - содержание в горючем веществе соответственно углерода, водорода, серы, кислорода и азота в масс. процентах.
- содержание в горючем веществе соответственно углерода, водорода, серы, кислорода и азота в масс. процентах.
Для низшей теплоты сгорания
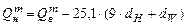 , (3.5)
, (3.5)
где 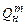 ,
, 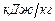 ;
; 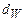 - содержание влаги в горючем веществе в масс. процентах.
- содержание влаги в горючем веществе в масс. процентах.
Расчет теплоты сгорания горючих смесей выполняют по формуле
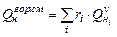 , (3.6)
, (3.6)
где 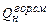 - низшая теплота сгорания горючей смеси,
- низшая теплота сгорания горючей смеси, 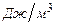 ;
;  - объемная доля
- объемная доля  -ого горючего в смеси;
-ого горючего в смеси; 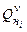 - низшая теплота сгорания
- низшая теплота сгорания  -ого горючего в смеси,
-ого горючего в смеси, 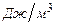 .
.
Расчет теплоты сгорания газо-воздушных смесей проводят с использованием формулы
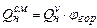 , (3.7)
, (3.7)
где 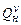 - низшая теплота сгорания горючего вещества,
- низшая теплота сгорания горючего вещества, 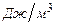 ;
; 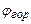 - концентрация горючего вещества в газо-воздушной смеси, объемная доля;
- концентрация горючего вещества в газо-воздушной смеси, объемная доля; 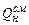 - теплота сгорания газо-воздушной смеси,
- теплота сгорания газо-воздушной смеси, 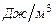 .
.
Теплоёмкость тела называется физическая величина, определяющая отношение бесконечно малого количества теплоты 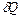 , полученного телом, к соответствующему приращению его температуры
, полученного телом, к соответствующему приращению его температуры 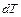
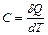 . (3.8)
. (3.8)
Количество теплоты, подведенное к телу или отведенное от него, всегда пропорционально количеству вещества.
Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. Количество вещества может быть измерено в килограммах, кубических метрах и молях. Поэтому различают массовую, объёмную и молярную теплоёмкость.
Обозначим:
· 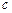 - молярная теплоемкость,
- молярная теплоемкость, 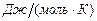 . Это количество теплоты, которое нужно подвесит к 1 молю вещества, что его температура повысилась на 1 Кельвин;
. Это количество теплоты, которое нужно подвесит к 1 молю вещества, что его температура повысилась на 1 Кельвин;
· 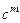 - массовая теплоемкость,
- массовая теплоемкость, 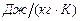 . Это количество теплоты, которое нужно подвесит к 1 килограмму вещества, что его температура повысилась на 1 Кельвин;
. Это количество теплоты, которое нужно подвесит к 1 килограмму вещества, что его температура повысилась на 1 Кельвин;
· 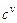 - объемная теплоемкость,
- объемная теплоемкость, 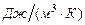 . Это количество теплоты, которое нужно подвесит к 1 кубическому метру вещества, что его температура повысилась на 1 Кельвин.
. Это количество теплоты, которое нужно подвесит к 1 кубическому метру вещества, что его температура повысилась на 1 Кельвин.
Связь между молярной и массовой теплоемкостями выражается формулой
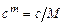 , (3.9)
, (3.9)
где 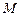 - молярная масса вещества. Объемная теплоемкость выражается через молярную следующим образом
- молярная масса вещества. Объемная теплоемкость выражается через молярную следующим образом
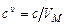 , (3.10)
, (3.10)
где  - молярный объем газа при нормальных условиях.
- молярный объем газа при нормальных условиях.
Теплоемкость тела зависит от процесса, в ходе которого осуществляется подвод теплоты.
Теплоемкостью тела при постоянном давлении 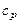 называют отношение удельного (на 1 моль вещества) количества теплоты, подведенной в изобарном процессе, к изменению температуры тела.
называют отношение удельного (на 1 моль вещества) количества теплоты, подведенной в изобарном процессе, к изменению температуры тела.
Теплоемкостью тела при постоянном объеме 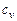 называют отношение удельного (на 1 моль вещества) количества теплоты, подведенной в изохорном процессе, к изменению температуры тела.
называют отношение удельного (на 1 моль вещества) количества теплоты, подведенной в изохорном процессе, к изменению температуры тела.
Теплоемкость идеальных газов равна
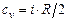 , (3.11)
, (3.11)
где  - число степеней свободы молекулы. Связь между изобарной и изохорной теплоёмкостями идеальных газов определяется уравнением Майера
- число степеней свободы молекулы. Связь между изобарной и изохорной теплоёмкостями идеальных газов определяется уравнением Майера
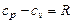 , (3.12)
, (3.12)
где 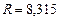
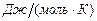 -универсальная газовая постоянная.
-универсальная газовая постоянная.
Теплоемкость веществ в твердой фазе для условий близких к нормальным по закону Дюлонга-Пти равна
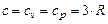 . (3.13)
. (3.13)
Вследствие того что теплоемкость зависит от температуры, расход теплоты для одинакового повышения температуры меняется (рис. 3.1).
Истинной теплоемкостью называют теплоемкость, которая при определенном термодинамическом процессе, выражается следующей формулой
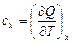 , (3.14)
, (3.14)
где 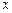 - обозначает процесс, при котором измеряется теплоемкость. Параметр
- обозначает процесс, при котором измеряется теплоемкость. Параметр 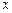 может принимать значения
может принимать значения  ,
, 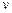 и др.
и др.
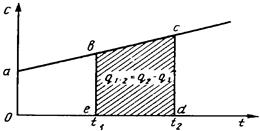
Рис. 3.1. Зависимость теплоемкости от температуры
Средней теплоемкостью называется отношение количества теплоты, сообщаемое телу в заданном процессе, к изменению температуры при условии, что разность температур является конечной величиной. При известной зависимости истинной теплоемкости от температуры 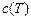 среднюю теплоемкость на интервале температур от
среднюю теплоемкость на интервале температур от 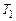 до
до 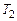 можно найти с помощью теоремы о среднем значении
можно найти с помощью теоремы о среднем значении
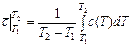 , (3.15)
, (3.15)
где 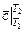 - средняя теплоемкость,
- средняя теплоемкость, 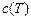 -истинная теплоемкость.
-истинная теплоемкость.
В экспериментальных исследованиях теплоемкости веществ зачастую находят среднюю теплоемкость как функцию верхнего предела, при фиксированном значении нижнего предела, который принимают равным 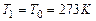
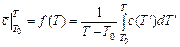 . (3.16)
. (3.16)
Зависимости средних теплоемкостей газов от температуры верхнего предела приведены в таблице 3.1.
Теплоемкость газовой смеси зависит от состава смеси и теплоемкостей компонент. Обозначим: 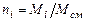 - молярная доля
- молярная доля  компонента в смеси;
компонента в смеси; 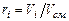 - объемная доля;
- объемная доля; 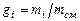 - массовая доля. Здесь
- массовая доля. Здесь 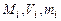 - количество
- количество  -ого компонента в моля, м3, кг соответственно. Теплоемкость газовой смеси можно определить по формулам
-ого компонента в моля, м3, кг соответственно. Теплоемкость газовой смеси можно определить по формулам
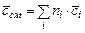 ,
, 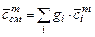 ,
, 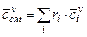 , (3.17)
, (3.17)
где 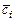 ,
, 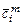 ,
, 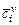 - средние молярная, массовая и объемная теплоемкости
- средние молярная, массовая и объемная теплоемкости  -ого компонента смеси.
-ого компонента смеси.
Таблица 3.1.
| Название газа | Формулы для определения средних мольных теплоемкостей отдельных газов при постоянном объеме, Дж/(моль·град), для температур, 0С | |
| от 0 до 1500 | от 1501 до 2800 | |
| Воздух | 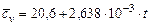 | 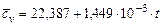 |
Кислород 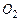 | 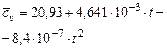 | 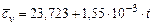 |
Азот 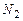 | 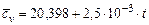 | 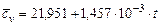 |
Водород  | 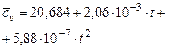 | 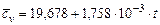 |
Оксид углерода  | 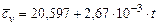 | 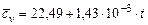 |
Углекислый газ 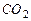 | 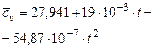 | 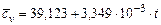 |
Водяной пар 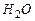 | 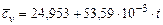 | 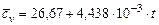 |
В тепловых машинах и двигателях, вначале каждого цикла в камеру сгорания подается порция свежей смеси, которую называют свежим зарядом. Однако, как правило, в камере сгорания остаются отработавшие газы от предыдущего цикла.
Коэффициентом остаточных газов называется отношение
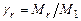 , (3.18)
, (3.18)
где 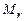 - количество моль остаточных газов,
- количество моль остаточных газов, 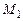 - количество моль свежего заряда. Смесь в камере сгорания остаточных газов со свежим зарядом называется рабочей смесью. Теплоемкость рабочей смеси рассчитывается по формуле
- количество моль свежего заряда. Смесь в камере сгорания остаточных газов со свежим зарядом называется рабочей смесью. Теплоемкость рабочей смеси рассчитывается по формуле
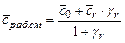 , (3.19)
, (3.19)
где 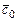 ,
, 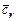 - средние теплоемкости свежего заряда и остаточных газов при температуре рабочей смеси;
- средние теплоемкости свежего заряда и остаточных газов при температуре рабочей смеси; 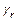 - коэффициент остаточных газов.
- коэффициент остаточных газов.
Тепло, выделяющееся в зоне горения, расходуется на нагрев продуктов сгорания и тепло потери (к последним относятся предварительный нагрев горючего вещества и излучение из зоны горения в окружающую среду). Максимальная температура, до которой нагреваются продукты горения, называется температурой горения.
В зависимости от условий, в которых протекает процесс горения различают калориметрическую, адиабатическую, теоретическую, и действительную температуры горения [12].
Под калориметрической температурой горения понимают температуру, до которой нагреваются продукты горения при соблюдении следующих условий:
· все тепло, выделившееся в процессе реакции, идет на нагревание продуктов горения;
· происходит полное сгорание стехиометрической горючей смеси ( 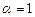 );
);
· в процессе образования продуктов горения не происходит их диссоциация;
· горючая смесь находится при начальной температуре 273К и давлении 101,3 кПа.
Адиабатическая температура горения определяется для не стехиометрической горючей смеси ( 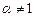 ).
).
Теоретическая температура горения отличается от калориметрической тем, что в расчетах учитываются потери тепла в следствии диссоциации продуктов горения.
Действительная температура горения - это температура, до которой нагреваются продукты горения в реальных условиях.
Рассмотрим расчет только калориметрической и адиабатической температуры горения с небольшой поправкой. Будем считать, что начальная температура исходной смеси отличается от 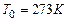 . Обозначим
. Обозначим 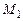 и
и 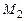 количества моль рабочей смеси и смеси продуктов горения. Тогда тепловой баланс горения при постоянном давлении можно записать таким образом
количества моль рабочей смеси и смеси продуктов горения. Тогда тепловой баланс горения при постоянном давлении можно записать таким образом
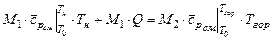 , (3.20)
, (3.20)
где 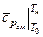 ,
, 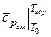 - средние теплоемкости исходной смеси и продуктов горения;
- средние теплоемкости исходной смеси и продуктов горения; 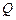 - теплота, выделяющаяся при сгорании 1 моля рабочей смеси,
- теплота, выделяющаяся при сгорании 1 моля рабочей смеси, 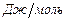 ;
; 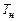 и
и 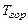 - температуры рабочей смеси и продуктов горения соответственно. По отношению к одному молю рабочей смеси формулу (3.20) можно представить в виде
- температуры рабочей смеси и продуктов горения соответственно. По отношению к одному молю рабочей смеси формулу (3.20) можно представить в виде
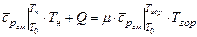 , (3.21)
, (3.21)
где 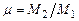 - коэффициент молекулярного изменения состава смеси. Из уравнения теплового баланса находят калориметрическую и адиабатическую температуры горения.
- коэффициент молекулярного изменения состава смеси. Из уравнения теплового баланса находят калориметрическую и адиабатическую температуры горения.
При взрыве объем исходной смеси можно считать неизменным. Для расчета температуры взрыва достаточно определить температуру сгорания в процессе с постоянным объемом
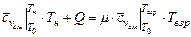 . (3.22)
. (3.22)
Давление при взрыве можно найти с помощью уравнения Клайперона-Менделеева, учитывая, что объем в процессе не меняется.
Практическая работа №3
«Расчет теплоты сгорания веществ»
Цель: Усвоить основные понятия энергетического баланса процессов горения. Научиться делать расчет теплоты сгорания для разного типа горючего вещества (индивидуальные вещества и смеси; сложные вещества, представленные элементарным составом).
Расчетные формулы и алгоритмы
1. Для расчета теплоты сгорания индивидуальных веществ используется формула (3.1). Сначала составляют уравнение реакции горения, с помощью которого определяют стехиометрические коэффициенты и продукты. Затем по таблице (см. таблицу 3.1) находят стандартных энтальпии образования исходных веществ и продуктов реакции. Найденные параметры, подставляются в формулу (3.1) и вычисляется теплота сгорания горючего вещества.
2. Теплоту сгорания сложных веществ находят по формулам Д. И. Менделеева (3.4) и (3.5). Для выполнения расчета необходимо знать только массовые доли элементов в процентах. Теплота сгорания вычисляется в кДж/кг.
3. Для расчета горючих смесей пользуются формулами (3.1) – (3.6). Сначала находят низшую теплоту сгорания каждого горючего газа как индивидуального вещества по формуле (3.2) или как сложного вещества по формулам (3.4),(3.5). Для перехода к объемной теплоте сгорания применяют формулы (3.2),(3.3). Завершают расчет вычислением низшей теплоты сгорания смеси горючих по формуле (3.6).
4. Для определения теплоты сгорания 1 м3 газо-воздушной смеси вычисляют объемную долю горючих газов в присутствии воздуха, количество которого зависит от  . Затем с помощью формулы (3.7) вычисляют теплоту сгорания газо-воздушной смеси.
. Затем с помощью формулы (3.7) вычисляют теплоту сгорания газо-воздушной смеси.
Пример 3.1. Определить низшую теплоту сгорания ацетилена.
Решение. Запишем уравнение горения ацетилена.
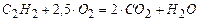
В соответствии с уравнением стехиометрические коэффициенты равны 
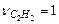 ,
, 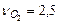 ,
, 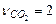 ,
, 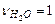 . Используя приложение 3.1 находим стандартные энтальпии образования веществ реакции:
. Используя приложение 3.1 находим стандартные энтальпии образования веществ реакции: 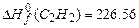
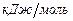 ,
, 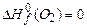
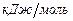 ,
, 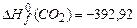
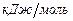 ,
, 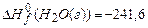
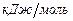 . По формуле (3.1) вычисляем низшую теплоту сгорания ацетилена
. По формуле (3.1) вычисляем низшую теплоту сгорания ацетилена
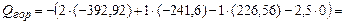
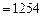
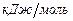 .
.
Для расчета количества тепла, выделяющегося при горении 1 м3 ацетилена, необходимо полученную величину разделить на молярный объем в стандартных условия (3.3):
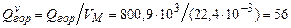
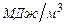 .
.
Ответ: 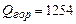
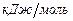 ;
; 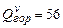
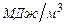
Пример 3.2. Рассчитать низшую теплоту сгорания органической массы состава:  - 62%,
- 62%, 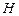 - 8%,
- 8%, 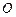 - 28%,
- 28%, 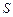 - 2%.
- 2%.
Решение. По формулам Менделеева (3.4) и (3.5) находим
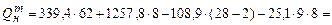
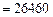
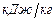 .
.
Ответ: 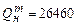
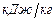 .
.
Пример 3.3. Определить теплоту сгорания газовой смеси, состоящей из 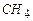 - 40%,
- 40%, 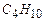 - 20%,
- 20%, 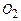 - 15%,
- 15%, 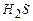 - 5%,
- 5%, 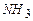 - 10%,
- 10%, 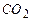 - 10%.
- 10%.
Решение. Из этих газов горючими являются 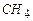 ,
, 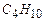 ,
, 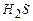 ,
, 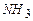 . Выпишем для каждого горючего уравнение реакции с кислородом:
. Выпишем для каждого горючего уравнение реакции с кислородом:
(1) 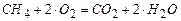 ;
;
(2) 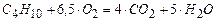 ;
;
(3) 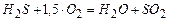 ;
;
(4) 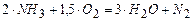 .
.
Стандартные энтальпии образования веществ находим с помощью табличных данных таблице 3.2.
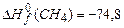 ;
; 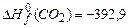 ;
; 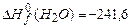 ;
; 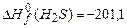 ;
; 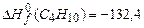 ;
; 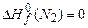 ;
; 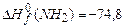 ;
; 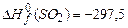
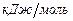 .
.
По формуле (3.1) в соответствии с уравнениями горения (1)-(4) находим теплоту сгорания, 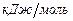 :
:
(1) 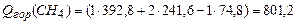 ;
;
(2) 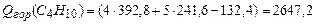 ;
;
(3) 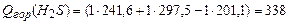 ;
;
(4) 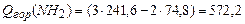 .
.
Для смеси горючих газов используем формулу (3.6), учитывая, что молярные и объемные доли совпадают. В результате вычислений получаем низшую теплоту сгорания смеси газов
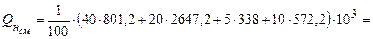
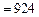
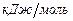 .
.
При сгорании 1 м3 такой смеси газов выделяется теплота равная
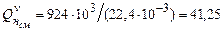
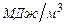 .
.
Ответ: 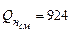
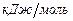 ;
; 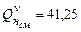
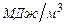 .
.
Пример 3.4. Рассчитать низшую теплоту сгорания пропан-воздушной смеси, если коэффициент избытка воздуха 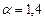 .
.
Решение. Записываем уравнение горения пропана
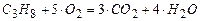 .
.
В соответствии в уравнением реакции на 1 м3 пропана должно приходиться 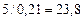 м3 воздуха для стехиометрической смеси. Учитывая, что
м3 воздуха для стехиометрической смеси. Учитывая, что 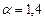 на 1 м3 пропана фактически расходуется
на 1 м3 пропана фактически расходуется 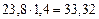 м3 воздуха. Таким образом, в 1 м3 в пропан-воздушной смеси объемная доля пропана составит
м3 воздуха. Таким образом, в 1 м3 в пропан-воздушной смеси объемная доля пропана составит
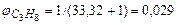 .
.
Низшую теплоту сгорания пропана найдем по формуле (3.1). Стандартная энтальпия образования пропана может быть определена по таблице 3.2.
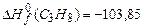
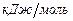
Теплота сгорания пропана равна
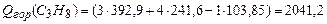
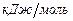 ,
,
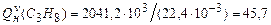
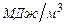 .
.
Низшую теплоту сгорания пропан-воздушной смеси можно определить по формуле (3.7)
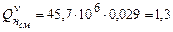
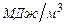 .
.
Ответ: 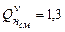
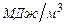 .
.
Контрольные задачи
3.1. Рассчитать высшую 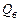 и низшую
и низшую 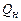 теплоту сгорания индивидуальных веществ. Параметры для расчета, в зависимости от варианта, приведены в таблице 3.3.
теплоту сгорания индивидуальных веществ. Параметры для расчета, в зависимости от варианта, приведены в таблице 3.3.
3.2. Рассчитать низшую 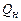 теплоту сгорания веществ сложного состава. Параметры для расчета, в зависимости от варианта, приведены в таблице 3.4.
теплоту сгорания веществ сложного состава. Параметры для расчета, в зависимости от варианта, приведены в таблице 3.4.
3.3. Какое количество вещества  кг можно нагреть от температуры
кг можно нагреть от температуры 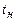 до
до 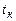 0С при сжигании
0С при сжигании 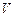 м3 горючей смеси. Параметры для расчета, в зависимости от варианта, приведены в таблице 3.5. Теплоемкость вещества найти с использованием справочников.
м3 горючей смеси. Параметры для расчета, в зависимости от варианта, приведены в таблице 3.5. Теплоемкость вещества найти с использованием справочников.
Таблица 3.2. Стандартная энтальпия образования
| Вещество и состояние | 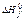 ( ( 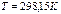 ), ), 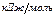 | Вещество и состояние | 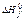 ( ( 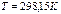 ), ), 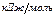 |
| Al2O3 (кр) | -1675,7 | FeO (кр) | -265 |
| Al2O3(аморф) | -1602 | Fe(OH)2 (кр) | -562 |
| B (г) | 561,6 | Fe(OH)2 (кр) | -562 |
| B2 (г) | 845,2 | Fe(OH)3 (кр) | -827 |
| B (кр) | Fe2O3 (кр) | -822 | |
| B2O3 (кр) | -1272,9 | Fe3O4 (кр) | -1117,13 |
| B2O3 (аморф) | -1254,0 | H2 (г) | |
| B2H6 (г) | H (г) | 217,98 | |
| B5H9 (г) | H+ (г) | 1536,21 | |
| B5H9 (ж) | H- (г) | 139,03 | |
| B10H14 (г) | Mg (кр) | ||
| C (г) | 715,1 | MgO (кр) | -601,5 |
| C (к, алмаз) | 1,83 | Mg(OH)2 (кр) | -924,7 |
| C (к, графит) | MgСO3 (кр) | -1095,85 | |
| CH3OH (г) | -202,0 | N2 (г) | |
| CH3OH (ж) | -239,45 | N (г) | 472,71 |
| CH4 (г) | -74,81 | NH3 (г) | -46,2 |
| CO (г) | -110,52 | NH3 (ж) | -69,87 |
| CO2 (г) | -393,51 | NO (г) | 90,2 |
| C2H2 (г) | 226,0 | NO2 (г) | 33,5 |
| C2H4 (г) | 52,5 | N2H4 (г) | 95,3 |
| C2H6 (г) | -84,7 | N2O5 (кр) | -42,7 |
| C2H5OH (г) | -234,6 | N2O (г) | 82,01 |
| C2H5OH (ж) | -276,9 | N2O4 (г) | 9,6 |
| C6H6 (ж) | 49,03 | N2O4 (ж) | -19,0 |
| C6H12 (ж) | -156,23 | HNO3 (ж) | -173,00 |
| HCN (г) | 134,7 | HNO3 (г) | -133,91 |
| HNCS (г) | 127,61 | Ni (кр) | |
| CS2 (г) | 116,7 | NiO (кр) | -239,74 |
| CS2 (ж) | 88,70 | NiS (кр) | -79,50 |
| Fe (кр) | NiSO4 (кр) | -873,49 | |
| NiS (кр) | -79,50 | TiO2 (к, рутил) | -943,9 |
| O2 (г) | TiO2 (к, анатаз) | -933,03 | |
| O (г) | 249,2 | Zr (кр.) | |
| O+ (г) | 1568,78 | Zr(OH)4 (кр) | -1661 |
| O- (г) | 101,43 | ZrO2 (кр) | -1100,6 |
| O3 (г) | 142,2 | C3H4 (г) | 192,13 |
| OH- (г) | -134,5 | C3H6 (г) | 20,41 |
| H2O (кр) | -291,85 | C3H8 (г) пропан | -103,85 |
| H2O (г) | -241,82 | C4H6 (г) | 162,21 |
| H2O (ж) | -285,83 | C4H8 (г) 1-бутен | -0,13 |
| H2O2 (ж) | -187,78 | C4H8 (г) циклобутан | 26,65 |
| H2O2 (г) | -135,88 | C4H10 (г) бутан | -126,15 |
| S (к, монокл) | 0,377 | C5H12 (г) пентан | -173,33 |
| S (к, ромб) | C5H12 (ж) | -179,28 | |
| S (г) | 278,81 | C6H6 (ж) бензол | 49,03 |
| SO2 (г) | -296,90 | C6H6 (г) бензол | 82,93 |
| SO3 (г) | -395,8 | C6H12 циклогексан | -156,23 |
| SO3 (ж) | -439,0 | C6H14 (ж) гексан | -198,82 |
| H2S (г) | -20,9 | C6H14 (г) гексан | -167,19 |
| H2SO4 (ж) | -814,2 | C7H8 (ж) толуол | 12,01 |
| Si (кр.) | C7H8 (г) толуол | 50,00 | |
| SiC (кр.) | -63 | C7H16 (ж) гептан | -224,54 |
SiO2 (к,  ) ) | -910,94 | C7H16 (г) гептан | -187,78 |
| SiO2 (стекл) | -903,49 | C8H6 (г) этинилбензол | 327,27 |
| Ti (кр) | C8H10 (ж) этилбензол | -12,48 | |
| C8H18 (г) октан | -208,45 | C4H10O (ж) бутанол | -325,56 |
| C10H8 (кр) нафталин | 78,07 | C4H10O (г) бутанол | -274,43 |
| C10H8 (ж) нафталин | C4H10O (ж) диэтиловый эфир | -279,49 | |
| C10H8 (г) нафталин | 150,96 | C4H10O(г) диэтиловый эфир | -252,21 |
| C12H10 (ж) дифенил | 119,32 | C5H12O (ж) амиловый спирт | -357,94 |
| C12H10 (г) дифенил | 182,08 | C5H12O (г) амиловый спирт | -302,38 |
| CH4O (ж) метанол | -238,57 | CH6N2 (ж) метилгидразин | 53,14 |
| CH4O (г) метанол | -201,00 | CH6N2 (г) метилгидразин | 85,35 |
| C2H4O2 (ж) уксусная кислота | -484,09 | C5H5N (ж) пиридин | 99,96 |
| C2H4O2 (г) уксусная кислота | -434,84 | C5H5N (г) пиридин | 140,16 |
| C2H6O (ж) этанол | -276,98 | C6H5NO2 (ж) нитробензол | 15,90 |
| C2H6O (г) этанол | -234,80 | C6H7N (ж) анилин | 31,09 |
| C2H6O2 (ж.) этиленгликоль | -454,90 | C6H7N (г) анилин | 86,86 |
| C2H6O2 (г) этиленгликоль | -389,32 | C2H6S2 (ж) диметилдисульфид | -62,59 |
| C3H6O (ж) ацетон | -248,11 | C2H6S2 (г) диметилдисульфид | -24,14 |
| C3H6O (г) ацетон | -217,57 | C4H4S (ж) тиофен | 81,04 |
| C3H8O (ж) 1-пропанол | -304,55 | C4H4S (г) тиофен | 115,73 |
| C3H8O (г) 1-пропанол | -257,53 |
Таблица 3.3. Параметры к контрольной задаче №3.1
| Вариант | Условие | Вариант | Условие | Вариант | Условие |
| 1. | CH3OH | 11. | C4H8 | 21. | C8H18 |
| 2. | C2H5OH | 12. | C4H10 | 22. | C10H8 |
| 3. | NH3 | 13. | C3H8 | 23. | C12H10 |
| 4. | SO3 | 14. | C7H8 | 24. | CH4O |
| 5. | HNO3 | 15. | C7H16 | 25. | C2H4O2 |
| 6. | C3H4 | 16. | C5H12 | 26. | C2H6O |
| 7. | H2S | 17. | C6H12 | 27. | C3H6O |
| 8. | C5H5N | 18. | C6H14 | 28. | C4H10O |
| 9. | С2H5O | 19. | C8H6 | 29. | CH6N2 |
| 10. | C3H6 | 20. | C8H10 | 30. | C6H7N |
Таблица 3.4. Параметры к контрольной задаче №3.2 (W - влага)
