Направление течения химических процессов

При изучении химических процессов прежде всего необходимо установить их принципиальную осуществимость, оценить возможность или невозможность их самопроизвольного протекания при заданных условиях.

4.5.1. САМОПРОИЗВОЛЬНЫЕ ПРОЦЕССЫ

Самопроизвольным называется процесс, который осуществляется без затраты работы (энергии) извне. Так, самопроизвольно камни скатываются с горы, теплота передается от более нагретого тела к менее нагретому, а химические реакции достигают состояния равновесия. В обратном направлении самопроизвольный процесс идти не может.

По-видимому, протекание рассмотренных и других процессов определяется какой-то причиной или, как принято говорить, движущей силой. Одной из составляющих (причем наиболее значимой) движущей силы всех (в том числе и химических) самопроизвольно идущих процессов является тенденция к понижению энергии системы. При падении камень теряет свою потенциальную энергию, которая в итоге (в момент его удара о землю) превращается в тепловую энергию окружающей среды. Экзотермические реакции, при протекании которых выделяется теплота, сопровождаются уменьшением химической потенциальной энергии. Экзотермические реакции, как правило, идут самопроизвольно.

Однако тенденция к достижению минимальной энергии не является единственным фактором, определяющим направление самопроизвольного процесса. На это указывает возможность самопроизвольного протекания не только экзотермических, но и эндотермических реакций. Так, например, самопроизвольно идут следующие эндотермические процессы:

- растворение хлорида калия в воде:

KCl_(т) 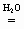KCl_(р) ; DH°(298 К) = 19 кДж/моль;

- плавление льда при комнатной температуре:

H₂O_(т) = H₂O_(ж) ; DH°(298 K) = 6 кДж/моль;

- испарение воды:

H₂O_(ж) = H₂O_(г) ; DH°(298 K) = 44 кДж/моль

и другие. В то же время в стандартных условиях невозможно осуществить экзотермический процесс синтеза, например, н-гептана C₇H₁₆, протекающего по уравнению:

7C_{(графит)} + 8H_2(г) = C₇H_16(ж); DH°(298 K) = -224,39 кДж.

Таким образом, тепловой эффект реакции не является критерием направления течения процесса. Другими словами, первый закон термодинамики не позволяет судить о способности химических процессов к самопроизвольному протеканию.

4.5.2 ЭНТРОПИЯ

В природе протекание большинства процессов, в том числе и химических, сопровождается не только энергетическими эффектами, но и изменением в упорядочении расположения частиц относительно друг друга. Рассмотренные выше примеры превращений имеют одно общее свойство: в каждом случае состояние продуктов характеризуется большей хаотичностью, или неупорядоченностью, чем состояние реагентов. Растворение хлорида калия сопровождается нарушением регулярности в расположении частиц в узлах кристаллической решетки - возникает беспорядочное распределение ионов в растворе. Молекулы воды, образующие кристалл льда, прочно удерживаются в его кристаллической решетке. При плавлении льда молекулы H₂O начинают свободно перемещаться относительно друг друга. Высокоупорядоченная кристаллическая структура заменяется неупорядоченной структурой жидкости. В процессе испарения структура жидкости, представленная ассоциатами из ее молекул, заменяется отдельными молекулами, движущимися независимо (в газовой фазе).

Таким образом, частицам (молекулам, атомам, ионам и др.) присуще стремление к беспорядочному движению, поэтому система стремится перейти из более упорядоченного состояния в менее упорядоченное. Количественной мерой неупорядоченности (беспорядка) системы является термодинамическая функция состояния системы - энтропия (S, Дж/(моль·K)). Чем в большей мере выражен беспорядок в системе, тем больше ее энтропия. Следовательно, еще одной составляющей движущей силы самопроизвольно протекающих процессов является тенденция к увеличению энтропии системы.

4.5.3. РАСЧЕТ ИЗМЕНЕНИЙ ЭНТРОПИИ

Энтропию веществ принято относить к стандартным условиям (T = 298,15 K и p = 101,3 кПа). Энтропию при этих условиях называют стандартной энтропией и обозначают S°(298 K). Значения стандартных энтропий для многих веществ являются справочными данными.

Принято, что энтропия идеально правильно построенных кристаллов при T = 0 К равна нулю (в такой системе полностью устраняется всякая неупорядоченность, положение частиц в узлах кристаллической решетки характеризуется идеальным порядком). Поэтому перед обозначением стандартной энтропии вещества (B) S°(298 K (B)) отсутствует знак D . Для каждого индивидуального вещества (простого или сложного) значение S(Т) > 0 при любой температуре, отличной от абсолютного нуля. С повышением температуры энтропия возрастает, так как движение частиц при этом становится более интенсивным и, следовательно, увеличивается беспорядок в системе. Энтропия возрастает при переходе вещества из кристаллического состояния в жидкое и из жидкого – в газообразное, при расширении газов, при химических взаимодействиях, приводящих к увеличению числа частиц, прежде всего, в газообразном состоянии.

Уравнение реакции позволяет судить о знаке изменения энтропии DS. Например, из уравнения:

NH₄NO_3(т) = N₂O_(г) + 2H₂O_(г)

следует, что из 1 моль твердого NH₄NO₃ образуется 3 моль газообразных веществ (1 моль N₂O_(г) и 2 моль H₂O_(г)). Следовательно, DS > 0.

Для расчета изменения энтропии в результате соответствующего процесса используют ее свойство функции состояния. Так, для реакции, протекающей по уравнению:

aA + bB = pP + qQ,

изменение энтропии будет равно:

DS°(298 К) = [pS°(P) + qS°(Q)] – [aS°(A) + bS°(B)]

(4.13).

Изменение энтропии в реакции образования 1 моль сложного вещества из простых веществ при стандартных условиях называется стандартной энтропией образования соединения и обозначается D_fS°(298 K). Для реакции

A + B = AB

в стандартных условиях значения абсолютной энтропии простых веществ

DfS°(298 K, AB) = S°(AB) – (S°(A) + S°(B))

(4.14).

4.5.4. НАПРАВЛЕНИЕ ХИМИЧЕСКИХ РЕАКЦИЙ В ИЗОЛИРОВАННЫХ СИСТЕМАХ. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ

В изолированных системах, т.е. в системах, которые не обмениваются с внешней средой ни веществом, ни энергией (ни теплотой, ни работой) и имеют поэтому постоянный запас внутренней энергии (U = const, DU = 0) и постоянный объем (A = p·DV = 0, то DV = 0) самопроизвольно идут только те процессы, которые сопровождаются ростом энтропии, DS > 0. При этом процесс может идти самопроизвольно до тех пор, пока энтропия не достигнет максимального для данных условий значения и тем самым равенства DS = 0. Рассмотренное положение представляет одну из формулировок второго закона термодинамики: изменение энтропии при самопроизвольном протекании химической реакции в изолированной системе всегда положительно.

Таким образом, рост энтропии является критерием термодинамической возможности самопроизвольного протекания химических реакций в изолированной системе, но изменение энтропии не является критерием направления и предела протекания реакций, при которых меняется внутренняя энергия системы, а также совершается работа против внешнего давления.

4.5.5. НАПРАВЛЕНИЕ ХИМИЧЕСКИХ РЕАКЦИЙ В НЕИЗОЛИРОВАННЫХ СИСТЕМАХ. ЭНТАЛЬПИЙНЫЙ И ЭНТРОПИЙНЫЙ ФАКТОРЫ ХИМИЧЕСКИХ РЕАКЦИЙ. ЭНЕРГИЯ ГИББСА

Как было показано выше, самопроизвольное протекание химических процессов сопровождается стремлением системы, с одной стороны, перейти в состояние с наименьшей энергией, т.е. выделить теплоту в окружающую среду - уменьшить энтальпию (стремление к порядку) и, с другой стороны, - в состояние с наибольшим беспорядком, т.е. увеличить энтропию (стремление к беспорядку). Поэтому, чтобы судить о возможности самопроизвольного протекания реакции, необходимо учитывать два фактора - энтальпийный (DH) и энтропийный (DS) (при p = const и T = const). Произведение T·DS дает энтропийному фактору размерность энергии, т.е. Дж/моль.

Общая движущая сила процесса	=	Энтальпийный (энергетический) фактор DH	– ­	Энтропийный фактор T·D S
		“противодействие”

Оба фактора определяют движущую силу химической реакции и для установления возможности ее самопроизвольного протекания должны оцениваться одновременно. Это осуществляется при помощи термодинамической функции состояния, которая называется энергией Гиббса (G):

G = H - T·S

(4.15).

Изменение энергии Гиббса представляет собой энергию, связанную с изменением энтальпии за вычетом энергии, необходимой для повышения неупорядоченности системы; другими словами речь идет об энергии, которая выделяется системой и может быть использована для совершения работы над ее окружением. Поскольку любая система самопроизвольно переходит в состояние с более низкой энергией, то процесс будет обладать способностью к самопроизвольному протеканию при условии, что знак DG < 0. Таким образом, при p = const и T = const самопроизвольно протекающие процессы идут в сторону уменьшения энергии Гиббса, поэтому условием (критерием) самопроизвольного протекания процесса при заданных T и p является неравенство D G < 0. Чем меньше D G, тем сильнее стремление к протеканию данного процесса и тем дальше он находится от состояния равновесия, при котором

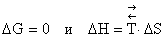(4.16).

где 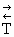- температура равновероятности протекания прямой и обратной реакций.

Если DG > 0, процесс самопроизвольно протекать не может. Критерием направления и предела самопроизвольного протекания процесса при V = const и T = const является разность

DA = DU - T·DS

(4.17).

Величина A называется энергией Гельмгольца и является функцией состояния.

4.5.6. РАСЧЕТ ВЕЛИЧИНЫ DG

Величину DG того или иного процесса в стандартных условиях можно рассчитать, используя ее свойство функции состояния. Для реакции, протекающей по уравнению:

aA + bB = pP + qQ

DG°(298 К) = [pDfG°(298 К, P) + qDfG°(298 К, Q)] – [aDfG°(298 К, A) + bDfG°(298 К, B)]

(4.18).

где D_fG°(298 К) – стандартная энергия Гиббса образования сложного вещества. Под стандартной энергией Гиббса образования D_fG°(298 К) понимают изменение энергии Гиббса в реакции образования 1 моль сложного вещества из простых веществ в стандартных условиях (T = 298,15 K, p = 101,3 кПа). Для простых веществ, устойчивых в стандартных условиях, D_fG°(298 К) = 0. Для многих веществ величины D_fG°(298 К) являются справочными.

Изменения стандартной энергии Гиббса D_fG°(298 К) в реакции может быть рассчитано также по уравнению (4.15):

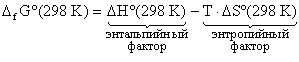
если известны изменения стандартных энтальпии и энтропии химической реакции, а также температура.

4.5.7. ЭНЕРГИЯ ГИББСА И ТЕМПЕРАТУРА

В уравнении DG = DH - T·DS величины DH и -T· DS имеют противоположные знаки, и от их относительной величины зависит, будет ли значение DG отрицательным или положительным. В этих случаях важно учитывать температуру процесса. При низких температурах доминирует вклад энергетического фактора: |DH| >> |-T·DS|, а при высоких температурах - вклад энтропийного фактора: |-T·DS| >> |DH|. Энтропийный вклад, определяемый величиной "-T·DS", может повысить или, наоборот, понизить способность реакции к самопроизвольному протеканию. При DS > 0 член "-T·DS" вносит отрицательный вклад в величину DG, т.е. повышает тенденцию реакции к самопроизвольному протеканию. При DS < 0 член "-T·DS", наоборот, уменьшает тенденцию реакции к самопроизвольному протеканию.

Из уравнения (4.15) видно, что изменение энергии Гиббса будет отрицательным (DG < 0), то есть процесс будет протекать самопроизвольно:

1. при любой температуре, если DH < 0 и DS > 0;
2. при высокой температуре, если DH > 0 и DS > 0;
3. при низкой температуре, если DH < 0 и DS < 0.

Если DH > 0, а DS < 0, то DG > 0 при любых температурах, а реакция является не самопроизвольной (самопроизвольной будет обратная реакция).

На рисунке 4.5 приведены графические зависимости изменения энергии Гиббса химических реакций от температуры. Видно, что при одинаковом знаке величин DH и DS (либо DH > 0 и DS > 0, либо DH < 0 и DS < 0) возможно изменение знака DG. В случае с разноименными знаками величин DH и DS (и частных случаев DH = 0 или DS = 0) изменение знака величины DG не происходит. Поэтому для реакции с одноименными по знаку величинами DH и DS можно вычислить температуру равновероятности 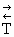, выше (для DH < 0 и DS < 0) или ниже (DH >0 и DS > 0) которой данная реакция в прямом направлении становится термодинамически менее вероятной в стандартных условиях. Вычисленное значение 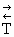может оказаться реально недостижимым, если вещества, участвующие в реакции, начнут вступать в побочные реакции или менять свое агрегатное состояние.

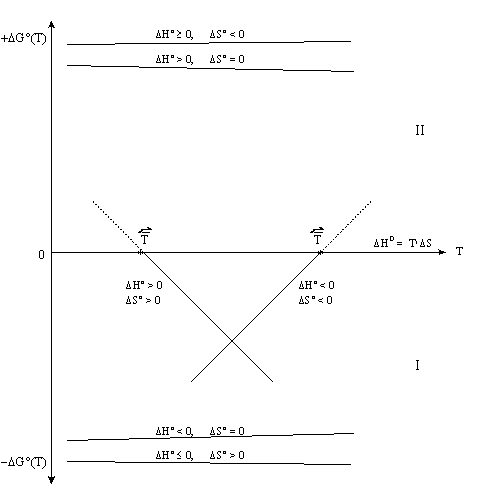
Рис. 4. 5. Зависимость стандартной энергии Гиббса реакции DG°(Т) от температуры T: I - область преобладания прямых реакций; II - область преобладания обратных реакций.

При пользовании значениями стандартной энергии Гиббса критерием принципиальной возможности процесса в нестандартных условиях следует принять условие DG° << 0, а критерием принципиальной невозможности осуществления процесса неравенство DG° >>