Параграф 11. закон гюи-стодолы.

Эксергия есть максимальная работа, которая совершается при обратимом переходе системы в равновесие с окружающей средой. Наличие необратимости приводит к уменьшению работы, т. е. потере части эксергии. Рассмотрим теплосиловую установку, которая представляет собой открытую систему (рисунок 11.1). В установку вводится рабочее тело с параметрами H₁, S₁ и теплота Q₁ от источника теплоты с температурой Т. Из установки рабочее тело выходит с параметрами Н₂ и S₂. Теплота 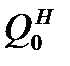от установки отводится в окружающую среду с температурой Т₀. Полезная работа для этой термодинамической системы будет определяться как

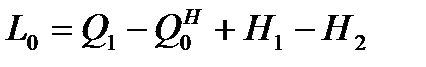. (11.1)

Для сравнению возьмем установку, в которой при тех же параметрах рабочего тела на входе и выходе все процессы протекают обратимо. Вследствие обратимости совершаемая работа станет максимально возможной

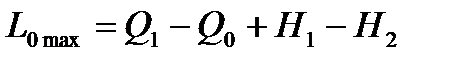, (11.2)

где Q₀ ‒ теплота, отводимая в окружающую среду при обратимом течении процессов в установке.

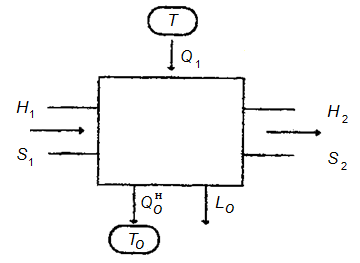
Рисунок 11.1 ‒ Схема потоков вещества и энергии в

теплосиловой установке

Тогда потери работоспособности, вызванные необратимостью, составят

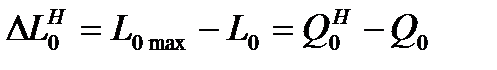. (11.3)

При этом следует учитывать, что при отводе теплоты 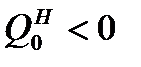и .

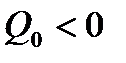Суммарные приращения энтропии рабочего тела и окружающей среды при необратимом и обратимом протекании процессов в установке будут соответственно равны

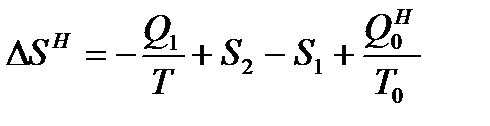, (11.4)

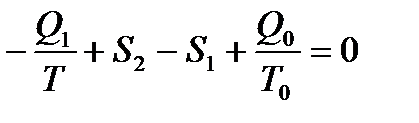. (11.5)

Вычитая (11.5) из (11.4), получим выражение для потерь работоспособности вследствие необратимости

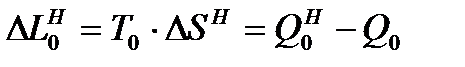. (11.6)

Покажем, что формула (11.6) является универсальной и выражает потери работоспособности или эксергии вследствие любого вида необратимости. Рассмотрим работу ХТС в стационарном, установившемся режиме. Давление в системе не меняется, т. е. работа не совершается (рисунок 11.2). На вход системы подаются потоки эксергии, из системы с уходящими потоками эксергия уходит из ХТС.

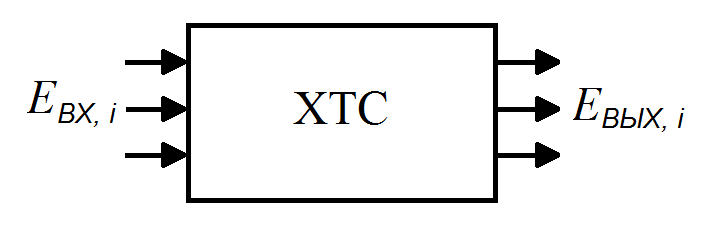
Рисунок 11.2 ‒ К выводу закона Гюи-Стодолы

В соответствии с первым законом термодинамики в любом процессе 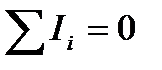. В обратимом процессе 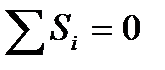. Следовательно, в этом случае эксергия не теряется, т. е. 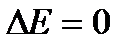. В реальной процессе .

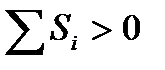Исходя из современных представлений физического смысла понятия эксергии, суммарная эксергия потоков на входе в ХТС

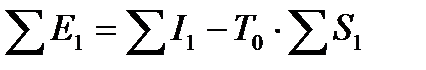, (11.7)

на выходе из ХТС

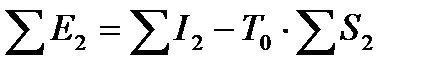, (11.8)

а изменение эксергии в ходе протекающих в ХТС процессов равно

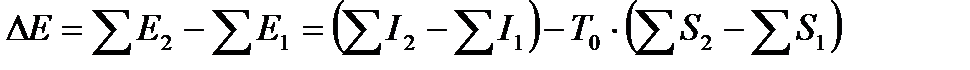. (11.9)

Поскольку всегда 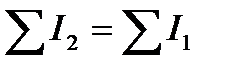, то

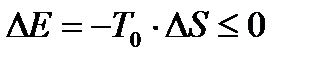. (11.10)

Это уравнение, показывающее, что эксергия убывает пропорционально энтропии, называется законом Гюи-Стодолы. Оно показывает, какое количество работы безвозвратно теряется вследствие нерационального аппаратурно-технологического оформления процесса или из-за принципиальных его особенностей, приводящих к термодинамической необратимости.

Закон Гюи-Стодолы позволяет вычислить потери эксергии как в любых ХТС в целом, так и в отдельных ее элементах. В последнем случае общие потери получаются путем суммированием потерь в элементах.