Условие равновесия фаз в гетерогенной системе

Изменения энергии Гельмгольца F и энергии Гиббса G раствора зависят от масс компонентов составляющих раствор:

dF = - PdV – SdT + Σμ_idn_i (7.22)

dG = VdP – SdT + Σμ_idn_i, (7.23)

где Σμ_idn_i – член уравнения, учитывающий изменение величин F и G в

зависимости от изменения масс компонентов раствора;

μ_i – химический потенциал i – го компонента раствора.

Если V = Const и T = Const, то из уравнения (7.22) следует:

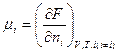(7.24)

Если P = Const и T = Const, то из уравнения (7.23) следует:

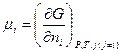(7.25)

Величины химического потенциала, выраженные в уравнениях (7.24) и (7.25) равны между собой:

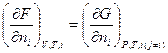= μ_i (7.26)

Для термодинамической теории растворов особенно важное значение имеет уравнение химического потенциала, выраженного через энергию Гиббса. Из уравнения (7.25) видно, что химический потенциал компонента раствора представляет собой парциальную молярную энергию Гиббса компонента.

μ_i = 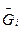(7.27)

Таким образом, химическим потенциалом какого либо компонента раствора называется приращение энергии Гиббса при добавлении к большому количеству раствора, находящемуся при постоянных Р и Т, одного моля данного компонента.

Химический потенциал может служить критерием равновесия в гетерогенной системе. Рассмотрим гетерогенную систему, состоящую из фазы 1 и фазы 2. Пусть каждая из этих фаз представляет собой раствор, в котором имеется компонент i. Если фазы находятся в равновесии друг с другом, то для условий равновесия справедливо:

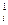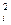μ = μ (7.28)

Справедливо и обратное утверждение: если химический потенциал компонента в одной фазе равен химическому потенциалу этого компонента в другой фазе, то фазы находятся в равновесии друг с другом.

Это правило распространяется на любую гетерогенную систему, состоящую более чем из двух фаз.

Растворы идеальных газов

Газовая смесь называется идеальным раствором, если каждый её компонент подчиняется уравнению Менделеева – Клапейрона. Для каждого компонента такой смеси можно записать:

d 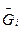= VdP_i - Td 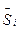(7.29)

Для условия Т = Const уравнение (7.29) примет вид:

d 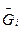= VdP_i (7.30)

С учётом того, что газ является идеальным, можно записать для одного моля газа:

V = 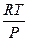(7.31)

Тогда уравнение (7.30) примет вид:

d 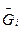= 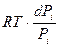(7.32)

Проинтегрируем уравнение (7.32) в пределах стандартное состояние, которому отвечает 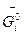, и данное состояние, которому отвечает :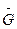

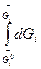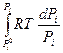= (7.33)

или

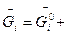
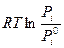, (7.34)

где P 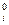- давление газа i в стандартном состоянии.

Для нормальных условий давление газа в стандартном состоянии равно

одной атмосфере. Тогда из уравнения (7.34) получим:

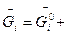
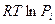(7.35)

Из определения химического потенциала компонента следует, что μ_i = 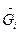. Тогда получим для химического потенциала компонента идеальной газовой смеси при постоянной температуре:

μ_i = μ 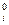+ RTlnP_i, (7.36)

где μ 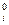- стандартный химический потенциал i – го компонента идеальной

газовой смеси, величина которого зависит только от температуры.

Рассуждая аналогичным образом, можно получить уравнения для химического потенциала компонента идеальной газовой смеси, выраженные через другие концентрации компонента:

μ_i = μ 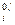+ RTlnС_i (7.37)

и

μ_i = μ 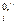+ RTlnХ_i, (7.38)

где С_i – молярная концентрация i – го компонента смеси;

Х_i - концентрация i – го компонента смеси, выраженная в молярных

долях.

Поскольку химический потенциал компонента представляет собой парциальную молярную энергию Гиббса, то для газовой смеси , состоящей из n₁ молей компонента 1 и n₂ молей компонента 2, справедливо уравнение Гиббса – Дюгема:

n₁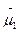d + n₂d 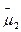= 0 (7.39)

Дифференцирование уравнение химического потенциала при Т = Сonst даёт:

dμ_i = RTlnP_i (7.40)

После подстановки уравнения (7.40) в уравнение (7.39) получим:

n₁dlnP₁ + n₂dlnP₂ = 0 (7.41)

или для одного моля раствора

Х₁dlnP₁ + Х₂dlnP₂ = 0 (7.42)

Уравнения (7.41) и (7.42) называют уравнениями Гиббса – Дюгема – Маргулеса.