Статистическая проверка гипотез

МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ЭКСПЕРИМЕНТА

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Эксперимент — система операций и (или) наблюдений, направленных на получение информации об объекте исследования. Составной частью экспе­римента является опыт — воспроизведение исследуемого явления в опреде­ленных условиях при возможности регистрации и количественной оценки со­стояния или результатов функционирования исследуемого объекта. Экспери­мент проводится на промышленном оборудовании, лабораторной установке или физической модели. При этом механизм изучаемого процесса обычно известен лишь частично или совсем неизвестен. В таких случаях объект исследования можно условно представить в виде «черного ящика» — системы внутренних связей, не доступных исследователю. Известны лишь переменные величины, воздействующие на объект исследования, и величины, характеризующие его состояние или результаты функционирования (рис. 3.1). Первые называют входными величинами или факторами, а вторые — выходными или откликом.

Все факторы делятся на три группы:

1) группа постоянных или случайно изменяющихся в ходе исследования факторов W, значения которых известны;

2) группа управляемых факторов U, значения которых выбираются и це­ленаправленно изменяются в ходе исследования (две первых группы часто объединяют в одну группу контролируемых факторов X);

3) группа неконтролируемых факторов Z, значения которых остаются по той или иной причине неизвестными в ходе исследования.

Изменение отклика У под действием монотонно изменяющихся во време­ни неконтролируемых факторов называется временным дрейфом отклика, а за­висимость математического ожидания отклика от контролируемых факторов — функцией отклика.

Геометрическое представление функции отклика называет­ся поверхностью отклика. Чтобы такое представление стало возможным, вво­дится понятие факторного пространства, у которого координатные оси соответствуют отдельным факторам. Пример трехмерного факторного пространства показан на рис. 3.2.

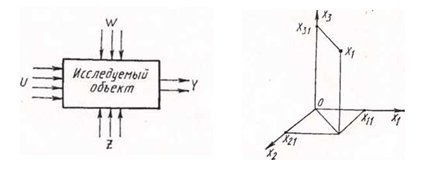
Рис. 3.1. Кибернетическая модель объекта исследования

Рис. 3.2. Геометрическая мо­дель трехфакторного простран­ства

Любая точка факторного пространства характеризуется набором значений факторов, при которых производится измерение отклика. Фиксированное зна­чение фактора называют также уровнем фактора. При количестве факторов, большем трех, геометрическое моделирование факторного пространства ста­новится невозможным. Поэтому чаще всего множество уровней факторов, при которых производится измерение отклика, задается матрицей условий экспе­римента. Эта матрица для k факторов и N измерений имеет вид

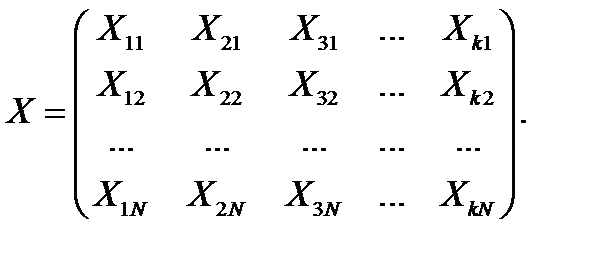
Значения отклика, полученные при данных измерениях, также представ­ляются в матрице, которая имеет один столбец и называется матрицей наблю­дений:

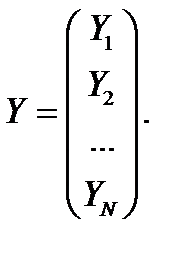(3.1)

По характеру организации и методам обработки результатов эксперимент может быть пассивным или активным.

При реализации пассивного эксперимента исследователь наблюдает за объектом, не вмешиваясь в процесс его функционирования. Поскольку в дан­ном случае уровни факторов случайным или закономерным образом изменя­ются во времени, то появляется возможность, измеряя их значения и значения отклика, исследовать зависимость между факторами и откликом. Примером пассивного эксперимента является исследование точности обработки деталей на настроенном станке. Факторами в данном случае будут погрешности загото­вок, их твердость, износ инструмента, жесткость станка, откликом — погреш­ность обработанных деталей.

При реализации активного эксперимента исследователь сам изменяет уро­вень факторов и поддерживает их на нужном уровне в течение данного этапа эксперимента.

К контролируемым факторам предъявляются следующие требования, ко­торые должны учитываться при подготовке активного эксперимента.

1. Управляемость фактора — возможность поддерживать выбранный уро­вень фактора в течение необходимого для измерения отрезка времени.

2. Достаточно высокая точность, с которой поддерживается и измеряет­ся уровень фактора.

3. Независимость фактора — возможность задать любой уровень данного фактора вне зависимости от уровней других факторов.

4. Совместимость факторов — безопасность функционирования объекта исследования и возможность измерения отклика в любой точке той части фак­торного пространства, которая является областью экспериментирования.

Кроме факторов, каждому уровню которых после измерения можно по­ставить в соответствие определенное число, могут быть и качественные фак­торы (например, рецепты связок шлифовальных кругов, материалы режущей части инструмента, химический состав обрабатываемого материала). В этом случае каждому уровню качественного фактора нужно поставить в соответ­ствие число натурального ряда (код). Порядок уровней качественных факто­ров может быть произвольным, но после кодирования он фиксируется. Для упрощения расчетов при обработке результатов эксперимента рекомендуется проводить нормализацию факторов — преобразование их в безразмерные ве­личины с (по возможности) целочисленными значениями. При симметричной нормализации расчетная формула имеет вид

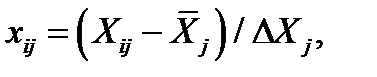(3.2)

где x_ij — нормализованный i-й уровень j-го фактора; Х_ij — натуральный i-й уровень j-го фактора; ΔX_j — постоянный шаг изменения натурального значе­ния j-го фактора; X_j — средний уровень j-го фактора:

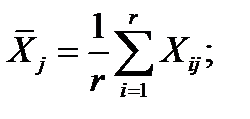(3.3)

r — число уровней фактора.

Чтобы нормализованные факторы приняли целочисленные значения, чис­ло уровней их должно быть нечетным. Например, при r = 5 коды факторов при­нимают значения -2; -1; 0; 1; 2.

При несимметричной нормализации

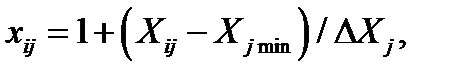(3.4)

где X_{j min} — минимальный уровень j-го фактора.

В данном случае нормализованные факторы принимают значения 1, 2, 3, ..., r. В качестве факторов могут приниматься не только физические или гео­метрические величины, но и некоторые функции от них (например, логарифмы или показательные функции).

При выборе отклика из нескольких, обычно функционально связанных показателей результата функционирования исследуемого объекта должно учи­тываться следующее.

1. Необходимо, чтобы отклик был однозначным в статистическом смысле, т. е. заданному набору уровней факторов должно соответствовать одно (с точ­ностью до погрешности измерения) значение отклика.

2. Отклик должен быть эффективным в статистическом смысле. Это зна­чит, что из нескольких функционально связанных откликов выбранный можно измерить с наибольшей точностью.

3. Желательно, чтобы отклик можно было оценить количественно. Если нет способа количественного измерения результата, то следует пользоваться ранжированием. При этом отклику присваиваются оценки — ранги по заранее выбранной шкале.

План эксперимента — совокупность данных, определяющих число, условия и порядок реализации опытов. План эксперимента обычно записыва­ется в виде матрицы плана — прямоугольной таблицы, строки которой отве­чают отдельным опытам, а столбцы — факторам. Элементами матрицы плана обычно являются нормированные уровни факторов, т.е. (и, j)-й элемент равен нормированному уровню j-го фактора в u-м опыте. Матрица плана может иметь совпадающие строки. Чтобы сократить запись, используется матрица спектра плана, составленная из всех строк матрицы плана, отличающихся уровнем хо­тя бы одного фактора, и матрица дублирования — квадратная диагональная матрица, элементы которой равны числам параллельных (дублирующих) опы­тов в соответствующих точках спектра плана.

План, содержащий все возможные комбинации всех факторов на опреде­ленном числе уровней равное число раз, называется полным факторным пла­ном. Если план содержит только часть комбинаций полного факторного пла­на, то его называют дробным факторным планом или дробной репликой пол­ного факторного плана.

СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ

Основные определения

Статистическая гипотеза — предположение относительно статистических параметров генеральной совокупности или закона распределения случайных величин, проверяемое на основе выборочных данных.

Основная проверяемая гипотеза (нулевая гипотеза) обычно обозначается Н₀. Одновременно формулируется альтернативная или конкурирующая гипоте­за Н₁. Например, если проверяется равенство математического ожидания ге­неральной совокупности некоторому значению μ₀, нулевая гипотеза Н₀ – М(Y) = μ₀, альтернативная гипотеза Н₁ – М(Y) ≠ μ₀.

Критерием статистической гипотезы называют правило, позволяющее при­нять или отвергнуть гипотезу на основании выборки из генеральной совокуп­ности. Принимая или отклоняя гипотезу Н₀, можно допустить ошибки двух видов. Ошибка первого рода состоит в том, что гипотеза Н₀ отвергается, в то время как в действительности она верна, ошибка второго рода – гипотеза Н₀ принимается, в то время как верна гипотеза H₁.

Вероятность ошибки первого рода обозначается α. Ее часто называют уровнем значимости критерия гипотезы. Вероятность ошибки второго рода обо­значается β. Вероятность 1 – β принятия гипотезы Н₁, когда она верна, назы­вается мощностью критерия гипотезы Н₀ относительно альтернативной гипо­тезы Н₁. Очевидно, что при проверке гипотезы Н₀ относительно альтернатив­ной гипотезы Н₁ лучшим является тот критерий, который обеспечивает наиболь­шую мощность при том же самом уровне значимости α.