Спектральные закономерности

Опыт 12.1«Столкновение частиц»

Оборудование:

1. микроскоп (с увеличением 50 )

2. предметное стекло

3. покровное стекло (толщиной 0,18 мм)

4. акварельные краски

5. кисточка

6. стеклянная палочка

7. фильтровальная бумага

8. порошкообразное вещество

Ход работы:

На предметное стекло при помощи стеклянной палочки нанесите каплю воды. Небольшое количество краски кисточкой добавьте в воду (вода должна лишь слегка окраситься). Поверх капли положите покровное стекло. При необходимости наклоном предметного стекла удалите из взвеси возникшие пузырьки воздуха. Под покровным стеклом должно находится такое количество воды, чтобы при любом наклоне предметного стекла покровное стекло не смещалось. Излишнюю воду нужно удалить при помощи полоски фильтрованной бумаги, подносимой к краю покровного стекла. Эксперимент будет тем удачнее, чем тоньше слой воды между стеклами.

Готовый препарат помещается на столик микроскопа. При приближении объектива к препарату сначала видны лишь крупные частицы туши. Эти частицы не проявляют броуновского движения. Вблизи крупных частиц видны более мелкие, вот они и находятся в непрерывном движении (или «дрожании»), получая различные импульсы от молекул воды.

Выводы: При выполнении опыта демонстрируется броуновское движение частиц.

Опыт 12.2 Регистрация заряженных частиц с помощью камеры Вильсона

Оборудование:

Камера Вильсона – трековый детектор элементарных заряженных частиц, в котором трек (след) частицы образует цепочка мелких капелек жидкости вдоль траектории её движения. Изобретена Ч. Вильсоном в 1912 г. (Нобелевская премия 1927 г.).

Ход работы:

Принцип работы камеры Вильсона основан на конденсации пересыщенного пара и образовании видимых капель жидкости на ионах вдоль следа пролетевшей через камеру заряженной частицы. Для создания пересыщенного пара происходит быстрое адиабатическое расширение газа с помощью механического поршня. После фотографирования трека, газ в камере снова сжимается, капельки на ионах испаряются. Электрическое поле в камере служит для “очистки” камеры от ионов образовавшихся при предыдущей ионизации газа. В камере Вильсона треки заряженных частиц становятся видимыми благодаря конденсации перенасыщенного пара на ионах газа, образованных заряженной частицей. На ионах образуются капли жидкости, которые вырастают до размеров достаточных для наблюдения (10–3-10–4 см) и фотографирования при хорошем освещении. Рабочей средой чаще всего является смесь паров воды и спирта под давлением 0.1-2 атмосферы (водяной пар конденсируется главным образом на отрицательных ионах, пары спирта – на положительных). Перенасыщение достигается быстрым уменьшением давления за счёт расширения рабочего объёма. Возможности камеры Вильсона значительно возрастают при помещении её в магнитное поле. По искривлённой магнитным полем траектории заряженной частицы определяют знак её заряда и импульс. С помощью камеры Вильсона в 1932 г. К. Андерсон обнаружил в космических лучах позитрон.

Вывод: В ходе опыта демонстрируется принцип работы камеры Вильсона.

Опыт 12.3 Регистрация заряженных частиц с помощью счетчика Гейгера

Оборудование:

Счётчик Гейгера представляет собой, как правило, цилиндрический катод, вдоль оси, которого натянута проволока — анод. Система заполнена газовой смесью.

Ход работы:

При прохождении через счётчик заряженная частица ионизирует газ. Образующиеся электроны, двигаясь к положительному электроду — нити, попадая в область сильного электрического поля, ускоряются и в свою очередь ионизуют молекулы газа, что приводит к коронному разряду. Амплитуда сигнала достигает нескольких вольт и легко регистрируется.

Вывод: При выполнении работы мы убедились в том, что счётчик Гейгера регистрирует факт прохождения частицы через счётчик, но не позволяет измерить энергию частицы.

1. Накаленные твердые тела испускают сплошные спектры. У газов (наряду со сплошной областью) наблюдаются линейчатые и полосатые спектры. Линейчатый спектр состоит из ряда закономерно расположенных более или менее узких спектральных линий. В полосатом спектре полосы кажутся сплошными при наблюдении в спектроскоп малой разрешающей силы. При применении спектрального аппарата высокой разрешающей силы они распадаются на множество тесно расположенных спектральных линий.

К началу ХХ-го века было выяснено, что линейчатые спектры газов испускаются атомами и ионами, а полосатые — молекулами. Поэтому их называют также атомными и молекулярными спектрами. Атомный спектр водорода удается наблюдать при электрическом разряде в вакуумной водородной трубке только тогда, когда большая часть молекул водорода диссоциировала на атомы. Но в парах йода полосы молекулярного спектра в основном исчезают уже в процессе диссоциации молекул I₂ на атомы I. Наличие многих спектральных линий атома указывает на сложность его внутренней структуры. Неудивительно, что богатейший материал, накопленный эмпирически при изучении спектров, послужил в ХХ-м веке основным фундаментом, на котором развилась теория строения атома. Положение спектральной линии в спектре характеризуется длиной
волны λ или частотой 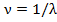. Частота более удобна для выражения спектральных закономерностей. Но для ее вычисления надо знать скорость света с, а она была измерена с недостаточной точностью, во всяком случае до самого последнего времени. Длина же волны λ измеряется спектральным аппаратом с высокой точностью — до седьмого десятичного знака и выше. Поэтому вместо 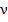спектроскописты употребляют так называемое спектроскопическое волновое число 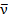. Это есть число волн, укладывающихся в вакууме на 1 см длины:

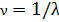(12.1)

(В настоящее время приведенные соображения утратили свое значение. Методами нелинейной оптики удалось на опыте измерить частоту световых колебаний и притом с точностью, превышающей измерение длины волны в спектроскопии. Скорость же света в вакууме связана с частотой 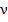и длиной волны λ соотношением с=λ 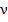. Поэтому в октябре 1983 г. Генеральная конференция по мерам и весам приняла новое определение метра. По этому определению скорость света в вакууме принимается равной с=2,99792458 × 10⁸ м/с точно. Метр же определяется через расстояние, проходимое светом в вакууме в течение одной секунды- Поэтому в принципе было бы безразлично, пользоваться ли в сектроскопии величиной 1/λ или величиной c/λ. В спектроскопии частоту и спектроскопическое волновое число принято обозначать одной и той же буквой 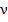. Во избежание недоразумений мы этого делать не будем. Частоту будем обозначать через 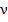, а спектроскопическое волновое число — через 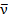, т. е. в последнем случае ставить над 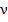черточку. Впрочем, вместо 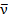предпочтительнее пользоваться обозначением 1/λ.

2. Основным законом спектроскопии, установленным эмпирически в 1908 г., является комбинационный принцип Ритца. Он состоит в том что вое многообразие спектральных линий рассматриваемого атома может быть получено путем попарных комбинаций гораздо меньшего числа величин, называемых спектральными термами или сокращенно просто термами. Частота (волновое число) каждой спектральной линии выражается разностью двух термов:

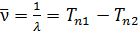(12.2).

Термы принято считать существенно положительными и нумеровать их так, чтобы с возрастанием номера терма его величина уменьшалась. В приведенной формуле, например, должно быть n₁ < n₂; T_n1 > T_n2. Если фиксировать n₁ и придавать n₂ всевозможные возрастающие значения, начиная с n₂ =n₁ + 1, то получится система линий, называемая спектральной серией. Совокупность спектральных серий составляет спектр рассматриваемого элемента (атома).
Рассмотрим две спектральные линии одной и той же серии:

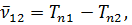
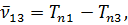
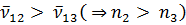
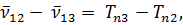
последнее равенство получено вычитанием из первого равенства второго.
Но это есть волновое число какой-то спектральной линии того же элемента, принадлежащей к серии с начальным термом Т_n3. Таким образом, из комбинационного принципа следует, что разность частот (волновых чисел) двух спектральных линий одной и той же серии атома дает частоту (волновое число) спектральной линии какой-то другой серии того же атома. Впрочем, такой линии может не оказаться в спектре, так как на комбинации термов друг с другом накладываются некоторые ограничения, называемые правилами отбора.

Аналитические выражения для термов подавляющего большинства элементов неизвестны. В лучшем случае они представляются приближенными эмпирическими или полуэмпирическими формулами. Исключение составляет простейший атом — атом водорода, состоящий из одного протона и одного электрона. Для атома водорода терм с высокой степенью точности имеет вид

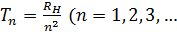), (12.3)
где R_H — постоянная, называемая постоянной Ридберга (1854-1919) для водорода. Ее числовое значение равно
R_H= 109678,76(1) см^-1 (12.4).

Такое же выражение, но с другим числовым значением постоянной Ридберга справедливо для всех изотопов водорода и всех одноэлектронных ионов.

Из выражения (12.3) путем комбинаций получаются следующие спектральные серии: Серия Лаймана:

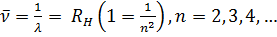(12.5).

Эта серия была открыта Лайманом (1874-1954) в 1916 г. в ультрафиолетовой области спектра. Серия Бальмера:

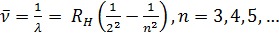(12.6).

Четыре первые линии этой серии лежат в видимой области спектра и обозначаются через Н_α, H_β, Н_γ, Н_δ, остальные — в области ультрафиолета. На этих четырех линиях Бальмером (1825-1898) в 1885 г. и была выявлена закономерность, выражаемая формулой (12.6). С этого началось систематическое исследование спектральных серий. Мы приводим схематическое изображение серии Бальмера (рис. 12.1).

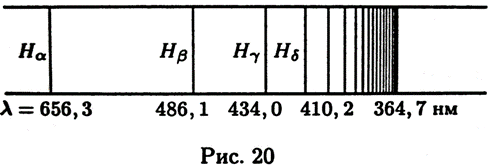
Рисунок 12. 1

Таблица 2, в которой приведены вычисленные и наблюденные значения длин волн для первых девяти линий серии Бальмера, показывает, с какой не высокой точностью формула (12.6) согласуется с опытом. Длины волн отнесены к воздуху, где они были экспериментально измерены. Поэтому вычисленные по формуле (12.6) длины волн были пересчитаны для воздуха.

Таблица. Длины волн бальмеровской серии водорода

n	Обозначение	λ, нм
вычисление	наблюдение
	Hα	656,279	656,285
	Hβ	486,133	486,132
	Hγ	434,047	434,046
	Hδ	410,174	410,173
	Hε	397,008	397,007
	Hζ	388,905	388,906
	Hη	383,539	383,540
	Hθ	379,790	379,791
	H	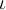377,067	377,065

Таблица 12. 1

Серия Пашена:

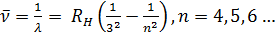(12.7).

Эту серию предсказал Ритц в 1908 г. на основе комбинационного принципа. Все линии этой серии получаются путем комбинаций из линий серии Бальмера. Рассматриваемая серия в том же году была обнаружена Пашеном (1865-1947) в инфракрасной области спектра.

Серия Брэккета:

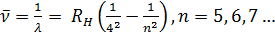(12.8).

Серия Пфунда:

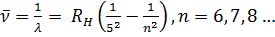(12.9).

Эти серии лежат в далекой инфракрасной области спектра. Они были открыты в 1922г. и 1924г. соответственно. Конечно, серия Брэккета получается путем комбинаций из линий серии Пашена, а серия Пфунда (1879-1949) — из линий серии Брэккета.
Максимальная длина волны для серии Лаймана получается при n=2. Она равна λ=4/3R_H=121,56713 нм. Соответствующая линия называется резонансной линией водорода. Максимальная частота (волновое число) получится по формулам (12.5)—(12.9) при n равном бесконечности. Эта частота называется границей серии. Для серии Бальмера, например, граница серии равна

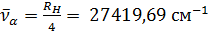или 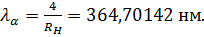(12.8).
При приближении к границе серии спектральные линии сгущаются -разность длин волн между ними асимптотически стремится к нулю: стремятся к нулю и интенсивности линий. За границей серии спектр не обрывается, а становится сплошным. Эта закономерность проявляется в спектральных сериях не только водорода, но и других элементов. Здесь также существуют границы серий, за которыми следует сплошной спектр.