Уравнение плоской волны, не затухающей с расстоянием, в комплексной форме имеет вид

U=u_me^j(wt-kr)

здесь u_m = u_m^jфu – комплексная амплитуда; r – радиус-вектор рассматриваемой точки; k –волновой вектор, численно равный волновому числу

k=w/c=2π/λ

где с λ – соответственно скорость распространения и длина волны.

Распространение волны всегда связано с переносом энергии, которая количественно характеризуется мгновенным вектором плотности потока энергииIt. На практике обычно пользуются понятием интенсивности волны I, которая равна модулю среднего значения вектораItза время, равное периоду T полного колебания. Найдем интенсивности звука и электромагнитной волны. Для этого введем понятие импеданса среды при распространении волны.

Комплексным импедансом среды при распространении звуковой волны назовем отношение

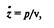
где р и v – соответственно звуковое давление и колебательная скорость.

Комплексным импедансом среды при распространении электромагнитной волны назовем отношение поперечных составляющих электрического (Е) и магнитного (Н) полей в данной точке:

z=E/H

Положив u=p для звука и u=E для электромагнитного поля, можно для определения интенсивности звуковой волны или для определения интенсивности электромагнитной волны использовать одну и ту же формулу*:

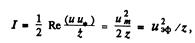
i-^^-^-^^ ^w

Эффективное значение величины u

где

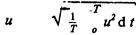
При заданных стандартом референтных значениях. I*U*Z* удовлетворяющих условию I* = U*/Z* из соотношения (6.25) следует

L_I=L_U+L_Z

**Числовые значения референтных величин различны для звука и ЭМП.

L_I=101gI/I*, *(6.26)–

где L_U=201gu_эф/Г*Г; L_Z=101gz/z* уровни величин I,U,Z. Суммарная интенсивность некогерентных источников

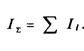
Следовательно, уровень суммарной интенсивности

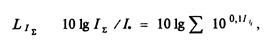
где Lit, и п – соответственно уровень интенсивности i-го источника и число источников. Если все п источников имеют одинаковый уровень интенсивности, равный Lt, то уровень суммарной интенсивности будет равен

L_IE=L_I+101gn

Источники направленного действия характеризуют коэффициентом направленности, равным отношению:

Ф=I/I_H

где I–интенсивность волны в данном направлении на некотором расстоянии r от источника направленного действия мощностью W, излучающего волновое поле в телесный угол Ω; Iн= W/(4πr²) –интенсивность волны на том ж е расстоянии при замене данного источника на источник ненаправленного действия той же мощности. В общем случае в сферической системе координат, характеризуемой углами ø и φ, коэффициент направленности φ= φ(ø). Для осесимметричных источников коэффициент направленности не зависит от координаты ф и ф=ф(ø). Таким образом, интенсивность можно выразить через мощность источника следующим образом:

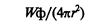
При необходимости учесть затухание в уравнение (6.23) вводят вместо волнового числа k комплексное волновое число fc, или коэффициент распространения k:

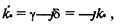
где γ и δ – соответственно коэффициент фазы и коэффициент затухания. Амплитуда затухающей волны будет равна um(δ) = u_meδr a интенсивность волны будет затухать по закону:

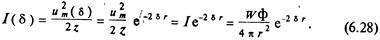
На расстоянии r затухание в децибеллах

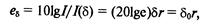
где δо = 8,686δ – коэффициент затухания, выраженный в децибелах на единицу длины.

Полагая Wx =I*Seиз выражения (6.28) находим уровень интенсивности с учетом затухания:

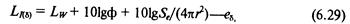
где Se и Lw=101gW/W* –соответственно единичная площадь и уровень мощности относительно референтного значения W*:

Таким образом, уровень интенсивности в данной точке определяется через уровень мощности и коэффициент направленности. Формула (6.29) справедлива в свободном волновом поле, т. е. поле, не имеющем границ, от которых могло бы происходить отражение волн. Свободное поле можно создать и в помещении, если сделать последнее из материала, полностью поглощающего энергию падающей волны. Величину 101gф называют показателем направленности и обозначают ПН.

Таблица 6.7. Коэффициент затухания звука в воздухе, дБ/км

Относительная влажность возду-	Среднегеометрические частоты октавных полос, Гц
ха,%
	0.8	1,5	3,8	12,1
	0,4	1,3	2,8	4,9
	0,2	0,9	2,7	5,5	9,7

Для звука коэффициент затухания δо зависит от частоты звука, температуры, давления и относительной влажности воздуха. При нормальном атмосферном давлении и температуре воздуха, равной +20 °С , значения коэффициента δо даны в табл. 6.7. Для электромагнитной волны, распространяющейся в воздухе, δо≈0 (см. ниже). Следует иметь в виду, что в реальных условиях уровень затухания зависит также от погодных условий (дождь, снег, туман и т. д.), наличия растительности (трава, кустарник, деревья и т. д.), состояния атмосферы (ветер, туман, турбулентность, температурные градиенты и т. д.), наличия отражающих поверхностей (земля, преграды, экраны и т. д.) и ряда других факторов и вычисляется по формуле где eS(i) – уровень

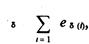
затухания при наличии i-го фактора. Если затуханием можно пренебречь (S = 0), то уровень интенсивности:

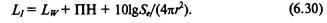
Диффузное волновое поле в изолированных объемах. Волновое поле называют диффузным, если усредненная по времени объемная плотность энергии W=Wg одинакова во всех точках, а поток энергии через единичную площадку в любой точке и в любом направлении постоянен и равен 1g

Энергия волны в объеме d V равна ck=WgdK В диффузном поле эта энергия распределяется равномерно во все стороны пространства 4я. Следовстгельно, на телесный угол dQ = d5fcos6/r² приходится часть энергии, равная d^ == w^cosOd V(\S/^nr¹. В сферической системе координат с полярным углом 9 элементарный объем d^=" AinOdOdcpdr и полная энергия через площадку d*? найдется в результате следующего интегрирования:

Откуда следует, что поток энергии через единичную площадку

Ig=Wgc/4=Iв/4

Таким образом, поток энергии через единичную площадку в диффузном волновом поле в четыре раза меньше интенсивности Iв бегущих волн с той же объемной плотностью энергии. Для бегущей со скоростью с волны интенсивность I = cw, где w – усредненная объемная плотность энергии. При наличии диффузного поля понятие интенсивности теряет смысл.

Понятие диффузного поля часто используют при определении плотности потока энергии Iп в изолированных объемах. Под изолированным объемом понимается пространство, огражденное стенками (например, производственное помещение, кабина, пространство под кожухом машины и т. д.). Волны в изолированных объемах, многократно отражаясь, образуют поле, которое изменяется при изменении геометрических размеров, формы и других характеристик источника.

Волновое поле в каждой точке изолированного объема можно представить в виде совокупности волн, непосредственно приходящих в эту точку от источника, именуемую как прямая волна, и совокупности волн, попадающих в нее после отражений от границ изолированного объема – отраженная волна.

Плотность энергии Wп в любой точке изолированного объема будет складываться (рис. 6.38) из плотности энергии w прямой волны и плотности энергии Wg при диффузном поле отраженной волны: Wп = w + Wg. Умножив это уравнение на скорость с, получим

Iп=I+4Ig

Интенсивность прямой волны в общем случае определяется формулой (6.28). Выразим плотность потока энергии Ig через мощность источника. При работе источника в изолированный объем постоянно поступает энергия. При мощности источника W отраженный от границ полный поток энергии составит pW, а от единичной площадки pW/S. За единицу времени через единичную площадку границы вследствие поглощения исчезнет количество энергии, равное αIg. Так как в диффузном поле плотность энергии постоянная, то должно соблюдаться равенство рW/S=αIg. Для простоты дальнейших рассуждений здесь предполагается, что коэффициент а значительно больше коэффициента т. Уравнение (6.32) принимает вид

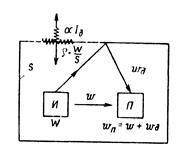
Рис. 6.38. Диффузное поле отраженной волны

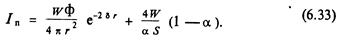
Из полученного выражения видно, что в изолированном объеме плотность потока энергии получает некоторое приращение, которое аналитически обусловлено наличием множителя (1–α)/α, который велик при коэффициенте α близком к нулю.

Защитное устройство бесконечной толщины. Во многих случаях информацию можно получить, исследуя вместо реальной конструкции теоретическое защитное устройство бесконечной толщины, оно представляет собой просто среду, бесконечно простирающуюся в направлении распространения волны. Таким образом, волна из одной среды проходит в другую среду (защитное устройство), предварительно попадая на границу раздела этих сред. При падении на плоскую границу раздела двух разных сред плоская волна частично отражается, частично проходит в другую среду, оставаясь плоской, но меняя при этом свое направление распространения, т. е. преломляясь. Таким образом в общем случае существуют три волны: падающая, отраженная и преломленная (прошедшая).

При прохождении границы раздела сред без поглощения должен соблюдаться закон сохранения энергии: W^- + W˜ = W⁺. Кроме того, на границе должны выполняться специфические для волн данной природы условия: например, для звуковых волн по обе стороны границы должны быть равны звуковые давления – принцип непрерывности звукового давления; для электромагнитных волн на границе раздела двух сред непрерывны тангенциальные составляющие электромагнитного поля. Условие непрерывности при нормальном падении волн можно записать в виде равенства на границе амплитуд поля в среде j и среде j:[um]j=[um]. Усредненный поток энергии можно выразить через интенсивность: W= IS, а интенсивность – через амплитуду и импеданс среды с помощью формулы (6.25). Тогда закону сохранения энергии можно придать виц (рис. 6.39)

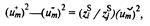
W и т, U т, и т – амплитуда, соответственно, падающей, отраженной и прошедшей волн, a z k = Zk/Sk – импеданс на единицу площади (k = /, у).

В среде i существуют падающая и отраженная волна, которые на границе создают суммарную амплитуду [u,n]i == и^т ⁺ "w» в среде у существует только преломленная волна:

[Urn]} ⁼⁼ иЩ. Условие непрерывности и закон сохранения энергии позволяют найти амплитудный коэффициент отражения Ry и амплитудный коэффициент передачи Тц при' падении волны на границу (/, j) из среды /:

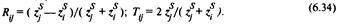
При этом имеем Ту = 1 + 7?у, Ry = –Rj,. Так как значение коэффициента отражения лежит между –I и +1, то значение коэффициента передачи заключено в интервале от 0 до 2 и он всегда положителен. При равных площадях (S, = Sj) соотношения (6.34) примут такой же вид, который можно получить простой заменой ^ на ^, а при равных импсдансах сред to == ^) – заменой ^ на \/S„ (k = /, /). Амплитудные коэффициенты отражения и передачи при нормальном падении волн связаны с соответствующими энергетическими коэффициентами соотношениями:

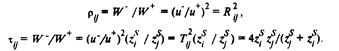
Защитное устройство конечной толщины. В общем случае защитное устройство имеет конечную толщину. При этом волна, падая на защитное устройство, частично отражается, а частично может проходить сквозь него. Отражательную способность защитного устройства характеризуют коэффициентом отражения энергетическим и амплитудным. Прозрачные свойства защитою устройства характеризуют соответствующими коэффициентами передачи. Амплитудные коэффициенты отражения и передачи па границах разных сред будем обозначать соответственно через Ry и t{j. Эти величины определены соотношениями (6.34). Амплитудные коэффициенты отражения и передачи защитного устройства будем обозначать соответственно через R и Г, при этом в комплексной форме

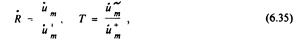
где U⁺_т и U_т^- –соответственно амплитуда падающей и отраженной волны на входе в защитное устройство; U_т –амплитуда волны на выходе из защитною устройства.

Рассмотрим случай, когда гармоническая волна падает из среды 1 (рис. 6.40) на защитное устройство произвольной толщины h, состоящее из среды 2, ограниченной с другой стороны средой з, при этом S₁ = S₂ = S₃. Примем, что импедансы сред соответственно равны Z₁, Z₂, Z₃ волновое поле в среде 2 на длине h затухает по экспоненциальному закону е, где h – коэффициент распространения. При неравных импедансах сред часть энергии на границе (7, 2) отражается обратно в среду 7 в соответствии с формулой (6.34). Амплитуда падающей волны равна и+^п- Обозначив амплитуду отраженной волны через U, имеем: U= R_um.

Другая часть энергии пройдет в среду 2 и, изменившись пропорционально коэффициенту передачи Гц на границе (7, 2), претерпит в среде 2 затухание по закону е² , так что амплитуда волны в среде 2, которую обозначим через U, определится выражением й\ = Т^е^й+т- Эта волна на границе (2, 3) частично отразится и создаст в среде 2 отраженную волну, амплитуда которой с учетом затухания станет равной й^ == ^R^T^e'²^ и частично пройдет в среду J. Амплитуда прошедшей волны будет равна ид = ^^ТчзТ^ ^hu-^m. Волна с амплитудой йч, частично пройдет в среду 7: и^ =Г2l7l27г23^^-2u^⁴m, а частично отразится от границы (7, 2^ и снова будет распространяться в среде 2 в виде волны с амплитудой us = rzi ТЬ^зе"³^-* /и. Процесс отражения и прохождения волн на границе сред (1, 2 и 2, 3) будет продолжаться до полного затухания волн

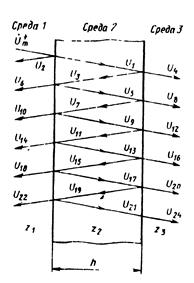
Рис. 6.39. Баланс энергии на границе раздела сред

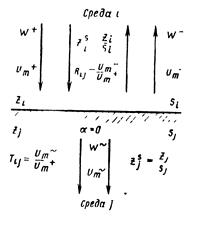
Рис. 6.40. Схема защитного устройства конечной толщины

Суммируя все волны, из которых в среде 7 формируется общая отраженная волна, можно получить для амплитуды этой волны следующее выражение

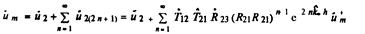
Пользуясь формулой бесконечной геометрической прогрессии, найдем амплитудный коэффициент отражения защитного устройства

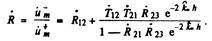
В среде 3 суперпозиция распространяющихся волн создаст волну, прошедшуюсквозьзащитное устройство. Амплитуда этой волны на выходе из защитного устройства

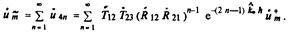
Просуммировав, получим согласно формуле (6.35) амплитудный коэффициент прозрачности защитного устройства конечной толщины:

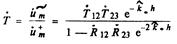
С помощью формул (6.34) преобразуем коэффициенты R и Г квиду:

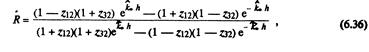
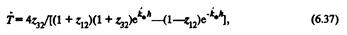
где zi2 ⁼ а/О и 02 = o/q. Полученные соотношения носят общий характери их можно применять при решении задач защиты как от звуковых, так и от электромагнитных полей,

Если по обе стороны от защитного устройства находится одна и та же среда, то импедансы ^и ^ равны. Тоща формулы (6.36) и (6.37) преобразуются к виду:

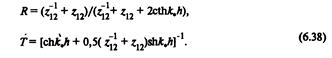
Амплитудные коэффициенты R и Т при нормальном падении волн связаны с энергетическими коэффициентами р и т соотношениями: р = В.², т = Г², эффективность защиты

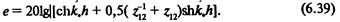
В некоторых случаях для расчета эффективности защиты удобно использовать следующую запись:

е = е. + е + <?., (6.40)

Ж f. Л ^

где ^ = (201g^)8A, ^ = 201g|T U вц = 201g|(l– рце^-2V)! – слагаемые эффективности за счет ослабления волн соответственно в материале защитного устройства, при прохождении границы раздела сред (1, 2) и при многократных отражениях внутри защитного устройства. Так как с увеличением частоты коэффициент h возрастает, то ^ -> 0 и эффективность изоляции высокочастотных полей е w ek •+- е^

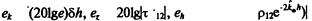
Прогнозирование шума. Условие безопасности при наличии звукового поля можно записать в виде неравенства

L,(f) ^(Д (6.41)

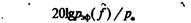
где Lp(f) = 201gp^(/)/A и 1н(/) –соответственно уровни звукового давления и их нормативные значения. Неравенство (6.41) должно выполняться на всех среднегеометрических частогах/== 63,125, 250, 500,1000, 2000, 4000, 80000 Гц и во всех точках рассматриваемого пространства с учетом времени звукового воздействия. Из соотношения (6.26) следует

L^L-L, (6.42)

Референтные значения звукового давления, интенсивности и им-педанса равны: а = 2 • 10'⁵ Па, 1 = 10¹² Вт/м² = 400 Па • с/м.

Характеристический импеданс среды для звука равен произведению скорости звука в среде сна ее плотность p:z = рс. Для атмосферного воздуха при р == 1,29 кг/м³ и с = 331 м/с ^ = 430 кг/(м² • с). В табл. 6.8 приведены значения импеданса г для разных сред.

Таблица 6.8. Плотность, скорость звука и характеристический импеданс для некоторых сред и материалов

Среда, материал	Плотность ρ, кг/м3	Скорость звука с, м/с	Импеданс z= рс, Па∙ с/м
Водород	0,084
Вода			1,45 • 106
Бензин			0,89 • 106
Алюминий			16,5 • 106
Медь			41,1 • 106
Сталь			47,6 106
Стекло		4900...5900	(12...15) • 106
Полистирол			2,94 • 106
Железобетон			11•106
Кирпич			4,1 • 106
Пробка			0,12∙106
Резина (техниче			0,72 • 106
ская)

При распространении звука в атмосфере значение импсданса будет зависеть от температуры и давления. Значение ^ = 400 Па • с/м будуг соответствовать условиям, когда, например, давление и температура будут соответственно равны 0,9 • 10⁵ Па (675 мм рт. ст.) и –27 °С или 1,013 • 10¹⁵ Па и +38,8 °С. Однако при изменении давления и температуры в пределах обычной атмосферы уровень импеданса 2^= lOlg^* незначителен и им пренебрегают, полагая, что Lp(f) = Z//).

Уровень интенсивности или плотности потока энергии можно определить, используя зависимости (6.29), (6.30), (6.33).

Для расчета уровня шума в изолированном объеме используют уравнение (6.33), которое записывают в децибелах в виде

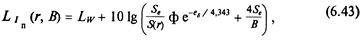
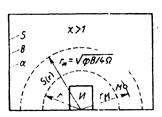
Рис. 6.41. Схема расчета уровня шума в изолированном объеме

де Z/„( г, В) – уровень плотности потока энергии на сферической поверхности радиуса г, образованной телесным углом излучения Q при данном значении постоянной изолированного объема B=aS/(l–а), где S–общая площадь его внутренней поверхности с коэффициентом поглощения а; ^5 – затухание звука (см, пояснения к формуле (6.29), которое в большинстве случаев можно принять равным нулю, S(r) == 4пу^.Сферическая поверхность описывается радиусом г из акустического центра (АЦ). Если источник расположен на плоскости (и = 2п), то АЦ совпадает с проекцией геометрического центра источника на эту плоскость. Угол излучения Q зависит от местоположения источника шума: и = 2тс при расположении источника на плоско-ста; П = я – в двухгранном угле; Q == я/2 – в трехгранном угле, образованном ограждающими стенками. При отсутствии более точных данных углу О соответствует коэффициент направленности ф = (W/ ^)/( W/4nr¹) = 4w/Q.

Формулу (6.43) обычно применяют, коща радиус г > 24пах> гае ^пях – максимальный размер источника.

Чтобы определить уровень шума в точке ^изолированного объема (см. рис. 6.41), в формуле (6.43) следует положить r= /\i. Найденное таким образом значение L^ сравнивают с нормами.

В выражение (6.43) входит коэффициент поглощения а, который зависит от многих факторов, например, от угла падения и частоты. На практике при расчетах по формуле (6.43) используют значения коэффициентов поглощения, полученные при измерениях в трубе или в реверберационной камере, несмотря на то, что их значения могут различаться (например, теоретически при измерениях в трубе а<, 0,95, а для того же случая в реверберационной камере а = 1,2). В практических расчетах коэффициент а вычисляют по правилу: для частот/== 63... 1000 Гц принимают а == ао, где ао определяют по табл. 6.9; для частот /= 2000...8000 Гц коэффициент а вычисляют по формуле: а = « 1–(1–oio)exp(–25/), ще 6 в нужной размерности находят из табл. 6.7, а постоянная

Л

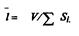
затухания звуковой энергии в объеме Н равна 1= 4 V/ Si .

Таблица 6.9 Коэффициент поглощения а в производственных помещениях

Тип помещения	Среднегеометрическая частота, f, Гц
Машинные за-	0,07	0,08	0,08	0,08	0,08	0,08	0,09	0,09
лы, испытатель-
ные стенды
Механические	0,10	0.10	0.10	0,11	0,12	0.12	0,12	0,12
и металлообраба-
тывающие цехи;
цехи агрегатной
сборки в авиа- и
Судостроительной
Промышленности
Цехи деревооб-	0,11	0,11	0,12	0,13	0,14	0,14	0,14	0,14
работки, посты
управления, ла-
боратории, кон
структорские
бюро

Некоторые ориентировочные значения коэффициента поглощения даны в табл. 6.9. Если стенки изолированного объема изготовлены из п разных материалов, то в выражении (6.43) а есть среднее значение коэффициента звукопоглощения:

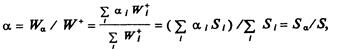
где Wf – усредненный за период поток энергии, падающий на поверхность /-стенки, площадь и коэффициент поглощения которой соответственно равны *У/ и a/; Sa == ^ а/*У/ – эквивалентная площадь i - внутренней поверхности изолированного объема (i = 1, п).

Из уравнения (6.32) следует, что степень диффузного поля может быть охарактеризована отношением 41д//= ^с. Пространство, где ^ < 1 (т. е. вблизи источников шума), называют зоной прямого звука, а пространство, где ^ > 1 (т. е. вдали от источников, вблизи стенок изолированных объемов),– зоной отраженного звука. Условие % = 1 позволяет^задать границу между этими зонами в виде радиуса г, = = ^Вф/(16пг¹) (см. рис. 6.41) и при г» г^ записать выражение (6.43) в виде (^а=0):

lj (г, В) - L(В) = Z.+ ioig(4.y / В). (6.44)

Звукопоглощение. Для уменьшения отраженного звука применяют защитные устройства, обладающие большими значениями коэффициента поглощения, к ним относятся, например, пористые и резонансные поглотители.

Звуковые волны, падающие на пористый материал, приводят воздух в порах и скелет материала в колебательные движения, при которых возникает вязкое трение и переход звуковой энергии в теплоту. Коэффициент звукопоглощения а будет зависеть как от угла падения звуковых волн, так и от частоты. Для пористого поглотителя, находящегося на жесткой стенке, частотная характеристика коэффициента а имеет вид, показанный на рис. 6.42, д. Для усиления звукопоглощения на низких частотах между пористым слоем и стенкой делают воздушную прослойку (рис. 6.42, б). Пористые поглотители изготовляют из органических и минеральных волокон (древесной массы, кокса, шерсти), из стекловолокна, а также из пенопласта с открытыми порами. Для защиты материала от механических повреждений и высыпаний используют ткани, сетки, пленки, а также перфорированные экраны. Последние существенно изменяют характер поглощения звука защитным устройством (рис. 6.42, в).

Резонансные поглотители имеют воздушную полость, соединенную отверстием с окружающей средой. Воздух в резонаторе выполняет роль механической колебательной системы, состоящей из элементов массы, упругости и демпфирования. Если пренебречь рассеиванием звуковой энергии, то импеданс резонатора, равный механическому импедансу (см. формулу (6.18), отнесенному к единице площади, будет равен нулю на частоте со. При импедансе резонатора ^ = 0 коэффициент отражения звукового давления R = –1. Таким образом, снижение шума происходит за счет взаимного погашения падающих и отраженных волн.

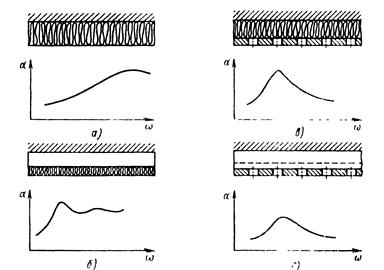
Рис. 6.42. Частотные характеристики коэффициента поглощения:

а–для пористого поглотителя на жесткой стенке; б–для пористого поглотителя с воздушной прослойкой; в –при наличии перфорированного экрана; г–для резонансного поглотителя, образованного перфорированным экраном

Резонансным поглотителем является также перфорированный экран с отверстиями, затянутыми тканью или мелкой сеткой (рис 6.42, г), который существенно меняет характер поглощения. Пористые и резонансные поглотители крепят к стенкам изолированных объемов.

Кроме того, звукопоглощение может производиться путем внесения в изолированные объемы штучных звукопоглотителей, изготовленных, например, в виде куба, которые в производственных помещениях чаще всего подвешивают к потолку.

К хорошим звукопоглощающим материалам относят те, которые на среднегеометрических частотах октавных полос 250, 500, 1000, 2000 Гц имеют коэффициент а, равный или превышающий соответственно значения: 0,2; 0,3; 0,4; 0,5.

Обозначив постоянную изолированного объема до установки поглощающих материалов через Д== (х-5/(1–а), а после установки – В == аД(1 –а) и записав коэффициент защиты в виде: kw = In(r, B)/In{r, В), найдем эффективность звукопоглощения: . /

е = lOlgA^ = L^ (г. В) – Zi„(r, В), (6.45)

где уровни Z/„ (r,B) и L^ (r, В) оп^юделяют по формуле (6.43).

Для вычисления постоянной В имеет смысл коэффициент а выразить через площадь5», на которой предполагается разместить защитные

устройства со средним коэффициентом звукопоглощения, равным о». Эквивалентная площадь внутренней поверхности изолированного объема до установки защитных устройств Дх == а*У== а'(*У–А)4- + a"S^ где а' и а" – средние коэффициенты звукопоглощения поверхностей площадью (S–iS») и S^ эквивалентная площадь после установки защитных устройств Sa ^dS^a^S–S^) + а^. Из этих уравнений находим а == а–(а"–a^S^/Su в тех случаях, когда можно принять aS a"S^ имеем а = Sa(*)/S, где *Уа(*) = = а^ – эквивалентная площадь звукопоглощающих устройств. При внесении в изолированные объемы штучных звукопоглотителей &(*)= ос^ + ^ Sa.(i)fii, где Sa(i} I – экивалентная площадь /-то звукопоглотителя, а/г/ – их число. И < выражений (6.44) и (6.45) видно, что эффективность е в зоне отраженного звука удобно вычислять по формуле:

e=lOig£/R

Требуемая эффективность звукопоглощения определяется по формуле (6.43), исходя из условия безопасности: L//r, В) ^ L». Однако следует учитывать, что практическая реализация звукопоглощения позволяет снижать шум обычно не более чем на б... 8 дБ (в зоне отраженного звука –на 10... 12 дБ).

Звукоизоляция. Звукоизоляция–уменьшение уровня шума с помощью защитного устройства, которое устанавливается между источником и приемником и имеет большую отражающую и (или) поглощающую способность. Обычно роль защитных устройств выполняют глушители шума, экраны или стенки изолированных объемов. Например, защитным устройством является кожух, которым закрывают машины и механизмы, или кабина, в которой находится оператор, управляющий рабочим процессом. Стенки кожухов и кабин изготовляют из листового проката и покрывают изнутри звукопоглощающим материалом. Эффективность звукоизоляции с помощью стенки толщиной h можно определить по формуле (6.39). Если пренебречь затуханием звука в материале, т. е. положить в формуле (6.39) коэффициент распространения А» равным jka, где kz = со/Сз – волновое число, то эффективность

е = 1 Olg[cos²^ 4- 0,25feAi + Zi/^)²sm²^2A],(6.46)

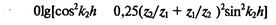
где Zi⁼⁼ pi^i – импеданс воздуха; ^ = рзСз – импеданс материала защитного устройства.

Из выражения (6.46) следует, что эффективность звукоизоляции равна нулю при толщине стенки А==/г^2/2, т. е. кратной половине длины волны (п= 0, 1, 2 ...), а максимальная эффективность будет иметь место, если толщина стенки h = (2п + 1)Х2/4.

Так как для защитного устройства, находящегося в воздухе, всегда выполняется неравенство piCi « рдОг, то для тонкой стенки (h^ « ^2/271) из выражения (6.46) находим

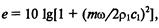
^=101g[l+(wo)/2pici)²], (6.47)

где т == рзА – поверхностная плотность (масса защитного устройства, отнесенная к единице площади).

При достаточно больших частотах единицей в правой части формулы (6.47) можно пренебречь:

е = 20 Ig-^ = 20 lg(w/)–const. ^(6M) 2piCi

Как видно из формулы (6.48), единственным свойством защитного устройства, определяющим эффективность звукоизоляции при принятых допущениях, является поверхностная плотность т. Эффективность звукоизоляции растет с увеличением плотности т и частоты / Константу, входящую в выражение (6.48), определяют, осредняя коэффициент передачи т по углам падения. Если т и / выражены соответственно в кг/м² и Гц, то константа равна 47,5 дБ.

Найдем требуемую эффективность звукоизоляции. По определению

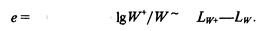
<?= 10 lgl/т == 10 IgW^/y = Lw^–Lw. (6.49)

Будем обозначать параметры, относящиеся к изолированному объему, в котором установлен источник шума мощностью W, индексом 1, а параметры, относящиеся к изолированному объему, где расположен приемник, индексом 2. Суммарная плотность потока энергии t звука, падающего на ограждающие стенки изолированного объема 1, в общем случае складывается из интенсивности W/[S\(r)} прямого звука и плотности потока энергии ^ = wib\ диффузного поля

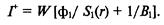
Обозначая через S^ площадь поверхности тех стенок изолированного объема 1, через которые звук излучается в изолированный объем 2, находим падающий поток энергии W^ = -/У и с учетом выражения (6.50) имеем:

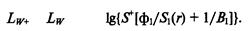
Допустимый уровень Lw"– потока энергии, переданного в изолированный объем, находим из выражения (6.43), полагая 1^(г, В) ^ L^ (e^O)

| Lw ^ zh–io ^[фА/ад + 45^]. (6.52)

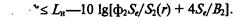
Подставив соотношения (6.49) и (6.51) в формулу (6.52), получим значение требуемой эффективности звукоизоляции:

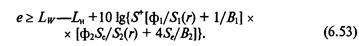
Для точечного источника шума, находящегося в изолированном объеме 7, образованным стенками кожуха (рис. 6.43, а), и излучающего шум в изолированный объем 2 (например помещение), можно в первом приближении принять S^ = 5'i(r)= 5p Тогда из выражения (6.53) требуемая эффективность

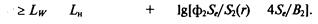
На рис. 6.43, б показано помещение 7, в котором установлен источник шума, отделенное от помещения 2 где расположены рабочие места, стенкой, площадь которой равна 5. Принимая, что в помещении 2 уровень шума во всех точках примерно одинаков (т. е. 2?2/(452(г)) « 1), из выражения (6.53) находим

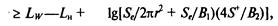
где радиус г равен минимальному расстоянию от акустического центра источника шума до стенки площадью *У\ На рис. 6.43, в показана кабина, защищающая оператора от шума, создаваемого источником в помещении 7. Если кабина расположена на большом расстоянии от источника, то она находится в зоне отраженного звука. Для этого источника из выражения (6.53) находим, что требуемая эффективность

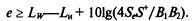
Р и с. 6.43. Схемы снижения шума:

а–изолирующим кожухом; б–звукоизолирующей перегородкой; в –с помощью звукоизолирующей кабины

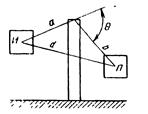
Рис. 6.44. Схема снижения шума экраном

При установке экрана между источником и приемником (рис. 6.44) за экраном образуется звуковая тень. Уровень шума в теневой зоне от точечного источника может быть рассчитан на основе законов дифракции. Эффективность звукоизоляции при защите экраном

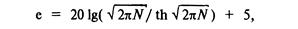
где N–число Френеля; N=£2(a^-b–d)/'k (формула применима при условии N>: –0,2). Кроме того, формулу не рекомендуется применять при малых теневых углах 0. Если не вы полняется указанное неравенство, то е = 0. Расстояние (а + А) складывается из расстояния а от источника до верхней кромки экрана и расстояния Ь от верхней кромки экрана до приемника. Число вберется со знаком минус, если экран расположен ниже визирной линии (расстояние по визирной линии между источником и приемником равно d). Экраны, установленные в производственных помещениях, обычно покрывают с одной или двух сторон поглощающим материалом.

Кожухи и кабины, рассмотренные выше, имеют технологические отверстия (например, отверстия или проходы для воздуха в целях вентиляции), через которые может проникать шум. Во время рабочего цикла ряда установок (компрессоров, двигателей внутреннего сгорания, турбин и др.) через специальные отверстия происходит истечение отработавших газов в атмосферу и (или) всасывание воздуха из атмосферы, при этом генерируется сильный шум. В этих случаях для снижения шума используют глушители.

Система глушения шума включает источник шума, обладающий некоторым внутренним импедансом ^и; источник соединен с помощью трубопровода длиной 1\ с глушителем шума, а трубопроводом длиной /2 – с приемником шума, который характеризуется импедансом излучения ^п. Эффективность глушения определяют по формуле (6.49), полагая, что W^ –усредненная во времени звуковая мощность на входе в глушитель, а IV –на выходе. Конструктивно глушители состоят из активных и реактивных шумоглушащих элементов. Простейшим активным элементом является любой канал, стенки которого покрыты изнутри звукопоглощающим материалом.

Если звуковая мощность в сечении площадью S (рис. 6.45, а) равна W, то плотность потока энергии, падающего на поверхность стенки канала, по формуле (6.31) равна /ц = W/^S. Таким образом, на повер-" хности канала площадью Pdl (где Р – периметр) поглощающая звуковая мощность dW= –oL^PdIn эффективность активного элемента е «1,09аЖУ.

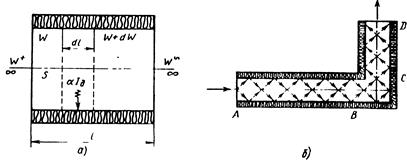
Рис. 6.45. Применение в глушителе поглощающих материалов:

а –схема активного элемента глушителя; б–схема снижения шума при повороте трубопровода,покрытого изнутри звукопоглощающим материалом

Трубопроводы всегда имеют повороты, которые будут снижать шум, если их покрыть звукопоглощающим материалом. Как видно из рис. 6.45, б, на участке АВ существуют преимущественно волны, направленные вдоль оси канала (другие волны будут поглощаться). Изгиб канала будет поглощать или отражать осевые волны назад к источнику. Таким образом, после изгиба останутся преимущественно дифрагиро-ванные волны, которые в значительной мере подавляются на участке CD, так что в конце этого участка останутся ослабленные волны в направлении оси канала.

Реактивный камерный элемент (рис. 6.46) представляет собой участок канала (трубы), на котором внезапно меняется площадь сечения от S\ до So, и образуется камера длиной /. При изменении площади сечения звук отражается. Эффективность камерного элемента можно определить по формуле (6.46), заменив отношение импедансов на отношение площадей [см. формулу (6.34)] и толщину h на длину / камеры (h = k = о/с):

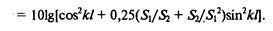
На очень низких частотах, когда kl -> 0 или когда длина глушителя равна V2, X,, ЗХ/2 и т. д., образуются стоячие волны, которые увеличивают давление на концах камерной полости. В результате импеданс трубопровода с поперечным сечением Sh. также увеличивается от значения pc/Sz до значения wpc/&, которое в точности равно импе-дансам входного и выходного трубопроводов, т. е. равно рс/Д. Таким образом, на этих резонансных частотах взаимодействие волн приводит к рассогласованию импедансов и отражению звуковой энергии к источнику шума. На более высоких частотах, когда длина волны \ равна или меньше поперечного размера камеры, эффективность будет зависеть от других параметров (теоретически максимум эффективности достигается при разности диаметров dz–d\ = V2, 3V2, 5V2 и т. д.).

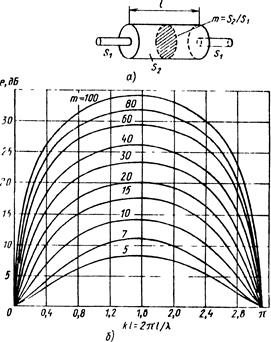Рис. 6.46. Реактивный камерный элемент глушителя: а – схема элемента; б – зависимость эффективности камерного глушителя от длины камеры и отношения площадей

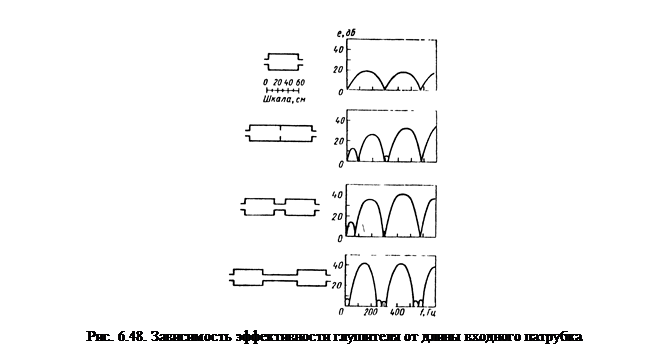
Эффективность е растет с увеличением числа камер и длины соединяющей трубы. Однако уже добавление третьей камеры создает незначительный эффект по сравнению с двумя предыдущими (рис. 6.47).

На рис. 6.48 для сравнения показаны эффективность глушителя, состоящего из двух последовательных камер и эффективность глушителя из двух камер, но со входом или выходом, введенным в полости камер, и оканчивающимися на середине их длины. Эффективность последнего глушителя выше. Изменяя длину входа и выхода, можно варьировать эффективность и частотный диапазон.

Если в спектре шума присутствуют дисперсные составляющие высокого уровня, то эффективность камерных элементов может оказаться недостаточной. В этом случае применяют реактивные элементы резонаторного типа: кольцевые и ответвления (рис. 6.49). Такой глушитель отличается от предыдущих тем, что поток газа через камеру не протекает и она подсоединяется к основному трубопроводу через одно или некоторое количество небольших отверстий или трубок. Этот тип глушителя называют объемным резонатором или глушителем Гельм-гольца. Резонансные частоты определяются размерами отверстий и подсоединенным объемом. Предполагается, что линейные размеры подсоединенного объема меньше 1/10 длины волны на всех рассматриваемых частотах. Если это условие нарушается, то надо принимать во внимание движение волн в резонаторе. Ситуация становится похожей на глушитель, рассмотренный выше. Эффективность объемного глушителя.

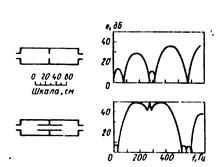Рис. 6.47. Зависимость эффективности глушителя от числа камер и длины соединительной трубы

натора; (3 = s\c/it^v– безразмерное реактивное сопротивление резонатора; *Si и sq –соответственно площадь трубопровода и суммарная площадь отверстий;^ –резонансная частота; V–объем резонатора. При резонансе (f^fo) эффективность зависит только от величины ос и может быть записана в виде

e=20lg[(α+0,5)/α]

При а < 0,25 и при частотах намного больших или меньших частоты fо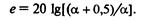

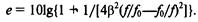
На рис. 6.50 показана эффективность глушителя рассматриваемого типа при а = 0,5р.

Эффективность глушителя, синтезированного из типовых элементов, может быть определена по формуле:

– эффективность i-го шумоглушащего элемента.

Рис. 6.49. Схемы глушителей резонаторного типа: а –кольцевые; б–ответвления

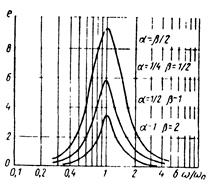
Рис. 6.50. Эффективность резонаторного глушителя при α = 0,5р

Экранирование электромагнитных полей*. Электромагнитное поле имеет зоны индукции и излучения, которые для элементарных излучателей (диполей) в воздух определяются соответственно неравенствами:

Обычно считают, что на расстоянии от источника, не большем длины волны – зона индукции. Например, для частот 10⁹ и 10⁶ Гц расстояние, которое определяет зону индукции, меньше 0,3 м и 300 м.

Для антенн зону излучения обозначают неравенствами: r > e² / λ и r > 3/λ, где l – размер антенны. В зоне излучения поле практически принимает плоскую конфигурацию и распространяется в виде плоской волны, составляющие которой равны:

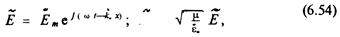
е«

где ε*=ε-jς/ω – комплексная диэлектрическая проницаемость среды; ε иμ. –абсолютные проницаемости соответственно диэлектрическая и магнитная;ς–удельная проводимость среды; комплексное волновое число k*= ω√με*.

Сравнивая выражения (6.24) и (6.54), видим, что импеданс среды электромагнитному полю z = √με*. С учетом формулы (6.54) найдем, что для непроводящей среды ς = 0)

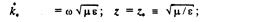
для проводящей среды (ε = 0)

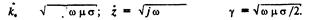
Здесь термин «изоляция» заменен термином «экранирование»,который обычно используется в специальной литературе.

В табл. 6.10 приведены ориентировочные значения волнового числа и импеданса

для металлов. Для вакуума импеданс равен Z0 = √μ∕ε120π,Ом, где μо и εo – so соответственно электрическая и магнитная постоянные: ε = 1/(36π∙10^-9)=8,85 • 10^-12 ф/м μо = 4л •10'⁷ Гн/м. В зоне индукции импеданс среды зависит от источника.

Таблица 6.10. Характеристика металлов, применяемых для экранирования ЭМП

Металл	Электрическая проводимость	Магнитная проницаемость μ/μо	Коэффициент распространения	Импеданс
	ς • 106. См/м		│К*│=√ωμς, мм'1	│Z│=√ω∕μς
Медь	57,1		21,2•10'З7√f	0,372 • 10'6 √f
Алюминий	34.5		16,4 .10'3 √f	0,478 • 10"6 √f
Сталь	7,2		75,4. 10'3 √f	10,47 • 10'6 √f
Свинец	4,8		6,2 • 10'3 √f	1.28 • 10'6 √f

При определении электромагнитного поля сложных источников их разбивают на элементарные, а затем используют принцип суперпозиции полей. Импеданс среды для поля элементарного электрического излучателя

Z=Z0(1+jkr+1/jkr)(1+jkr), (6.57)

Импеданс среды для поля элементарного магнитного излучателя

Z=Z0(1+1/jkr)/(1+jkr+1/jkr), (6.58)

Из выражений (6.57) и (6.58) видно, что вблизи источника, т. е. в зоне индукции (kr «1), импеданс среды преимущественно электрическому полю

Z=ZE≈Z/jkr (6.59)

импеданс среды преимущественно магнитному полю

Z=ZH≈jk/Z0 (6.60)

С увеличением расстояния от источника импеданс ZE уменьшается, а импеданс ZHувеличивается (рис. 6.51). Оба импеданса будут стремиться к одному значению, которое они достигают в зоне излучения Z=Z^EH=Z0.

Различают экранирование магнитного, электрического и электромагнитного (плоская волна) полей. В большинстве случаев с двух сторон от экрана находится одна и та же диэлектрическая среда – воздух, и эффективность экранирования, пользуясь формулой (6.39), можно записать в виде

E=20lg│ch_k*h│+20lg│1+0,5(Z2/Z1+Z1/Z2)thk*h│

Чтобы произвести расчет по этой формуле, кроме толщины экрана h необходимо знать коэффициент распространения k* и импедансы Z1 и Z2. Так как экран обычно изготовляют из металла, то с учетом зависимостей (6.27) и (6.56) коэффициент распространения k* и импеданс Z2 будут равны: k* = √jwμ2ς2. Более сложно определяется импеданс Z1. В зоне излучения импеданс диэлектрической

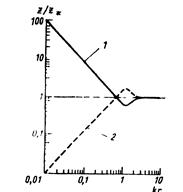
Рис. 6.51. Импеданс среды для элементарных излучателей в зависимости от расстояния от источника:

среды – воздуха – будет равен (для воздуха μ≈μ0, ε≈ε) Z1=Z^EH=√μ1/ε1≈√μ0ε0≈ 377 Ом. Однако в зоне индукции импеданс Z1 зависит не только от вида основной составляющей электромагнитного поля |см. формулы (6.59) и (6.60)]. Он определяется также формой конструкции экрана (рис. 6.52). С учетом формы импеданс Z1 при экранировании электрического поля записывают в виде

Z1=Z1^E=Z*/jkr*m=1/jωε1r*m

а при экранировании магнитного поля в виде Z1 = Z1^H=jk1r*mZ*=jωμ1r*m,

где т = 2 при r* = l/2 для плоского экрана; т = 1 при r* = р –для цилиндрического экрана; т = 1/√z при r* = r–для сферического экрана (см. рис. 6.52).

Тогда при k*h, что обычно достигается на низких частотах (f< 10⁴ Гц), chk*h ≈ 1, a thk*h ≈k*h и эффективность экранирования электрического поля (Z1^E/Z2>Z2/Z1^H)

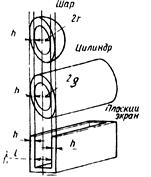
Рис. 6.52. Конструкции экранов

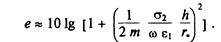
Эта эффективность будет большой на низких частотах, а в диапазоне относительно высоких частот е → 0.

При экранировании магнитного поля необходимо учитывать особенности материала, из которого изготовлен экран. Обычно для магнитных металлов (сталь, пермаллой, феррит)Z1/Z2^H>Z1^H/Z2, а для немагнитных металлов (медь, алюминий, свинец) Z1^H/Z2 > Z2/Z1^H. Тогда для защитных устройств из магнитных металлов эффективность экранирования.

Она не зависит от частоты. Для защитных устройств из немагнитных металлов.

Эта эффективность зависит от частоты и при частоте ω→0 тоже стремится к нулю.

В области относительно высоких частот (10⁴ <f, Гц < 10⁹) эффективность экранирования удобно определять* по формуле

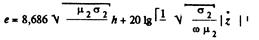
Из соотношения импедансов следует, что амплитудные коэффициенты [формула (6.38)] для плоского Tn, цилиндрического Tц и сферического Тc экранов при Z1>Z2 и имеют приблизительно следующее соотношение: Tn:Tц:Tс = 1:2:3. Это соотношение справедливо для экранов, изготовленных из одинакового материала и имеющих равную толщину стенок, причем расстояние между параллельными пластинами плоского экрана равно диаметру сферического или цилиндрического экранов (l = 2r или 2p). Таким образом, если эффективность экранирования плоским экраном принять за исходное значение en = 20lg1/Tn , то эффективность экранирования цилиндром ец = 201g |1/Tц| = 201g|l/Tn| = en–20 lg 2 ≈ Сп–6 дБ, а эффективность экранирования сферой eс= en–9,5 дБ. При экранировании магнитного поля магнитными материалами (Z2>Z1) соотношение амплитудных коэффициентов передачи будет иметь обратную закономерность Тn:Тц:Тe = 1:1/2:1/3. На практике полученными соотношениями пользуются при определении, например, эффективности цилиндрического экрана по формулам плоского.

В области СВЧ, охватывающей дециметровые, сантиметровые и миллиметровые волны (f ^ 10⁹...10¹⁰ Гц), длина волны λ соизмерима с диаметром экрана d, т. е. λ≥d, и эффективность экранирования носит колебательный характер (рис. 6.53). В этой области импеданс Z1при экранировании

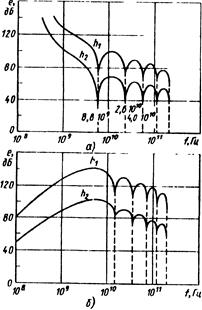
Р и с . 6.53. Колебательный характер эффективности экранирования ЭМП в диапазоне СВЧ:

а – электрическое поле; б – магнитное поле; h1 - 0,01мм, h₂ = 0,001мм, r = 5 мм

магнитного и электрического полей цилиндрическим экраном следует определять по формулам:

(6.63)

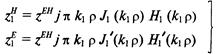
где Jn(u и Нп(и) – функции Бесселя* соответственно первого и третьего рода, порядка п (штрихом отмечены производные). С учетом соотношений (5.63) эффективность экранирования рассчитывают по формуле (6.61), при этом надо иметь в виду, что во многих случаях можно принять Z1/Z2<<1 и пренебречь этим слагаемым.

При наличии в экране для радиоэлектронной аппаратуры отверстий или щелей, возникающих вследствие несовершенства его конструкции и технологии изготовления, среднюю эффективность экранирования можно определить по эмпирической формуле

(6.64)

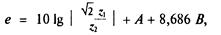
где импеданс Z1 = Z1^H при экранировании электрического поля; Z1≈Z1^H при экранировании магнитного поля; импеданс | Z2│ =│ ωμ₂σ2│; слагаемые А и множитель В = 2πh/l учитывают негерметичность экрана

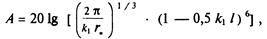
где r*=0,62V^1/3 – эквивалентный радиус экрана любой геометрической формы (V–внутренний объем экрана); l–наибольший размер отверстия (щели) в экране; k₁=ω√μ0ε0 . Формула (6.64) применима в диапазоне частот, пока k_l < 2, l > 0.

Для защиты от ЭМП обычно применяют металлические листы, которые обеспечивают быстрое затухание поля в материале. Однако во многих случаях экономически выгодно вместо металлического экрана использовать проволочные сетки, фольговые и радиопоглощающие материалы, сотовые решетки.

Эффективность экранирования электрического поля при использовании проволочных сеток

е =10lg│Z^E/Z│+A+8,686C

* Обычно функцию Н1(и) находят по формуле: H1(и) = J1(u) + jY(u). Чтобы найти производную, можно использовать соотношение: Q1(Z) = Q0(u)–1/2Q(u), где и означает любую функцию Y, Н или любую их линейную комбинацию. Функции Бесселя даны в виде таблиц в справочниках [6.1].

Здесь слагаемое А означает то же, что в выражении (6.64) (k1l< 2), а множитель С и величину z при заданном диаметре провода d и шаге s сетки рассчитывают по формулам: С= πd/(s–d), z =l/G2h*, где эквивалентная толщина сетки L*=πd²/4s.