Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор
Билет 3
Потенциалом данной точки поля называется работа, которую затрачивает электрическое поле, когда оно перемещает положительную единицу заряда из данной точки поля в бесконечно удаленную точку. Связь потенциала и напряженности: Е=-grad 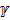 т.е. напреженноть поля = градиенту потенциала со знаком мнус. Минес показывает что вектор направлен в сторону убывания потенциалов.
т.е. напреженноть поля = градиенту потенциала со знаком мнус. Минес показывает что вектор направлен в сторону убывания потенциалов.
эквипотенциальными поверхностями- поверхностями, во всех точках которых потенциал 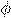
имеет одно и то же значение.
точечным зарядом, то его потенциал 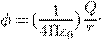
Свойства эквипотенциалей:
1) Работа по перемещению заряда вдоль эквипотенциальной линии (поверхности) равна нулю, т. к. 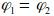 .
.
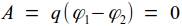
2) Силовые линии поля в каждой точке ортогональны к эквипотенциальной линии (поверхности).
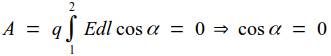
Билет 4
Теорема остроградского-гауса
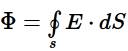
Теорема Остроградского-Гаусса:
Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
Т. К. U одинакова поля по всей сфере одинакова и равна
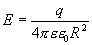 Силовые линии направлены по радиусам, т.е. перпендикулярны поверхности сферы
Силовые линии направлены по радиусам, т.е. перпендикулярны поверхности сферы 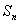 , следовательно
, следовательно
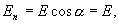 .к.
.к. 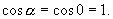
Тогда поток напряженности 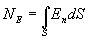 будет равен
будет равен

Используя формулу напряжённости, находим
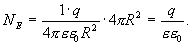 | (13.6) |
Окружим теперь сферу произвольной замкнутой поверхностью S’. Каждая силовая линия, пронизывающая сферу, пронижет и эту поверхность. Следовательно формула (13.6) справедлива не только для сферы, но и для любой замкнутой поверхности. Если произвольной поверхностью окружаем n зарядов, то очевидно, что поток напряженности через эту поверхность равен сумме потоков, создаваемых каждым из зарядов, т.е.
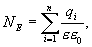
или
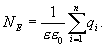 | (13.7) |
Таким образом, полный поток вектора напряженности электростатического поля через замкнутую поверхность произвольной формы численно равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности, поделенной на 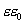 . Это положение называется теоремой Остроградского - Гаусса. С помощью этой теоремы можно определить напряженность полей, создаваемых заряженными телами различной формы.
. Это положение называется теоремой Остроградского - Гаусса. С помощью этой теоремы можно определить напряженность полей, создаваемых заряженными телами различной формы.
Билет 5
Основная особенность проводников – наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника. Типичные проводники – металлы.
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
|
Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика 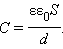 ε0 —(ε0 = 8.854·10−12 Ф/м) электрическая постоянная, ε — относительная диэлектрическая проницаемость. S — площадь одной обкладки, d — расстояние между обкладками
ε0 —(ε0 = 8.854·10−12 Ф/м) электрическая постоянная, ε — относительная диэлектрическая проницаемость. S — площадь одной обкладки, d — расстояние между обкладками
| Параллельное соединение конденсаторов. C = C1 + C2 |
Последовательное 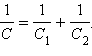 |
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
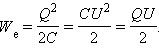
разность потенциалов 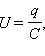 при переносе каждой порции Δq внешние силы должны совершить работу
при переносе каждой порции Δq внешние силы должны совершить работу 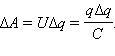
Билет 6 Эл ток. И его характеристики
Эл. Ток - непрерывное упорядоченное движение свободных носителей электрического заряда.
I – скалярная физическая величина, равная отношению заряда Δq, переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени Δt, к этому интервалу времени:
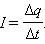 |
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
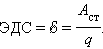 |
Билет 7 Закон ома
Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
| |
| |
Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи. 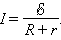
Билет 8
Работа тока- это работа электрического поля по переносу электрических зарядов вдоль проводника; А=U*I*t=I^2Rt=U^2/R*t
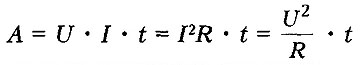
Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого работа совершалась.
Это соотношение выражает закон сохранения энергии для однородного участка цепи.

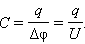
 = Δφ12 +
= Δφ12 +