Тема: Химическая кинетика.

Теоретический материал к занятию:

Химическая кинетика изучает скорости химических реакций, их зависимость от различных факторов и механизмы реакций. Последовательность и характер стадий химических реак­ций называют механизмом реакции.

По механизму различают простые и сложные реакции.

Простые реакции осуществляются посредством однотипных элементарных актов.

Под элементарным актом понимают единичный акт взаимодействия или превращения частиц, в результате которого образуются новые частицы продуктов реак­ции или промежуточных соединений. В элементарном акте принимает участие одна или две частицы (описаны единичные случаи одновременного взаимодействия трех частиц).

Для осуществления сложных реакций необходимы разнотипные (не менее двух) элементарные акты. Различают следующие типы сложных реакций: па­раллельные, последовательные, сопряженные, цепные. Для параллельных реакций характерно протекание нескольких процессов с участием одних и тех же исходных веществ. Эти процессы завершаются образованием разных продуктов реакции. Скорость параллельных реакций определяется наи­более быстрой стадией В последовательных реакциях образо­вание конечного продукта реакции из исходных веществ происходит не непосредственно, а обязательно через ряд промежуточных продуктов. Скорость последовательной реакции определяется наиболее медленной стадией , которая называется лимитирующей стадией. Некоторые сложные реакции состоят как из последователь­ных, так и параллельных реакций.

Скорость химической реакции (v) определяется изменением концентрации Δс реагирующих веществ (или продуктов реакции) в единицу времени. Размерность скорости химической реакции — концентрация/время: dim v = L^-3T^-1N, наиболее употребляемая единица из­мерения — моль на литр-секунду [моль/(л∙с)].

Скорость химической реакции в общем случае не яв­ляется постоянной в течение всего времени ее протекания. Рассмотрим обратимую реакцию:

аА+ bB ↔ dD + fF

Скорость прямой реакции (образование веществ D и F) уменьшается по мере расходования исходных ве­ществ (А и В), а скорость обратной реакции будет уве­личиваться по мере накопления продуктов реакции (D и F). В связи с этим в химической кинетике пользуются понятием средней скорости в данном интервале времени Δ t:

Δc

v_ср = ± ——

Δt

Истинная скорость (в любой момент времени) определяется первой производной концентрации по времени:

dc

v_ист= ± ——

dt

Скорость химической реакции зависит в первую оче­редь от природы реагирующих веществ. Скорость гомо­генной реакции зависит от концентрации реагентов, а гетерогенных — от площади соприкасающихся фаз, т. е. степени дисперсности. Скорости всех реакций зависят от температуры, многих реакций — от присутствия ката­лизаторов.

Зависимость скорости химической реакции от кон­центрации описывается кинетическим уравнением. На­пример, для реакции:

аА+ bB ↔ продукты

v = kc^p(A)c^q(B)

где p, q — эмпирические (найденные эксперимен­тальным путем) коэффициенты, не обязательно совпа­дающие со стехиометрическими коэффициентами а и b; k - константа скорости реакции, размерность которой зависит от значений p и q.

Константа скорости зависит от тех же факторов, что и скорость химической реакции, но не зависит от кон­центрации реагирующих веществ.

Величина р +q определяет порядок кинетического уравнения реакции, который показывает, каким образом скорость реакции зависит от концентрации реагентов. Порядок кинетического уравнения может принимать зна­чения 0, 1, 2 и более, он может быть также дробным.

Важной характеристикой реакции является период полупревращения t_0,5 — время, за которое в реакцию вступает половина исходного вещества. Для радионуклидов аналогичная величина называется периодом полу­распада.

Кинетические расчеты позволяют ответить на следую­щие вопросы:

1) сколько времени требуется для уменьшения кон­центрации исходного вещества до заданного уровня? (Так, например, можно определить оптимальные проме­жутки времени между приемами лекарственного сред­ства);

2) какой будет концентрация исходного вещества по истечении заданного промежутка времени? (Так оценива­ется, например, остаточное количество токсиканта.)

Для решения этих вопросов используют кинетические уравнения. Обозначим через c_о начальную концентрацию реагента, через c_t — концентрацию реагента в момент времени t.

Для реакций нулевого порядка:

dc

- —— = k

dt

откуда c₀ — c_t = kt

c₀

t_0,5 = —

2k

dim k = L^-3T^-1N, единица измерения—моль на литр-секунду [моль/(л∙с)].

_____________________________

Для реакций первого порядка:

dc

- —— = kt

dt

c₀

откуда ln — = kt

c_t

ln2 0,69

t_0,5 = — = ——

k k

dim k = T^-1, единица измерения—секунда в минус пер­вой степени (с^-1).

_____________________________

Для реакций второго порядка:

dc

- —— = kc²

dt

1 1

Откуда — - — = kt

c₀ c_t

t_0,5 = ——

c₀k

dim k = L³T^-1N^-1; единица измерения—литр на моль-секунду [л/(моль∙с)].

_____________________________

Из приведенных уравнений можно сделать следующие выводы:

1) величина константы скорости уравнения первого порядка не зависит от способа выражения концентрации, а констант нулевого и второго порядков зависит. Напри­мер, если концентрацию выразить не в моль на литр, а в миллимоль на литр, то величина константы скорости кинетических уравнений нулевого порядка увеличится в 1000 раз, а величина константы скорости кинетических уравнений второго порядка в 1000 раз уменьшится;

2) величины констант скорости кинетических уравне­ний всех порядков зависят от выбранной единицы вре­мени. Например, если время выразить не в секундах, а в минутах, то величины констант возрастут в 60 раз;

3) период полупревращения реакций первого поряд­ка не зависит от начальной концентрации реагента, пе­риод полупревращения реакций нулевого порядка воз­растает при увеличении с_о, а реакций второго порядка уменьшается. Анализируя зависимость периода полу­превращения реакции от начальной концентрации реа­гента, можно определить порядок реакции.

Скорость реакций зависит от температуры. В соответствии с эмпирическим правилом Вант -Гоффаскорость большинства реакций увеличивается приблизительно в 2 - 4 раза при увеличении температу­ры на 10 °С:

k_T+ΔT = k_Tγ^ΔT/10

где γ — температурный коэффициент константы скорос­ти реакции.

Многие каталитические реакции не подчиняются это­му правилу, для большинства из них γ < 2. Почти все биохимические реакции осуществимы только в присут­ствии ферментов, следовательно, почти все они не под­чиняются данному правилу. Кроме того, при увеличении температуры свыше определенного значения (45 - 50 °С) биохимические реакции резко замедляются, а затем ос­танавливаются, что связано с инактивацией ферментов при высоких температурах.

Более точную зависимость скорости химической реакции от температуры устанавливает уравнение Аррениуса:

k = k₀e^{-Ea /RT}

где Е_а – энергия активации реакции; k₀ – предэкспоненциальный множитель, пропорциональный числу столкновений реагирующих частиц.

Энергия активации реакции Е_а - энергетический барьер, кото­рый должны преодолеть исходные вещества по пути пре­вращения в продукты реакции (рис. 3-1). Dim E_a = L²MT^-2N; единица измерения— джоуль на моль (Дж/моль).

Уравнение Аррениуса для двух температур имеет следующий вид:

k ₂ E_a

ln ¾¾ = ¾¾ (1/T₁- 1/Т₂)

k₁ R

или

k ₂ E_{a Δ} T

ln ¾¾ = ¾¾¾¾

k₁ R T₁Т₂

где k₁ и k₂ – константы скорости при температурах T₁ и T₂, соответственно.

Скорость многих реакций зависит от присутствия веществ, не расходующихся в ходе реакции; такие реакции называются каталитическими. Под катализом понимают изменение скорости хими­ческих реакций в присутствии веществ, которые после завершения реакции остаются в неизменном виде и ко­личестве. Увеличение скорости реакции называют поло­жительным катализом, уменьшение — отрицательным катализом, или ингибированием. Катализа­торами называют вещества, которые вы­зывают положительный катализ; вещества, замедляю­щие реакции, называют ингибиторами.

Катализатор уско­ряет только термодинамически возможную реакцию, причем ускоряет как прямую, так и обратную реакции. Таким образом, катализатор ускоряет достижение состояния химического равновесия в системе, не смещая положение равновесия.

Механизм дей­ствия катализатора заключается в изменении пути процесса превращения реагентов в продукты. Новый путь характеризуется меньшим энергетическим барьером, т. е. меньшей энергией активации.

Величина ΔЕ_а служит критерием эффективнос­ти катализатора. Если условно принять, что величины предэкспоненциальных множителей каталитической и некаталитической реакций одинаковы (на самом деле они отличаются), то в соответствии с уравнением Аррениуса получим следующее уравнение:

k’

ΔE_a = RT ln—

k

где k’ и k — константы скорости каталитической и нека­талитической реакций соответственно. Это уравнение можно использовать для прибли­зительной оценки изменения скорости реакции при вве­дении в систему катализатора.

Перед решением задач рекомендуется выучить следующие основные понятия темы:

1) скорость химической реакции;

2) константа скорости химической реакции;

3) период полупревращения и период полураспада;

4) порядок и молекулярность реакции;

5) температурный коэффициент скорости реакции;

6) энергия активации.

Уметь применять:

1) кинетические уравнения химических реакций разного порядка;

2) зависимость константы скорости химической реакции от различных факторов;

3) методы определения значения энергии активации;

4) математическое выражение правила Вант-Гоффа;

5) уравнение Аррениуса;

6) связь между энтальпией реакции и энергией активации прямой и обратной реакций.

Обратить внимание на то, что:

1) порядок реакции определяют, сопоставляя изменение величин начальной концентрации (с_о) и периода полупревращения (t_0,5). Реакции, для которых наблюдается прямая зависимость между изменениями значений с_о и t _0,5, относятся к реакциям нулевого порядка; реакции с обратной зависимостью величин с_о и t _0,5 - к реакциям второго порядка; реакции, в которых t _0,5 f (с_о) - к реакциям первого порядка;

2) единицы измерения константы скорости зависят от порядка кинетического уравнения реакции;

3) для реакций первого порядка молярные концентрации могут быть заменены любым другим способом выражения состава системы (массовая доля, массовая концентрация и др.), но обязательно одинаковыми для с_о и с_t;

4) единицы измерения величин Е_а и произведения RT, входящих в уравнение Аррениуса :

k = А×е-Е_а/RT,

должны совпадать, т.к. их отношение стоит в показателе степени и должно быть безразмерной величиной;

5) приращение температур Dt = t₂- t₁(DТ = Т₂- Т₁) в математическом выражении правила Вант-Гоффа:

v ₂= v ₁× 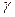^t₂^-t₁^/10

или

k ₂= k ₁× 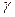^t₂^-t₁^/10

может иметь единицы измерения как в °С, так и в К, и следовательно, 10, стоящая в знаменателе показателя степени температурного коэффициента γ, тоже может иметь единицы измерения либо в °С, либо в К.

7) В уравнении:

k ₂ E_a

ln ¾¾ = ¾¾ (1/T₁- 1/Т₂)

k₁ R

единицы измерения величины Е_а должны быть Дж/моль, т.к. единицы измерения газовой постоянной R - Дж/(моль× К) и в левой части уравнения стоит безразмерная величина k ₂/k ₁.

Учесть, что можно рассчитать:

1) энергию активации Е_а, если известны значения k₁, k₂;

2) константу скорости химической реакции при любой температуре;

3) такие кинетические характеристики, как температурный коэффициент Вант-Гоффа, период полупревращения.