Время выхода частицы из потенциальной ямы

Благодаря тепловому движению у частицы имеется вероятность получить энергию, достаточную для выхода из потенциальной ямы глубиной А, или для преодоления потенциального барьера высотой A. Получим характерное время выхода τ.

Используем определение плотности потока и для одной частицы получаем

.

Подставляем (П.5.12)

,

находим

, (П.5.14)

t₀ – характерное время выхода при . Закон Аррениуса (1889 г.) – время выхода частицы возрастает экспоненциально с ростом глубины ямы. Квантовая механика подтвердила этот вывод.

Сванте Август Аррениус (1859–1927)

Аррениус – шведский физико-химик и астрофизик, лауреат Нобелевской премии по химии 1903 г. Разработал теорию проводимости электролитов на основе диссоциации молекул растворенного вещества на ионы. Заложил основы химической кинетики. В 1896 г. обосновал роль углекислого газа в парниковом эффекте атмосферы. Излучение Солнца с температурой ~ 5000 К в оптическом и ближнем инфракрасном диапазоне (0,4–1,5) мкм проходит через атмосферу к земле. Тепловое излучение земли с температурой ~ 300 К, лежит в дальнем инфракрасном диапазоне (8–28) мкм и поглощается газами и . В результате входящая в атмосферу энергия превышает выходящую энергию, температура нижних слоев атмосферы повышается. Парниковый эффект у Земли в настоящее время , у Венеры – . Аррениус высказал также гипотезу о панспермии – зарождение жизни на Земле вызвано живыми спорами, попавшими на Землю из космоса с других планет. Сейчас эта гипотеза считается наиболее вероятной.

Распределение Больцмана

Рассматривается распределение частиц идеального газа по координатам при температуре Т. При отсутствии внешнего поля все точки объема с газом равновероятны и концентрация частиц не зависит от координат. В стационарном потенциальном поле частица имеет потенциальную энергию 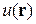и на нее действует сила

, ,

направленная в сторону быстрейшего уменьшения потенциальной энергии. Сила перемещает частицы газа в указанном направлении, но их разбрасывает тепловое движение. Конкуренция этих тенденций создает равновесное распределение концентрации частиц по координатам .

Получение распределения

Для частицы идеального газа используем каноническое распределение по фазовому пространству (2.17)

.

В гамильтониане

слагаемые с импульсами и координатами разделены, поэтому разделяются распределения по импульсам и координатам

.

Для координат получаем распределение Больцмана

, (2.55)

где

– вероятность обнаружения частицы в элементе объема ;

– число частиц в элементе объема ;

N – число частиц в объеме сосуда V;

– потенциальная энергия частицы во внешнем поле.

Нормировка вероятности

дает постоянную

.

Из (2.55) получаем

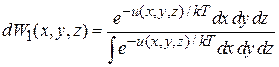. (2.55а)

Если потенциальная энергия зависит от одной координаты , то интегрируем (2.55а) по x и y, и находим

, (2.55б)

где

– вероятность обнаружения частицы в интервале ;

– плотность вероятности, т. е. вероятность обнаружения частицы в единичном интервале около z;

N – число частиц в сосуде.

Число частиц в интервале равно

(2.56)

Мысленно выделяем в объеме газа цилиндр с образующей вдоль z, с поперечным сечением S, и числом частиц . В интервале с объемом число частиц

,

где концентрация частиц

. (2.56а)

Формула Больцмана

Объект. Газ в однородном поле тяжести. Сила mg действует на частицу вниз. Тепловая энергия раскидывает частицы по разным высотам. Концентрация уменьшается с высотой z.

Количественное описание. Потенциальная энергия частицы

,

где m – масса частицы; . Для концентрации получаем из (2.56а) формулу Больцмана

, (П.6.1)

где – концентрация при . При

находим

,

где – основание неперовых логарифов. С ростом температуры растет, уменьшается число частиц на малых высотах и увеличивается число частиц на больших высотах. Площадь под кривой распределения не зависит от температуры.

Если частицы заполняют цилиндр 0 £ z < ¥ с поперечным сечением S, тогда число частиц

.

Получаем концентрацию при

,

и около точки z

.

Площадь под кривой

.

Вероятность обнаружить частицу в интервале

. (П.6.2)

Среднее положение частицы

,

где использовано

,

.

Число частиц в цилиндре

. (П.6.3)

Средняя потенциальная энергия частицы с учетом равна

.

Этот результат следует также из теоремы о распределении тепловой энергии по степеням свободы. Для одной степени свободы используем (2.38) и (2.39)

,

.

Для потенциальной энергии подставляем и находим .

Частные значения. При T = 300°К для воздуха m = 29 кг/кмоль получаем . Число частиц в столбе воздуха с единичным поперечным сечением выражаем через давление . Для Р = 760 мм р.с. находим число частиц в столбе воздуха единичного поперечного сечения

.

Из (П.6.3) получаем концентрацию молекул у поверхности земли – число Лошмидта

.

Для сравнения концентрация электронов проводимости металла .

Иоганн Йозеф Лошмидт (1821–1895)

Газ в центрифуге

Объект. Центрифуга – цилиндрический сосуд с газом радиусом R, длиной образующей H, вращается вокруг оси с угловой скоростью w. В системе отсчета сосуда на частицу действует центробежная сила инерции, направленная от оси вращения. В результате концентрация газа увеличивается с удалением от оси. Тепловое движение разбрасывает частицы по всему объему сосуда, конкурируя с центробежной силой. Получим радиальное распределение частиц, пренебрегая силой тяжести.

Количественное описание. В системе отсчета, связанной с вращающимся сосудом, центробежная сила

создает потенциальную энергию. Используя

,

,

находим потенциальную энергию частицы массой m, находящейся на расстоянии r от оси:

.

Распределение Больцмана (2.55)

в цилиндрических координатах

,

имеет вид

.

Интегрируем по z и φ, и получаем вероятность нахождения частицы в цилиндрическом слое радиусом r толщиной dr

(П.6.4)

Вероятность найти частицу газа в единице объема на расстоянии r от оси

,

где объем цилиндрического слоя

.

Концентрация частиц

,

где N – число частиц в центрифуге. Учитывая (П.6.4), получаем

, (П.6.5)

где

– концентрация на оси вращения;

– увеличивается при удалении от оси.

Условие нормировки на число частиц

с учетом (П.6.5) дает

. (П.6.6)