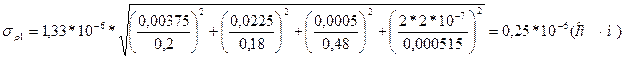Среднее значение диаметра проволоки

ОТЧЕТ

ЛАБОРАТОРНАЯ РАБОТА №1

«оценка точности прямых и косвенных измерений»

Выполнила:

Студентка гр. ИЗБ-11-1

Богатырева Екатерина

Проверил:

проф. Мустафаев А.С.

Санкт-Петербург

2012г.

Цель работы: провести прямые и косвенные измерения физических величин. Выполнить оценку точности измерений.

Общие сведения

Сопротивление [R] – величина, характеризующая сопротивление проводника электрическому току. Зависит от формы, размеров, а также свойств материала, из которого проводник изготовлен. Сопротивление однородного цилиндрического проводника:

R = ρl / S, [Ом]

где l - длина проводника; S - площадь его поперечного сечения;

r - удельное сопротивление.

Удельное сопротивление [r] характеризует способность вещества проводить электрический ток и зависит от химической природы вещества и условий, в которых находится проводник.

r = RS / l , [Ом*м]

Сопротивление [R] вычисляется по измеренным значениям напряжения U и тока I согласно закону Ома для участка цепи:

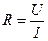
Прямые измерения – такие измерения, при которых значение искомой величины непосредственно регистрируется по показаниям измерительного прибора. (Такие физические величины как l, d, U, I можно измерить непосредственно соответствующими приборами)

Косвенные измерения – такие измерения, при которых физическая величина выражается посредством формулы через измеряемые величины. (Величина удельного сопротивления r вычисляется по формуле)

Ошибка (погрешность) – разность между измеренным и истинным значением.

Систематическая ошибка – ошибка, которая остается постоянной на протяжении всей серии измерений.

Случайная ошибка – ошибка, которая изменяется от опыта к опыту и может быть как положительной, так и отрицательной.

В общем случае результат измерения величины Х представляют в виде:

,

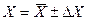где 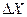погрешность или ошибка измерения; 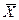- среднее значение величины.

Для однократных измерений за величину ошибки принимается систематическая погрешность, которую вносит сам прибор, а средним считается измеренное значение физической величины.

Измерения длины l проволоки проводится однократно с использованием линейки. Погрешность измерения линейкой определяется как половина цены наименьшего деления.

Измерения величины тока I и напряжения U проводят с помощью электроизмерительных приборов (амперметра и вольтметра). Погрешность DI и DU этих измерений определяется по классу точности, который указан на шкале приборов:

,

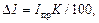
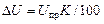где K – класс точности приборов; I_пр и U_пр – наибольшие значения силы тока и напряжения, которые могут быть измерены по шкале прибора.

Диаметр проволоки измеряется многократно штангенциркулем и микрометром. Проведя n измерений, получим серию результатов: 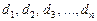. Как величина случайная диаметр варьирует около некоторого среднего значения, которое определяется как среднее арифметическое:

.

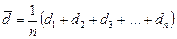Погрешности прямых многократных измерений:

· Среднее значение и средняя абсолютная ошибка.

Предположим, что мы проводим серию измерений величины Х. Из-за наличия случайных ошибок, получаем n различных значений:

Х₁, Х₂, Х₃… Х_n

В качестве результата измерений обычно принимают среднее значение

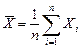(1)

Разность между средним значением и результатом i – го измерения назовем абсолютной ошибкой этого измерения

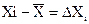
В качестве меры ошибки среднего значения можно принять среднее значение абсолютной ошибки отдельного измерения

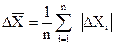(2)

Величина 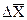называется средней арифметической (или средней абсолютной) ошибкой.

Тогда результат измерений следует записать в виде

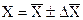
Для характеристики точности измерений служит относительная ошибка, которую принято выражать в процентах

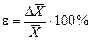(3)

• Средняя квадратическая ошибка.

Если необходимо оценить надежность полученных результатов, как правило вычисляют среднюю квадратическую ошибку (стандартное отклонение):

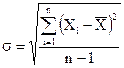(4)

Величина s характеризует отклонение отдельного единичного измерения от истинного значения.

Если мы вычислили по n измерениям среднее значение 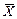по формуле (3), то это значение будет более точным, то есть будет меньше отличаться от истинного, чем каждое отдельное измерение. Средняя квадратичная ошибка среднего значения 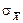равна

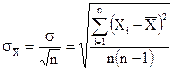(6)

где s - среднеквадратичная ошибка каждого отдельного измерения, n – число измерений.

Таким образом, увеличивая число опытов, можно уменьшить случайную ошибку в величине среднего значения.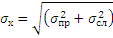

Результаты измерений принято представлять в виде

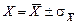
• Учет систематических ошибок.

Увеличением числа измерений можно уменьшить только случайные ошибки опыта, но не систематические.

Максимальное значение систематической ошибки обычно указывается на приборе или в его паспорте. Для измерений с помощью обычной металлической линейки систематическая ошибка составляет не менее 0,5 мм; для измерений штангенциркулем –

0,1 – 0,05 мм; микрометром – 0,01 мм.

Часто в качестве систематической ошибки берется половина цены деления прибора.

На шкалах электроизмерительных приборов указывается класс точности. Зная класс точности К, можно вычислить систематическую ошибку прибора ∆Х по формуле

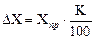
где К – класс точности прибора, Х_пр – предельное значение величины, которое может быть измерено по шкале прибора.

Так, амперметр класса 0,5 со шкалой до 5А измеряет ток с ошибкой не более

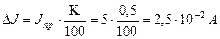
Среднее значение полной погрешности складывается из случайной и систематической погрешностей.

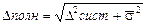
Ответ с учетом систематических и случайных ошибок записывается в виде

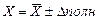
Погрешности косвенных измерений:

В физических экспериментах чаще бывает так, что искомая физическая величина сама на опыте измерена быть не может, а является функцией других величин, измеряемых непосредственно. Например, чтобы определить объём цилиндра, надо измерить диаметр D и высоту h, а затем вычислить объем по формуле

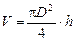
Величины D и h будут измерены с некоторой ошибкой. Следовательно, вычисленная величина V получится также с некоторой ошибкой. Надо уметь выражать погрешность вычисленной величины через погрешности измеренных величин.

Как и при прямых измерениях можно вычислять среднюю абсолютную (среднюю арифметическую) ошибку или среднюю квадратичную ошибку.

Общие правила вычисления ошибок для обоих случаев выводятся с помощью дифференциального исчисления.

Пусть искомая величина φ является функцией нескольких переменных Х, У, Z

φ(Х, У, Z).

Путем прямых измерений мы можем найти величины 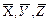, а также оценить их средние абсолютные ошибки 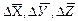или средние квадратичные ошибки s_Х, s_У, s_Z…

Тогда средняя арифметическая погрешность Dj вычисляется по формуле

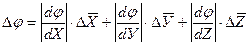
где 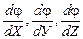- частные производные от φ по Х, У, Z. Они вычисляются для средних значений …

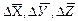Средняя квадратичная погрешность вычисляется по формуле

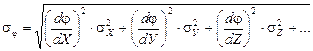
Основные расчетные формулы:

Сопротивление проводника

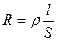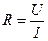, (Ом)

где l –длина проводника (м)

S =πd²/4 – площадь его поперечного сечения (м²),

ρ – удельное сопротивление (Ом*м),

U – напряжение (В),

I – сила тока (А)

Удельное сопротивление

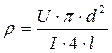(Ом*м)

Среднее значение диаметра проволоки

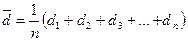, (м)

где n – число измерений

Графическое вычисление

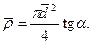(Ом*м)

Формулы погрешностей

При прямых измерениях:

• Величина средней абсолютной ошибки диаметра:

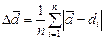, (м)

• Средняя квадратичная ошибка измерений диаметра:

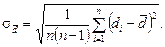(м)

• Абсолютная погрешность прибора:

∆х = х_пр * (К/100),

где х_пр - наибольшее значение на шкале прибора,

К – класс точности прибора

При косвенных измерениях:

· Средняя абсолютная погрешность измерения сопротивления:

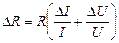,(Ом)

· Средняя квадратическая погрешность измерения сопротивления:

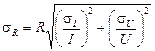, (Ом)

· Средняя абсолютная погрешность измерения удельного сопротивления:

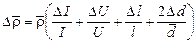, (Ом)

· Средняя квадратическая погрешность измерения удельного сопротивления:

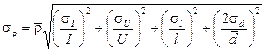, (Ом)

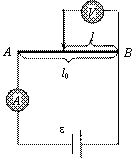
Схема установки:

Для определения удельного сопротивления отрезка проволоки используется простейшая электрическая цепь, которая состоит из источника тока e, амперметра A, вольтметра V и исследуемого проводника АВ (см. рисунок).

Измерения и вычисления

Таблица 1. Результаты измерений диаметра проволоки штангенциркулем и микрометром

Диаметр	Штангенциркуль	Микрометр
Размерность
м	М
d1	0,50*10-3	0,64*10-3
d2	0,45*10-3	0,52*10-3
d3	0,45*10-3	0,49*10-3
d4	0,45*10-3	0,48*10-3
d5	0,50*10-3	0,49*10-3
d6	0,45*10-3	0,52*10-3
d7	0,55*10-3	0,51*10-3
d8	0,45*10-3	0,50*10-3
d9	0,45*10-3	0,50*10-3
d10	0,50*10-3	0,50*10-3
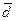	0,48*10-3	0,515*10-3
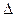đ	15*10-6	1,1*10-6
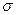d	1,2*10-6	2*10-7
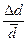	31,2*10-3	2,1*10-3
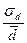	2,6*10-3	4*10-4

Примеры вычислений:

1. Среднее значение диаметра проволоки

Штангенциркуль:

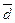= (0,50+0,45+0,45+0,45+0,50+0,45+0,55+0,45+0,45+0,50)/10=0,48*10^-3 (м)

Микрометр:

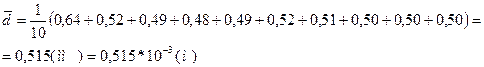
2. Средняя абсолютная погрешность измерения диаметра

Штангенциркуль:

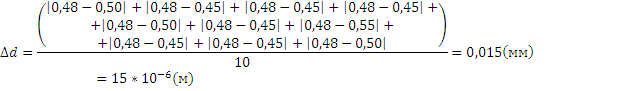
Микрометр:

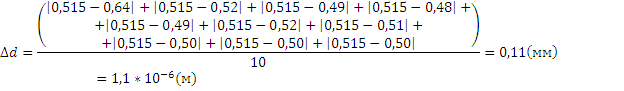
3. Средняя квадратичная погрешность измерения диаметра

Штангенциркуль:

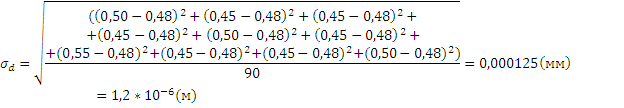
4. Относительная ошибка:

Шангенциркуль:

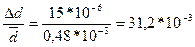
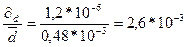
Микрометр:

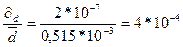
Таблица 2. Результаты измерений тока и напряжения.

Номер опыта		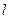		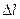		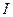	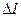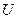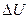R	∆R	σR
	м	м	А	А	В	В	Ом	Ом	Ом
	0,48	5*10-4	0,2	3,75*10-3	0,18	2,25*10-2	0,9	0,36	0,32
	0,43	0,26	1,3	0,26	0,22
	0,38	0,31	1,55	0,23	0,19
	0,28	0,39	1,95	0,19	0,15
	0,23	0,45	2,25	0,17	0,13
	0,18	0,52	2,6	0,16	0,12
	0,13	0,58	2,9	0,14	0,11
	0,08	0,66	3,3	0,13	0,10
	0,03	0,72	3,6	0,13	0,09
	0,005	0,8		0,12	0,08

Примеры вычислений:

1. ∆l – систематическая ошибка металлической линейки : 0,5 мм

2. Погрешность измерений силы тока, напряжения

∆I = (0,25*1,5)/100 = 0,00375(A)

∆U= (1,5*1,5)/100 = 0,0225 (B)

3. Сопротивление

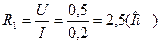
4. Средняя абсолютная погрешность измерения сопротивления

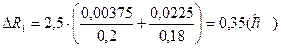
5. Средняя квадратическая погрешность измерения сопротивления

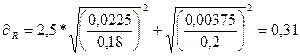(Ом)

График зависимости R = f(l)

Таблица данных для графика:

l, м	0,48	0,43	0,38	0,28	0,23	0,18	0,13	0,08	0,03	0,005
R, Ом	0,9	1,3	1,55	1,95	2,25	2,6	2,9	3,3	3,6

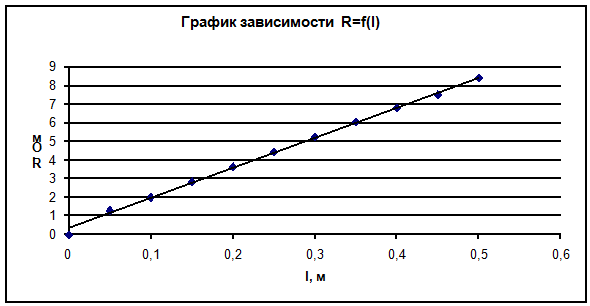
Цена деления по оси l: 0,02; Цена деления по оси R: 0,1

Примеры вычислений:

1. Удельное сопротивление

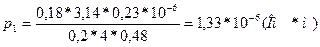
2.Средняя абсолютная погрешность измерения удельного сопротивления

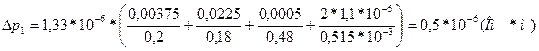
3.Средняя квадратическая погрешность измерения сопротивления