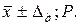Оцінка випадкових похибок прямих вимірювань

Випадкові похибки проявляються при багаторазових спостереженнях вимірюваної величини в однакових умовах одним оператором і за допомогою одного і того ж засобу вимірювання. Такі вимірювання прийнято називати рівноточними.

При статистичній обробці результатів багаторазових спостережень необхідно виконати таку послідовність дій:

1. Провести багаторазові вимірювання і отримати масив Х₁, Х₂, …, Х_n вимірювальної інформації.

2. Поправити результати вимірювань, вилучивши відомі систематичні похибки шляхом внесення поправок у результати спостережень.

3. Знайти математичне сподівання поправлених результатів спостережень і прийняти його за дійсне значення.

Для нормального закону розподілу, а якщо поступитися ефективністю оцінки, то й для всіх симетричних розподілів, за оцінку математичного сподівання ряду рівноточних спостережень приймають середнє арифметичне

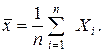
4. Визначити випадкове відхилення.

Різниця 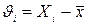представляє собою випадкове відхилення (випадкову абсолютну похибку) при і-му спостереженні. Вона може бути позитивною і негативною.

Середнє арифметичне незалежно від закону розподілу має такі властивост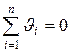і

і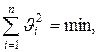

які використовуються для перевірки правильності обчислення .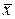

5. Обчислити експериментальне середнє квадратичне відхилення результатів вимірювання за формулою Бесселя

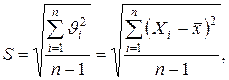
де Х_і – результат і-го вимірювання, 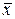- середнє арифметичне n результатів.

Підкреслимо, що для серії n вимірювань однієї й тієї ж величини параметр Sхарактеризує розсіювання результатів багаторазових n вимірювань однієї і тієї ж величини. Оскільки ми обчислюємо середнє арифметичне, необхідне для одержання оцінки σ, то природно взяти його за результат вимірювання. В даному випадку середнє арифметичне залежить від числа вимірювань і є випадковою величиною, яка має деякі дисперсії відносно істинного значення.

6. Середнє квадратичне відхилення середнього арифметичного визначається за формулою

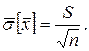
Отже, якщо в якості результату багаторазових вимірювань взяти середнє арифметичне 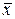, то випадкова похибка (S) зменшується в 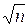разів порівняно з випадком (рис.1), коли за результат багаторазових вимірювань приймалось будь-яке одне з n спостережень. Тому багаторазові вимірювання з наступним усередненням результатів і прийняттям цього середнього за результат вимірювання є досить ефективним методом зменшення випадкової похибки.

7. Визначити довірчі границі похибки вимірювання, що представляє собою верхню й нижню границі інтервалу, який накриває із заданою ймовірністю похибку вимірювання. Якщо число вимірювань n ≤ 20, то довірчий інтервал випадкової похибки при заданих імовірності Р і середньому квадратичному відхиленні 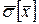визначається за формулою Стьюдента:

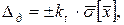
де k_t – коефіцієнт розподілу Стьюдента, який залежить від заданої ймовірності Р і числа вимірювань n.

Розглянемо тепер, яку саме довірчу ймовірність необхідно задавати. Як правило, приймають Р = 0,95. Якщо вимірювання повторити неможливо, то Р = 0,99, а в особливо відповідальних випадках, коли вимірювання, що виконуються, пов’язані із створенням нових еталонів або їхні результати можуть суттєво вплинути на здоров’я людини, Р = 0,997.

8. Представити результат вимірювання