Стандартные электродные потенциалы
Электроды
Перераспределение электронной плотности в окислительно-восстанови-тельной реакции D1 + A2 ® A1 + D2, если проводить ее в специальном устройстве - гальваническом элементе, может быть использовано для создания электродвижущей силы (ЭДС). Рис. 5.1 иллюстрирует, каким образом химическую энергию можно превратить в электрическую.
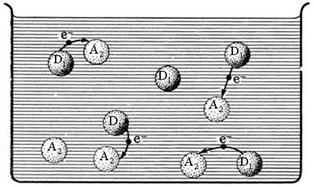 | 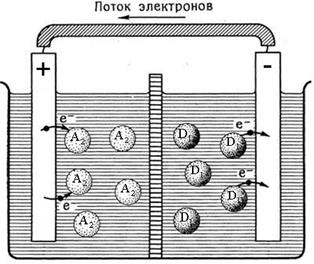 |
Рис. 5.1. Слева – хаотические переходы электронов в массе окислительно-восстанови-тельной реакции; справа – упорядоченные электронные переходы в гальваническом элементе.
Гальванический элемент образован электродами (основная его часть) и может быть дополнен мембраной, проницаемой для одного типа ионов.
Рассмотрим простейший тип электрода металл - ион металла Mz+│M, соответствующий обратимой окислительно-восстановительной полуреакции между ионами металла из раствора и электронами из электрода с образованием нейтральных атомов электрода. Эта гетерогенная реакция протекает на границе раздела фазы раствора (S – solution) и фазы металлического (М - metal) электрода
Mz+ (S) + z e– « M (M) ; Mz+/z + e– « M/z, (5.1)
ze– – избыточная часть «электронного газа» в металле. Подразумевая фазовую принадлежность каждого компонента, чаще используют сокращенную форму записи уравнения полуреакций (вторая в (5.1)).
| В зависимости от природы раствора и металла возможны два варианта. 1) Атомы металла при его растворении покидают кристаллическую решетку и переходят в раствор в виде положительных ионов. За счет оставленных на электроде электронов он приобретает отрицательный заряд и, соответственно, отрицательный потенциал, препятствующий дальнейшему растворению электрода. 2) Ионы осаждаются на электроде. Недостаток электронов, которые нейтрализуют приходящие из раствора ионы, формирует положительный потенциал электрода. | |
| Рис. 5.2. Процессы на электроде. |
Равновесие электрод - раствор и в том, и в другом случае определяется равенством электрохимических потенциалов i-х компонентов в фазе с потенциалом φ. 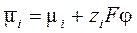 , (5.2)
, (5.2)
где F = 96485.3 Кл/моль – число Фарадея (абсолютная величина заряда моля электронов). Отметим, что электрохимический потенциал, по определению, кроме химического потенциала (μi) включает в себя электростатическую энергию моля частиц с зарядом zi в поле с потенциалом φ.
Итак, для реакции (5.1) на электроде Mz+| M равновесие и соответствующий равновесный потенциал определяются равенством
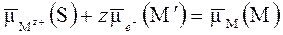 , (5.3)
, (5.3)
где штрих отмечает подфазу электронного “газа” электрода. При подстановке (5.2) в (5.3) получаем
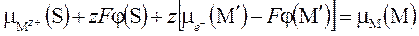 . (5.4)
. (5.4)
Подставляя выраженный через активность химпотенциал катиона в растворе 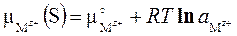 находим межфазную разность потенциалов
находим межфазную разность потенциалов
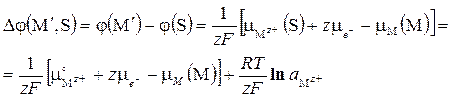 (5.5)
(5.5)
При условии отсчета энергии от состояния простых веществ химический потенциал электрода можно считать равным нулю: 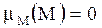 . Введя обозначение для оставшейся части первого слагаемого (5.5)
. Введя обозначение для оставшейся части первого слагаемого (5.5)
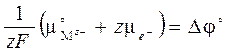 (5.6)
(5.6)
окончательно получаем (штрих, детализирующий фазу М, как и далее – опущен)
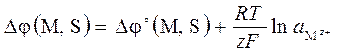 (5.7)
(5.7)
Разность потенциалов на границе раздела фаз электрод (металл) – раствор ионов этого металла (межфазная разность потенциалов) выражена через стандартную разность потенциалов (индекс «˚») и активность (напомним – исправленную концентрацию) ионов в растворе. В свою очередь, стандартное значениеразности потенциалов, выраженное через стандартные химические потенциалы компонентов фаз, как принято, соответствует активности равной 1.
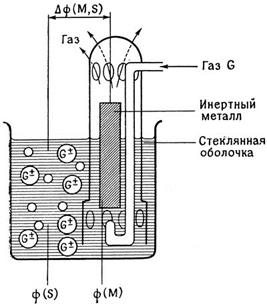
Следующий тип так называемых газовых электродов (рис. 5.3) образован тремя сосуществующими фазами: исходный раствор, газ, обе эти фазы контактируют с фазой инертного металла. Обозначение электрода: G± | G2 | Pt (если инертный металл - платина).
Вариант (а) 1/2 G2 + e– « G–, например G– ≡ Cl– – ионы хлора в растворе;
Вариант (б) G+ + e– « 1/2 G2, например G+ ≡ H+ .
 | Условие равновесия для приэлектродной химической реакции (вариант (а)), как и ранее определяется соответствующим уравнением для электрохимических потенциалов: 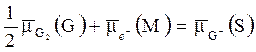 . (5.8) . (5.8) 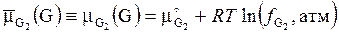 , , 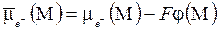 , , 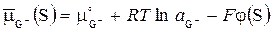 . Первый из входящих в (5.8) электрохимических потенциалов для не заряженного газового компонента равен химическому потенциалу. . Первый из входящих в (5.8) электрохимических потенциалов для не заряженного газового компонента равен химическому потенциалу. |
| Рис. 5.3. Электрод газ |инертный металл. |
При этом в отличие от идеального химический потенциал неидеального газа, выражается не через давление, а через летучесть f, аналогично активности соответствующей исправленному давлению.
В полученной после аналогичных преобразований разности потенциалов уравнению (а) соответствует верхний знак, уравнению (б) - нижний:
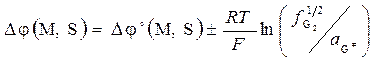 , (5.9)
, (5.9)
где 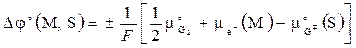 – стандартное значение межфазного потенциала при f и a = 1.
– стандартное значение межфазного потенциала при f и a = 1.
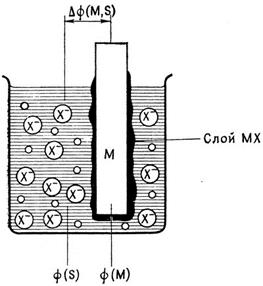 | Электрод - ион | нерастворимая соль | металл (X– | MX | M) имеет две поверхности раздела. С одной стороны соль MX контактирует с раствором, содержащим анионы X–, а с другой стороны - с металлом M. Обычный пример - хлорсеребряный электрод: Cl– | AgCl | Ag . Еще один пример такого электрода - так называемый каломельный электрод Cl– | Hg2Cl2 | Hg . Электродная реакция MX + e‾ ↔ M + X‾ включает компоненты трех фаз, что учитывается при записи условия равновесия (5.10): |
| Рис. 5.4. Электрод ион | нерастворимая соль | металл |
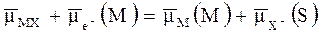 , (5.10)
, (5.10)
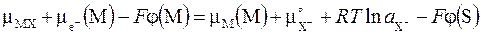 ,
,
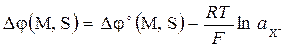 , (5.11)
, (5.11)
где 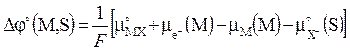 . (5.12)
. (5.12)
Все рассмотренные выше электроды - материализация окислительно-восстановительных или редокс-реакций, связанных с переносом электронов. Однако термин редокс-электрод применяется в тех случаях, когда вещества в растворе существуют в двух окислительных состояниях.
Обозначение редокс-электрода A2+, A+ | M , где M - инертный металл соответствует полуреакции A2+ + e– = A+.
Примеры: Fe3+ + e– « Fe2+ - биологически важное гидрохиноновое равновесие.
Вывод, подобный предыдущим, дает выражение для межфазной разности потенциалов и его стандартной составляющей
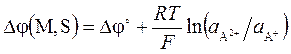 , (5.13)
, (5.13)
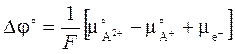 . (5.14)
. (5.14)
Важно, что положение равновесия с необходимым соотношением окисленных форм можно регулировать изменением разности потенциалов. С другой стороны раствор с заданным соотношением концентраций восстановленных и окисленных ионов позволяет поддерживать требуемую разность потенциалов.
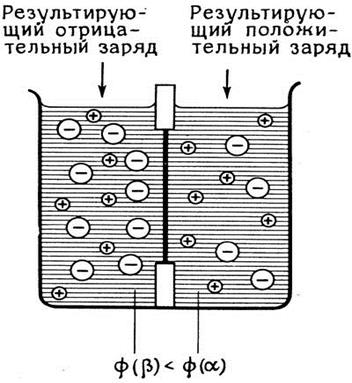 | Если два раствора соли MX различной концентрации разделить мембраной, проницаемой, например, только для катионов M+, то за счет их диффузии в разбавленный раствор устанавливается мембранный потенциал: 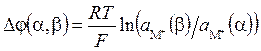 – следствие равенства электрохимических потенциалов фаз α и β с различной концентрацией ионов. Один из "живых" примеров мембранной системы - стенка биологической клетки, – следствие равенства электрохимических потенциалов фаз α и β с различной концентрацией ионов. Один из "живых" примеров мембранной системы - стенка биологической клетки, |
| Рис. 5.5. Возникновение мембранного потенциала. |
которая более проницаема для ионов K+, чем для Na+ и Cl¯. Внутри клетки концентрация K+ в 10‑30 раз больше, чем снаружи и поддерживается действием "специального насоса". Горючее для него –аденозинтрифосфорная кислота (АТФ). Управление ферментами. Dj(in,ex) = 0,07 В.
Импульс 0,02 В изменяет структуру мембраны, и она становится проницаемой для Na+. Это приводит к уменьшению Dj(in,ex) , которое в свою очередь приводит в активность соседние клетки и т.д., что формирует волну передачи нервных импульсов.
Гальванические элементы
Комбинация двух электродов образует гальванический элемент или гальваническую ячейку.
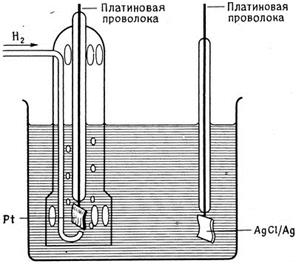 | 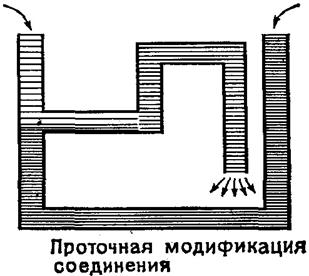 |
| Рис. 5.6. Гальванический элемент без жидкостного соединения. | Рис. 5.7 а. Проточный вариант жидкостного соединения. |
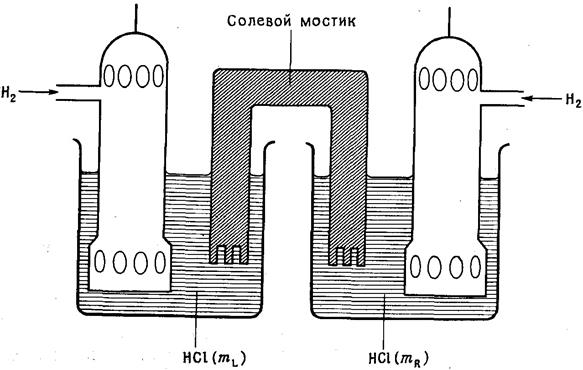 Рис. 5.7 б.Солевой мостик. Рис. 5.7 б.Солевой мостик. |
Например, сочетание водородного и хлорсеребряного электродов дает наиболее простой элемент без жидкостного соединения, т.е. элемент с общим электролитом (рис. 5.6).
Pt, H2 | HCl | AgCl, Ag, Pt
Если два электрода, левый (L) и правый (R), помещены в два разных электролита, то образуется элемент с жидкостным соединением.
Варианты жидкостного соединения для так называемого концентрационного элемента (электролиты у левого и правого электродов отличаются только концентрацией, в данном случае в единицах моляльности) показаны на рис. 5.7.
Pt, H2 | HCl(mL) | HCl(mR) |H2, Ag, Pt
Другим способом жидкостного соединения полуэлементов является так называемый солевой мостик (рис. 5.7), приготовленный растворением KCl в водорастворимом желе. Ток в мостике определяется высокой концентрацией переносимых ионов K+ и Cl¯. Считается, что дополнительные потенциалы "солевой мостик" ‑ раствор взаимно сокращаются. Причины и механизм успешного действия солевого мостика к настоящему времени до конца не выяснены.
Диффузионные контакты двух растворов посредством жидкостного соединения вносят элементы неравновесности, осложняющие термодинамический анализ.
Жидкостное соединение можно исключить, сконструировав двойной элемент (два одинаковых элемента - навстречу).
Pt, H2 | HCl(mL)|AgCl, Ag...Ag, AgCl | HCl(mR) | H2, Pt
Такое исключение жидкостного соединения между полуэлементами в формуле элемента обозначается значком ||.
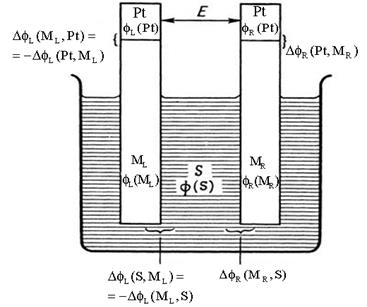 | Разность потенциалов гальванического элемента, измеренная при равновесии (ток не протекает) и между платиновыми клеммами, называется электродвижущей силой (ЭДС). Кроме аббревиатуры используют обозначения э.д.с. или E. Математическая аддитивность потенциалов определяет результирующую разность потенциалов как сумму межфазных. |
| Рис. 5.8. Определение э.д.с. элемента по разностям потенциалов. |
Производя суммирование, начиная с правой платиновой клеммы, получаем:
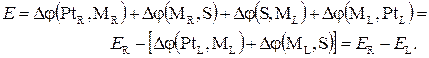 (5.15)
(5.15)
1) Э.д.с. выражается в виде разности электродных потенциалов (5.16), которые кроме собственно межфазной разности потенциалов, включают контактную разность потенциала платиновой клеммы, если электрод не платиновый.
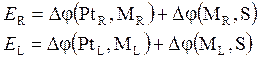 (5.16)
(5.16)
Отметим, что обозначения в скобках совмещают и названия веществ электродов, раствора и их агрегатное состояние.
2) Принимается соглашение (обязательное для последующего изложения): знак э.д.с. всегда относится к разности потенциалов ER– EL правого и
левого электродов в том виде, в которомзаписан гальванический элемент (при желательной, но не обязательно аналогичной схеме его монтажа на подставке).
| Общая запись Pt | ML | S | MR | Pt | : | Пример Pt | H2( 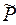 ) | HCl(m) |AgCl, Ag | Pt ) | HCl(m) |AgCl, Ag | Pt | ||
| L | R | L | R | |
Примечания. Напомним, что межфазная граница в обозначении гальванического элемента, как правило, отмечается вертикальной чертой. Иногда внутреннюю межфазную границу, как в записи хлорсеребряного электрода, отмечают запятой. Запятой может быть отмечена и контактная платиновая клемма. Дополнительно в скобках конкретизируется: 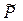 , в единицах атм., давление для газового электрода, а для раствора – концентрация, обычно в моляльностях m.
, в единицах атм., давление для газового электрода, а для раствора – концентрация, обычно в моляльностях m.
Максимально положительная ЭДС будет наблюдаться в том случае, если потребляющая электроны восстановительная реакция 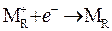 , создающая их дефицит и положительный потенциал на правом электроде, сочетается с окислительным высвобождением электронов
, создающая их дефицит и положительный потенциал на правом электроде, сочетается с окислительным высвобождением электронов 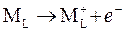 , дающим отрицательный потенциал на левом электроде.
, дающим отрицательный потенциал на левом электроде.
Сложение протекающих слева направо полуреакций естественно даст реакцию того же направления и соответственно положительную ЭДС.
E > 0, 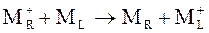 . (5.17+)
. (5.17+)
Обратное протекание указанных процессов даёт отрицательную ЭДС
E < 0, 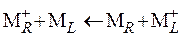 . (5.17¯)
. (5.17¯)
Правило определения направления спонтанной ОВР L + R+ = L+ + R по э.д.с.соответствующегогальваническогоэлемента L | L+ | R+ | R при использовании потенциалов восстановительных полуреакций.(Веществам правого и левого электродов соответствуют символы R и L.):
1. Записываем полуреакции на электродах в восстановительной форме с табличными значениями потенциалов (две первые строки). При этом к правому электроду относится та из них, которая по направлению совпадает с направлением анализируемой ОВР (вторая строка). Относимая к левому электроду сопряженная окислительная полуреакция, исходя из записанной восстановительной её формы, читается справа налево.
2. Для получения анализируемой реакции (третья и четвертая строки слева) производим вычитание реагентов и продуктов полуреакции левого электрода из полуреакции правого, а также соответствующее вычитание потенциалов для получения э.д.с. (третья строка справа).
3. Реакция протекает в направлении, указываемом знаком э.д.с. (четвертая строка справа).
| – | L+ + e– = L | EL |
| R+ + e– = R | ER | |
| R+ – L+ = R – L | E = ER - EL | |
| R+ + L = R + L+ | E > 0 – вправо; E < 0 – влево. |
Более наглядный способ реализации правила(с использованием ранее введенного значка сопряжения полуреакций) предусматривает при записи суммарной реакции сложение реагентов по «хвостам» стрелок и продуктов - по «остриям».
| + | L+ + e– R+ + e– | 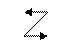 | L EL R ER |
| L + R+ = L++ R E = ER - EL |
Пример - реакция коррозии железа в кислотных условиях
Fe + 2 H+Cl¯ (aq) + 1/2 O2 = Fe2+Cl¯2(aq) + H2O
L: 1/2 Fe2+ + e– ← 1/2 Fe -0,44 В
R: H+ + e– + 1/4 O2 → 1/2 H2O 1,229 В
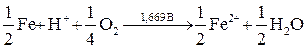 E = 1,229 – (-0,44) =1,669 В
E = 1,229 – (-0,44) =1,669 В
Положительная и значительная по величине ЭДС подтверждает активную роль этой реакции в коррозии железа.
Уравнение Нернста
Рассмотрим элемент L | L+ || R+ | R, в котором идет реакция L + R+ = L+ + R. Его э.д.с., ранее выраженная через разность электродных потенциалов (5.16), при последующей подстановке в них межфазных потенциалов (5.7) приводит к уравнению Нернста (5.18).
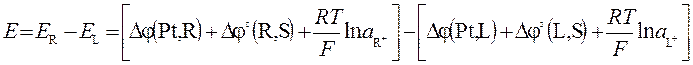
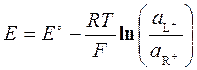 , (5.18)
, (5.18)
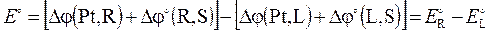 . (5.19)
. (5.19)
Это важное для практических приложений уравнение определяет концентрационную зависимость э.д.с. электрохимического элемента относительно стандартной э.д.с. (5.19), соответствующей концентрациям, точнее активностям компонентов в электролите ai = 1.
Стандартные электродные потенциалы
Потенциал одного электрода не входит в термодинамические выражения для параметров, которые могут быть измерены на практике.
Поскольку имеет смысл говорить только о разности потенциалов, то одному электроду можно придать нулевое значение, и все другие электроды относить к нему. В качестве электрода с нулевым потенциалом выбирают стандартный водородный электрод (СВЭ). Его стандартный потенциал достигается, когда активность ионов водорода равна единице; давление газообразного водорода, точнее его летучесть равна 1 атм, а температура составляет 298,15 К (25 °С).
СВЭ: H+( 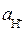 =1) | H2( f =1 атм), Pt ; E°(H+ | H2) º 0. (5.20)
=1) | H2( f =1 атм), Pt ; E°(H+ | H2) º 0. (5.20)
Стандартный потенциал других электродов может быть получен путем формирования гальванического элемента, в котором СВЭ находится слева, а исследуемый - справа. Ионы и газы исследуемого электрода приводятся к единичной активности и тогда E°(элемента) = E°R – E°(СВЭ) = E°R
К настоящему времени существуют таблицы стандартных электродных потенциалов. Причем современные их формы содержат стандартные потенциалы восстановления, соответствующие восстановительной форме записи электродной полуреакции. И, тем не менее, для контроля следует запомнить, что в такой таблице медь имеет положительный потенциал.
Cu+ + e– = Cu , E°(Cu+ | Cu) = 0,521 В
Метод определения направления протекания реакций по электродным потенциалам восстановления - мощный количественный инструмент анализа окислительно-восстановительных реакций, учитывающий при необходимости концентрационные соотношения компонентов в растворе.
Пример: Можно ли анодным растворением (окислением) Zn вытеснить (восстановить) из раствора ионы 1) Cu2+, 2) Mg2+ ?
А: 1/2 Zn2+ + e– ↔ 1/2 Zn; E° = ‑0,763 В
К: 1) 1/2 Cu2+ + e– → 1/2 Cu; ∆E° = 0,337 - (‑0,763) > 0 – да.
2) 1/2 Mg2+ + e– ← 1/2 Mg; ∆E° = -2,37 - (‑0,763) < 0 – нет.
Металлы, расположенные в порядке возрастания их стандартных восстановительных потенциалов образуют так называемый электрохимический ряд напряжений металлов: Li, Rb, K, … Mg, Al, Mn, Zn, … H, … Cu, … Pt, Au.
·Каждый металл способен вытеснять (восстанавливать) из растворов солей те металлы, которые стоят в ряду напряжений после него.
·Все металлы левее водорода, т.е. имеющие отрицательный потенциал, способны вытеснить водород из растворов кислот.
Процедура определения стандартных электродных потенциалов, рассмотренная на примере хлорсеребряного электрода, состоит в измерении э.д.с. элемента Pt, H2 (1 атм) | HCl(m) | AgCl | Ag, Pt. Его э.д.с., равная разности (5.15) правого и левого электродных потенциалов (5.16) с учетом межфазных разностей потенциалов (5.11) в приложении к хлорсеребряному электроду и ((5.9), вариант б)) к водородному при соглашении (5.20), принимает вид:
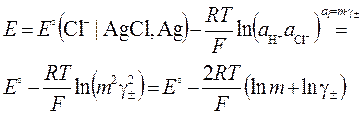 (5.21)
(5.21)
Напомним, что по теории Дебая-Хюккеля среднеионный коэффициент активности для разбавленных растворов 1:1 определен формулой 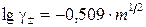 , где m - моляльность.
, где m - моляльность.
Экспериментально исследуя зависимость E(m) в области разбавленного раствора, методом математической обработки находят ее предельное (m → 0) значение E°. После этого можно экспериментально определить зависимость g± от m в более широкой области концентраций.
