Направление самопроизвольного протекания химических реакций
I закон термодинамики устанавливает взаимосвязь между внутренней энергией, теплотой и работой и позволяет рассчитывать тепловые эффекты различных процессов, но при этом обладает одним существенным недостатком: он ничего не говорит о направлении самопроизвольного протекания процесса. Действительно, с точки зрения I закона термодинамики барон Мюнхгаузен, пытаясь вытащить себя и лошадь из болота за косичку, затратив некоторое количество энергии, не сделал ничего предосудительного. Можно привести и другой пример. Процесс нагревания-охлаждения воды является обратимым. Воду в чайнике можно довести до кипения при помощи электрического тока, однако при остывании воды ток в цепи не возникает.
Почему?[6]
Ответ даёт II закон термодинамики.
Любой самопроизвольно протекающий процесс (химическая реакция) реализуется как результат соотношения двух основных тенденций:
1) стремление системы свести к минимумусвой запас внутренней энергии, выделить избыток этой энергии в окружающую среду – принцип Бертло-Томсена;
2) стремление системы перейти в наиболее вероятное, т.е. наиболее устойчивое состояние, характеризующееся максимальной степенью беспорядка, хаотичности.
1-я тенденция учитывает энтальпийный фактор и проявляется в том, что большинство самопроизвольно протекающих реакций имеет экзотермический характер, DHр-я < 0.
2-я тенденция учитывает энтропийный фактор, ΔS > 0.
Энтропия S – функция состояния системы, определяющая её термодинамическую вероятность и в этом смысле устойчивостьданного состояния.
Физический смысл энтропии установила статистическая термодинамика. Согласно уравнению Больцмана:
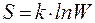 , | (9) |
где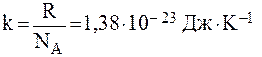 
- постоянная Больцмана, R – универсальная газовая постоянная, NA – число Авогадро; W - число способов, которыми система может осуществить свое макросостояние, или, другими словами, это термодинамическая вероятность данного макросостояния системы, которая определяется числом способов и вариантов распределения микрочастиц (молекул, атомов, ионов и т.д.).
Статистическая трактовка понятия энтропии означает, что в отличие от энергии, которая присуща каждой отдельной частице, энтропия отражает свойства набора частиц. Отдельная частица энтропией не обладает.
Таким образом, энтропия характеризует неупорядоченность, вероятность существования системы и является таким же свойством вещества или системы, зависящим от их природы и состояния, как температура, давление, внутренняя энергия и энтальпия.
Как и для других термодинамических функций состояния, в расчётах используют стандартные значения энтропии S (Дж/K) и S0 (Дж/моль×K).
Как и энергия, энтропия не относится к числу экспериментально определяемых величин. В обратимом процессе, протекающем в изотермических условиях, изменение энтропии равно:
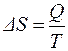 . | (10) |
В необратимых процессах выполняется неравенство:
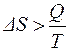 . | (11) |
Это означает, что при необратимом протекании процесса энтропия возрастает благодаря переходу части работы в теплоту.
Таким образом, в обратимых процессах система совершает максимально возможную работу. При необратимом процессе система всегда совершает меньшую работу.
Переход работы в теплоту в необратимом процессе означает переход от упорядоченной формы материи к неупорядоченной. Отсюда и возникает трактовка энтропии как меры беспорядка в системе:
При увеличении беспорядка в системе энтропия возрастает и, наоборот, при упорядочивании системы энтропия уменьшается.
Внеобратимыхпроцессах, сопровождающихся увеличением S, энтропия производится (возникает), это происходит, например, при выравнивании концентраций.
Энтропия закрытой системы может изменяться и при обмене системы с окружающей средой теплотой, т.е. только энергией.
Изменение энтропии в результате теплообмена называется потоком энтропиии определяется уравнением:
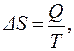где Q ‑ теплота, которой обменивается система с внешней средой при температуре Т.
Общее изменение энтропиисистемыопределяется суммой производимой энтропии(в необратимом процессе) и потока энтропии(приобретаемой или выделяемой в результате теплообмена). В обратимых процессах энтропия не производится и всё её изменение определяется только потоком энтропии.
Большинство протекающих в природе процессов является необратимыми и сопровождаются производством энтропии.
В процессе испарения воды энтропия увеличивается, в процессе кристаллизации - уменьшается. В реакциях разложения энтропия увеличивается, в реакциях соединения - уменьшается.
Если обратимый процесс протекает в изобарно-изотермических условиях, то должны выполняться следующие соотношения:
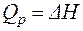 | (12) |
и
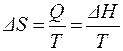 , | (13) |
Таким образом, в обратимом процессе:
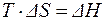 . | (14) |
В необратимом процессе выполняется неравенство:
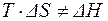 . | (15) |
От соотношения величин, стоящих в левой и правой части последнего выражения, зависит направление самопроизвольного протекания процесса.
Если процесс проходит в изобарно-изотермических условиях, то общая движущая сила процесса называется свободной энергией Гиббса или изобарно-изотермическим потенциалом (DG):
Уравнение Гиббса:
ΔG = ΔH – T×ΔS(16)
Энтальпийный энтропийный
Фактор фактор
Энергия Гиббса измеряется в Дж или в кДж.
Знак DG позволяет определить направление самопроизвольного протекания процесса:
Если DG < 0, то процесс в принципе осуществим, в данных условиях он теоретически может идти самопроизвольно, а абсолютное значение разности ΔН ‑ ТΔS определяет движущую силу этого процесса.
Если DG > 0, то в данных условиях реакция самопроизвольно протекать не может, и осуществима обратная реакция, для которой ΔG < 0.
Если DG = 0, реакция обратима, это критерий состояния химического равновесия.
Анализ соотношения энтальпийного и энтропийного факторов в уравнении (16) позволяет сделать следующие заключения:
1. При низких температурах преобладает энтальпийный фактор, и самопроизвольно протекают, в основном, экзотермические процессы;
2. При высоких температурах решающую роль играетэнтропийный член уравнения, возрастающий в реакциях разложения. Поэтому при достаточно больших температурах не могут существовать сложные системы.
Предложенный подход позволяет целенаправленно подбирать условия, при которых процесс протекает в заданном направлении.
Как правило, итогом процесса является результат суммарного действия двух рассмотренных факторов. Например, распределение атмосферного газа происходит под действием энтальпийного фактора ΔН < 0 (стремление распределиться по поверхности Земли) и энтропийного фактора ΔS > 0 (стремление рассеяться в космическом пространстве).
На основании изложенного материала можно сформулировать II закон (начало) термодинамики: