Методика обработки результатов опыта
6.3.1 Построение седиментационной кривой 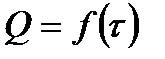
Таблица 6.1 – Данные для расчета седиментационной кривой
Время 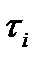 , с , с | Масса пустой чашки m0, мг | Показания торсионных весов mi, мг | 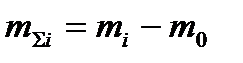 | 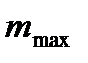 | Q, % | h, м | 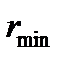 , м , м | 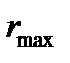 , м , м |
Расчетные формулы:
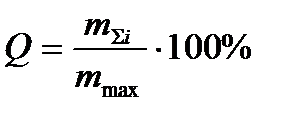 ;
;
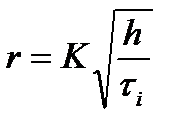 ;
;
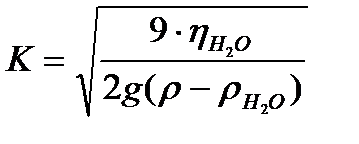 ,
,
где 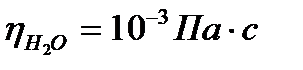 ;
;
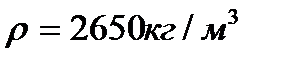
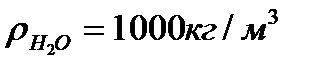 ;
;
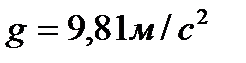
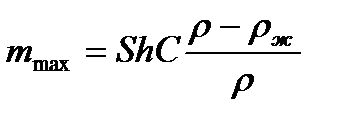
где S – площадь чашки весов;
h – высота столба суспензии;
С – концентрация вещества дисперсной фазы, мг/м3.
Если все величины измеряются в единицах системы СИ, то масса будет измеряться в мг.
| Q, % |
| Q3 % |
| Q2 % |
| Q1 % |
| t, c |
| tmax |
| tmin t1 t2 t3 |
Рисунок 6.3 – Построение седиментационной кривой
6.3.2 Построение интегральной кривой распределения 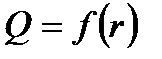
Таблица 6.2 – Данные для расчета интегральной кривой распределения
Время 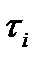 , с , с | 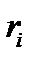 , м , м | Qi, % |
Расчетные формулы:
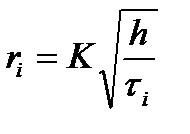 ;
;
Qi, % определяется из графика на рисунке 6.3.
| Q, % ΔQ2 ΔQ1 |
| r3 r2 r1 |
| Δr2 |
| Δr1 |
| r, м |
Рисунок 6.4 – Построение интегральной кривой распределения
6.3.3 Построение дифференциальной кривой распределения 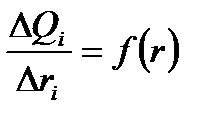
Таблица 6.3 – Данные для расчета дифференциальной кривой распределения
| Qi, % | 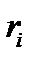 , м , м | 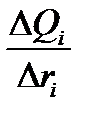 | 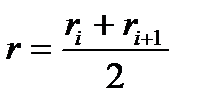 |
Значения 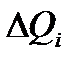 и
и 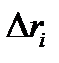 определяются на основании графика на рисунке 6.4. Расчетные формулы:
определяются на основании графика на рисунке 6.4. Расчетные формулы:
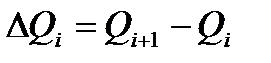
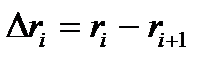
| r, м |
| rmin rвер rmax |
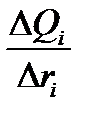 |
Рисунок 6.5 – Построение дифференциальной кривой распределения
Форма отчета
Отчет должен содержать название и цель работы, краткий конспект теоретической части и методики проведения опыта, заполненные таблицы со всеми промежуточными расчетами и краткими пояснениями, графики зависимостей 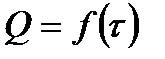 ;
; 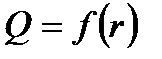 ;
; 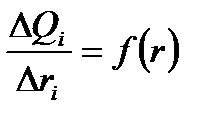 ; выводы о характере дисперсности изучаемой системы и о ее фракционном составе.
; выводы о характере дисперсности изучаемой системы и о ее фракционном составе.
Примеры решения задач
Пример 1
Дисперсность сферических частиц составляет 0,8·106 м-1. Плотность дисперсной фазы и дисперсионной среды равны соответственно 2,1 и 1,1 г/см3. Вязкость дисперсионной среды составляет 2·10-3Па·с. Рассчитайте время, за которое частицы осядут на 0,1м.
Решение
Дисперсность частиц правильной формы представляет собой величину, обратную главному линейному размеру частиц. Для сферических частиц дисперсность – величина обратная диаметру, то есть
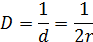
Скорость оседания частиц с радиусом r при соблюдении закона Стокса выражается уравнением
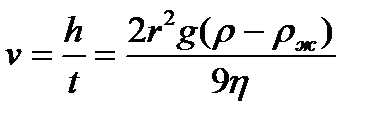 ,
,
откуда выражается и рассчитывается время оседания:
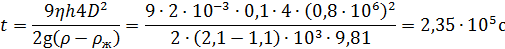
6.5 Требования к уровню подготовки студентов
¾ Знать теоретические основы и методику проведения седиментационного анализа.
¾ Уметь по результатам опыта строить интегральные и дифференциальные кривые распределения частиц по размерам, на их основе делать выводы о характере дисперсности изучаемой системы и ее фракционном составе.
6.6 Задания для самоконтроля
6.6.1 Запишите формулу для расчета скорости седиментации в гравитационном поле. Каков физический смысл входящих в него величин? Изменение каких параметров системы приводит к увеличению скорости осаждения частиц?
6.6.2 Каковы условия соблюдения закона Стокса при седиментационном анализе? К каким ошибкам приводит несоблюдение этих условий?
6.6.3 Что характеризует константа седиментации? Запишите формулу для ее расчета в условиях соблюдения закона Стокса для частиц сферической формы.
6.6.4 Что такое монодисперсные и полидисперсные системы? В чем заключаются различия в форме седиментационных кривых для этих систем?
6.6.5 Для чего используются интегральные и дифференциальные кривые распределения частиц по размерам? Как будет изменяться вид этих кривых при переходе от полидисперсных систем к монодисперсным?
6.6.6 Как определяется содержание частиц данной фракции по интегральным и дифференциальным кривым распределения?
6.6.7 Время оседания сферических частиц на 1 см составляем 30 мин. Плотность дисперсной фазы и дисперсионной среды равны соответственно 2 и 1 г/см3. Вязкость дисперсионной среды составляет 1,5·10-3Па·с. Рассчитайте размер частиц дисперсной фазы.
6.6.8 Дисперсность сферических частиц составляет 105 м-1. Плотность дисперсной фазы и дисперсионной среды равны соответственно 2,2 и 1 г/см3. Вязкость дисперсионной среды составляет 10-3Па·с. Рассчитайте время, за которое частицы осядут на 1см.
Лабораторная работа №7
