Закон ома в дифференциальной форме

Немецкий физик Г. Ом (1787 – 1854) экспериментально установил, что сила тока на участке, не содержащем ЭДС прямо пропорциональна напряжению:

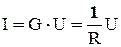, (11)

где коэффициент пропорциональности G = 1 / R и называется электрической проводимостью проводника. Для линейных проводников с постоянным поперечным сечением

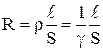, (12)

где γ = 1 / ρ – удельная электропроводность материала, ρ – удельное сопротивление,S – площадь поперечного сечения проводника, 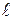– его длина. Тогда для изотропного проводника выражение (11) с учётом (12) примет вид:

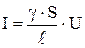. (13)

Теперь для плотности тока (2) с учётом, что 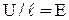– напряжённость поля в проводнике, получим:

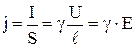. (14)

Выражение (14) в векторной форме это закон Ома в дифференциальной форме:

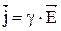. (15)

Получим в дифференциальной форме закон Джоуля-Ленца. Количество теплоты, выделяющееся в элементе проводника, объёмом 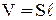за время dt:

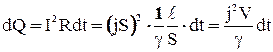. (16)

Теперь, количество теплоты, которое выделяется в единице объема проводника за единицу времени, будет:

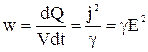. (17)

Эта величина называется удельной тепловой мощностью тока.