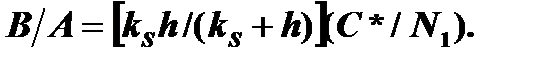Модель термического окисления

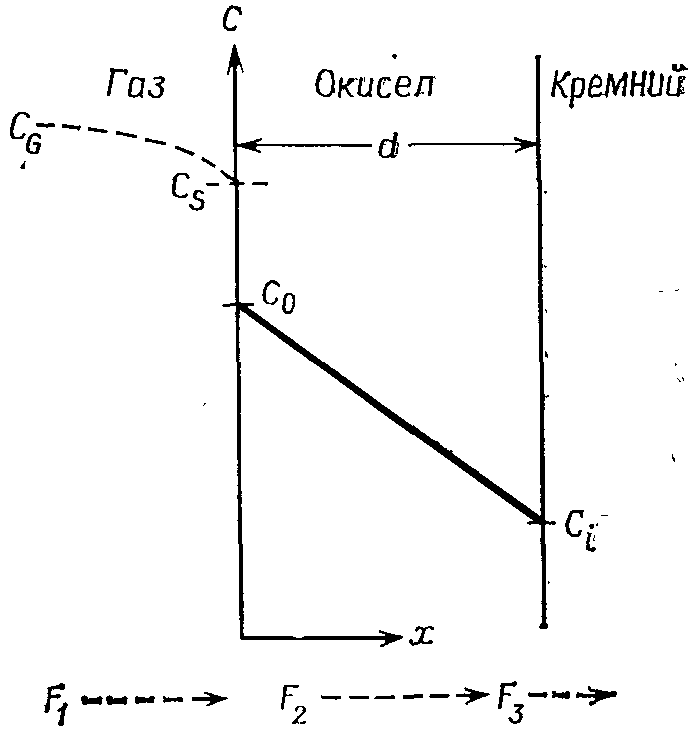Окисляющие элементы диффундируют из объёма газовой среды на границу раздела газ – окисел (поток F₁), переносятся через уже образованный окисел по направлению к кремнию (поток F₂)

и реагируют на границе раздела фаз Si-SiO₂ с кремнием (поток F₃). C_G – концентрация окислителя в объёме газовой фазы; С_S – вблизи поверхности окисла; С₀ – равновесная концентрация в окисле на внешней стороне; С_i – вблизи границы раздела фаз.

Уравнение для потока F₁

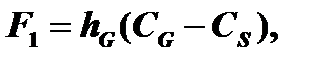Поток F₁ пропорционален разности концентраций окислителя:

где h_G – коэффициент массопереноса в газовой фазе.

Согласно закону Генри:

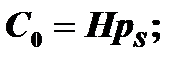
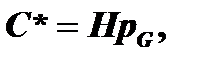
где С*-равновесная объёмная концентрация в окисле, p_S –парциальное давление в газовой фазе вблизи поверхности окисла, p_G – парциальное давление в объёме газовой фазы, Н – постоянная Генри.

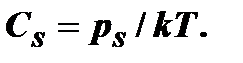
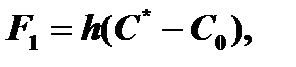
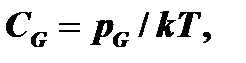При использовании закона Генри совместно с законом идеальных газов:

где h – коэффициент массопереноса в газовой фазе, определяемый как:

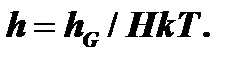
Уравнение для потока F₂

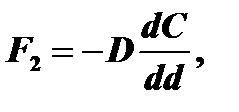Поток частиц окислителя через окисел для любой точки d описывается законом Фика:

где D – коэффициент диффузии, dC/dd – градиент концентрации частиц окислителя в окисле.

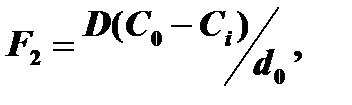При установившемся процессе поток F₂ одинаков для любой точки окисла (dF₂/dd=0):

где d₀ – толщина окисла.

Уравнение для потока F₃

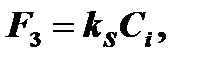
Поток, соответствующий реакции, пропорционален C_i:

где k_S – константа скорости химической реакции окисления кремния.

Решение уравнений для С_i и С₀

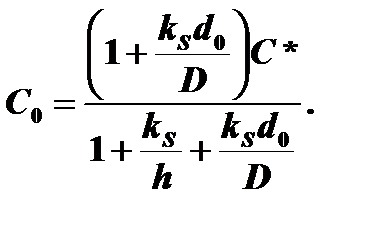
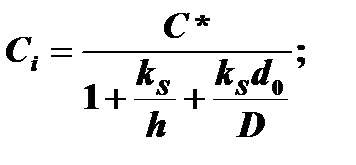Для установившегося потока соблюдается условие F₁=F₂=F₃. Тогда совместное решение уравнений

даёт следующие выражения для С_i и С₀:

Предельные случаи уравнений для С_i и С₀

1. Если D слишком мал, то С_i→0, C₀→C*,

т.е. реакция идет при диффузионном контроле.

2. Если D слишком велик, то реакция идет при кинетическом контроле: С_i=C₀→C*/(1+k_Sh).

Определение числа молекул окислителя, входящих в состав SiO₂

Окисел содержит 2,2×10²² молекул SiO₂ в 1 см³. На создание одной молекулы SiO₂ требуется одна молекула O₂ или 2 молекулы H₂O.

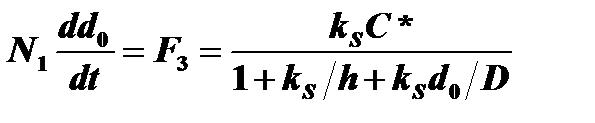Таким образом число молекул окислителя,входящих в 1 см³ окисла (N₁) составляет:-,4×10²² для окисления в парах воды. 2,2×10²² для окисления в сухом кислороде

Тогд4а:

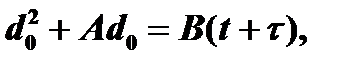Зависимость толщины отвремени процесса

(*)

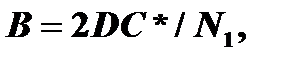
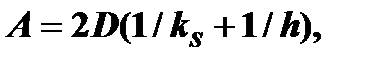
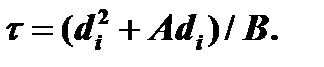где:

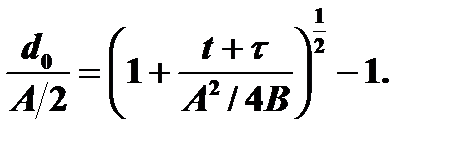Величина τ соответствует сдвигу по временной оси, учитывающему наличие первоначального слоя окисла толщиной d_i.

Тогда решение (*) имеет вид:

Предельные случаи решения уравнения для толщины окисла

1. 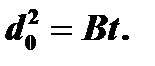Большое время окисления (t>>τ):

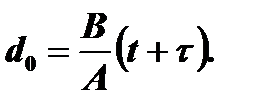Уравнение представляет собой параболический закон, В – параболическая константа скорости окисления.

2. Малое время окисления (t+τ)<<A²/4B:

Уравнение представляет собой линейный закон,

В/А – линейная константа скорости окисления: