Энергетика химических процессов. Термодинамические величины

Химическая термодинамика - позволяет рассчитать тепловые эффекты реакции, определить принципиальную возможность и направленность протекания данной реакции, определить условия, при которых возможно протекание данной реакции.

Термодинамическая система - это тело или группа тел, находящихся во взаимодействии друг с другом, или же совокупность всех химических реагентов, находящихся в определенном объеме пространства.

Термодинамические системы могут быть изолированными и неизолированными.

Изолированной называется система, которая не обменивается с окружающей средой ни веществом, ни энергией.

Неизолированная - система, обменивающаяся с окружающей средой теплом или энергией.

Система может быть гомогенной и гетерогенной (рис. 12).

Гомогенной называется такая система, в которой нет поверхности раздела между составляющими ее компонентами.

Гетерогенной называется система, в которой отдельные компоненты разделены поверхностями раздела.

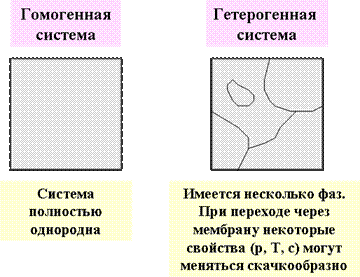Рисунок 12. Классификация термодинамических систем по фазовому составу

Состояние любой термодинамической системы может быть охарактеризовано количественно с помощью термодинамических переменных. Все они взаимосвязаны, и для удобства построения математического аппарата их условно делят на независимые переменные и термодинамические функции. Переменные, которые фиксированы условиями существования системы, и, следовательно, не могут изменяться в пределах рассматриваемой задачи, называют термодинамическими параметрами. Различают переменные:

· внутренние, которые зависят только от свойств самой системы, например, плотность ρ, внутренняя энергия U; в отличие от внешних переменных, число таких свойств неограниченно;

• внешние, которые определяются свойствами и координатами тел в окружающей среде и зависят от контактов системы с окружением, например, массы или количества компонентов ν, напряженность электрического поля Е; число таких переменных ограниченно;
• экстенсивные, которые прямо пропорциональны массе системы или числу частиц, например, объем V, внутренняя энергия U, энтропия S, теплоемкость C;
• интенсивные, которые не зависят от массы системы или числа частиц, например, температура T, плотность ρ, давление Р. Отношение любых двух экстенсивных переменных является интенсивным параметром, например парциальный мольный объем 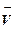или молярная доля Х.

Состояние системы описывается также с помощью термодинамических функций. Различают:

· функции состояния, которые зависят только от состояния системы и не зависят от пути, по которому это состояние получено;

· функции перехода (процесса), значение которых зависит от пути, по которому происходит изменение системы.

Примеры функций состояния: внутренняя энергия U, энтальпия H, энергия Гельмгольца F, энергия Гиббса G, энтропия S. Термодинамические переменные – объем V, давление p, температуру T – также можно считать функциями состояния, т.к. они однозначно характеризуют состояние системы. Примеры функций перехода: теплота Q и работа A.

Термодинамические функции обычно относят к одному моль вещества.

Рассмотрим следующие характеристические функции: внутреннюю энергию (U), энтальпию (H), энтропию (S) и энергию Гиббса (G).

Термодинамический процесс - это любой процесс, при котором изменяется хотя бы одна характеристическая функция.

Процессы могут быть самопроизвольными и вынужденными.

Самопроизвольныйпроисходит без воздействия окружающей среды. Любой самопроизвольный процесс стремится привести систему в состояние равновесия – состояние, из которого система не может выйти без внешнего воздействия.

Вынужденный - происходит под влиянием внешних воздействий.

Процессы делятся на обратимые и необратимые.

Обратимые процессы - процессы, после протекания которых в системе не обнаруживается никаких изменений. Большинство физико-химических процессов обратимо, т.е. в зависимости от условий они могут протекать как в прямом, так и в обратном направлении.

Необратимые - в ходе которых либо в системе, либо в среде происходят какие-либо изменения.

Закон Гесса позволяет определить, сколько выделяется или поглощается теплоты при протекании реакции. Закон Гесса:

Тепловой эффект химической реакции зависит только от начального и конечного состояния реагирующих веществ, но не зависит от промежуточных стадий реакции, т.е. от пути протекания реакции.

Также существует следствия из закона Гесса (оно применяется чаще, чем сам закон и позволяет рассчитать тепловой эффект реакции):

1. Тепловой эффект реакции равен разности между суммой теплот образования конечных продуктов и суммой теплот образования исходных веществ.

∆H _{х. р.} = ∑∆Н_{f продуктов} - ∑∆Н_{f исх. веществ}

∆H _{х. р.} – тепловой эффект химической реакции,

∑∆Н_{f продуктов} – сумма теплот образования продуктов реакций с учётом стехиометрических коэффициентов,

∑∆Н_{f исх. веществ} – сумма теплот образования исходных веществ реакций с учётом стехиометрических коэффициентов.

2. Тепловой эффект реакции равен разности между суммой теплот сгорания исходных веществ и суммой теплот сгорания продуктов реакции.

∆H _{х. р.} = ∑∆Н_{сгор исх. веществ} - ∑∆Н_{сгор продуктов}

∆H_{х. р.} – тепловой эффект химической реакции,

∑∆Н_{сгор исх. веществ} – сумма теплот сгорания исходных веществ реакций с учётом стехиометрических коэффициентов,

∑∆Н_{сгор продуктов} – сумма теплот сгорания продуктов реакций с учётом стехиометрических коэффициентов.

Энтропия – количественная мера беспорядка системы.

Наименьшую энтропию имеют идеально правильно построенные кристаллы при абсолютном нуле. С увеличением температуры энтропия всегда возрастает.

Изменение энтропии реакции равно разности между суммой энтропии конечных продуктов и суммой энтропии исходных веществ.

∆S_{х. р.} = ∑S_{продуктов} - ∑S_{исх. веществ}

Суммирование происходит с учетом стехиометрических коэффициентов, стоящих перед веществами в уравнении химической реакции.

Для того чтобы учесть как тепловой (энтальпия), так и вероятностный (энтропия) факторы, действующие на систему, применяется энергия Гиббса.

∆G = ∆Н - T∆S

Характер изменения энергии Гиббса позволяет судить о принципиальной возможности самопроизвольного протекания процессов.

Самопроизвольно могут проходить процессы только из менее устойчивого состояния в более устойчивое, т.е. с уменьшением энергии.

∆G < 0 - реакция может протекать самопроизвольно (термодинамически возможна).

∆G > 0 - реакция не может протекать самопроизвольно (термодинамически невозможна).

∆G = 0 - система находится в состоянии равновесия.

Необходимо учитывать, что отрицательное значение ∆G той или иной реакции указывает только на возможность ее протекания. В действительности реакция может при этом и не наблюдаться. Дело в том, что скорость ее может быть малой. Тогда, несмотря на соблюдение условия ∆G < 0, реакция практически не будет протекать. В этих случаях для увеличения скорости реакции необходимо подобрать катализатор. Такое положение особенно часто наблюдается при низких температурах.

Температура, при которой в системе наступает равновесие, называется равновесной температурой (Т_р). Если система находится в равновесии, тогда ∆G = 0

Т_р = ∆Н/∆S

Изменение энергии Гиббса химической реакции равно разности между суммой энергий Гиббса образования конечных продуктов и суммой энергий Гиббса образования исходных веществ.

∆G_{х. р.} = ∑∆G_{продуктов} - ∑∆G_{исх. веществ}

Суммирование происходит с учетом стехиометрических коэффициентов, стоящих перед веществами в уравнении химической реакции.

В расчётах чаще используют термодинамические функции состояния системы (H, S, G) в стандартном состоянии. Стандартным состоянием вещества при данной температуре, называется его состояние в виде чистого вещества при давлении (в случае газов – при парциальном давлении данного газа), равном нормальному атомсферному давлению (101325 кПа или 760 мм рт ст). Условия, при которых все участвующие в реакции вещества находятся в стандартных состояниях, называется стандартными условиями протекания реакции. Отнесённые к стандартным условиям изменения соответствующих величин называются стандартными изменениями и их обозначение снабжается верхним индексом: DH⁰ – стандартное изменение энтальпии химической реакции (или стандартная энтальпия реакции); DS⁰ – стандартное изменение энтропии химической реакции; DG⁰ – стандартное изменение энергии Гиббса химической реакции.

Пример 46.Теплота растворения безводного хлорида стронция равна -48 кДж, а теплота растворения кристаллогидрата SrCl₂•6H₂0 равна +31 кДж. Вычислить теплоту гидратации хлорида стронция.

Дано:

ΔН₁(SrCl₂) = -48 кДж; ΔН₂(SrCl₂) = +31 кДж .

Найти: теплоту гидратации хлорида стронция.

Решение:

Безводный хлорид стронция - это SrCl₂, при растворении получаем раствор SrCl_2(р-р). Также, если оставить хлорид стронция на воздухе, то он будет присоединять воду из воздуха и превращаться в кристаллогидрат, который при растворении также дает раствор хлорида стронция.

ΔН₁

1.SrCl₂ SrCl_2(р-р)

ΔН₂

2.SrCl₂• 6H₂O SrCl_2(р-р)

ΔН₃

3.SrCl₂ SrCl₂• 6H₂O

∆Н₁ - теплота растворения безводного хлорида стронция;

∆Н₂ - теплота растворения кристаллогидрата,

∆Н₃ - теплота гидратации хлорида стронция (т.е. теплота перехода хлорида стронция в кристаллогидрат),

∆Н₁= ∆Н₃ + ∆Н₂;

∆Н₃ = ΔН₁(SrCl₂) - ΔН₂(SrCl₂) = -48 - 31 = -79 (кДж/моль)

Ответ: Теплота гидратации хлорида стронция составляет -79 кДж/моль.

Пример 47.Рассчитайте теплоту сгорания метана и количество теплоты, которое выделится при сгорании 100 дм³ этого вещества.

Дано:

V(CН₄)= 100 дм³.

Найти:

ΔΗ_сгор⁰ (CН₄), Q - ?

Решение:Под теплотой сгорания вещества подразумевают тепловой эффект реакции окисления молекулярным кислородом одного моль этого соединения с образованием высших оксидов. В случае органического соединения продуктами окисления обычно бывают СО_2(г) и Н₂О_(ж).

Реакцию сгорания метана можно представить уравнением:

СН_4(г) + 2О_2(г) ® СО_2(г) + 2Н₂О_(ж)

Используя следствие закона Гесса и стандартные энтальпии образования веществ (Приложение 4 табл. 1), определяем изменение энтальпии при протекании реакций:

ΔΗ⁰_сгор= ΔΗ⁰(СO_{2 (г)}) +2ΔΗ⁰(Н₂О_(ж)) - ΔΗ⁰(СН_{4 (г)}).

или ΔΗ⁰ = -393,5 + 2(-241,8) ( ((74,9) = (890,31 (кДж/моль).

ΔΗ⁰ = –Q, следовательно, при сгорании одного моль СН₄ выделяется 890,31 кДж/моль теплоты.

Рассчитаем количество моль метана:

n(СН₄) = 100 /22,4 = 4,46 (моль)

Количество теплоты при сгорании 4,46 моль метана составит:

4,46 ∙ 890,31= 3970,8 (кДж)

Ответ: При сгорании 100 дм³ выделится 3970,8 кДж тепла.

Пример 48.Вычислите ΔH⁰_х.р., ΔS⁰_х.р., ΔG⁰_х.р. реакции, протекающей по уравнению:

Fe₂O_3(кр) + 3С_{(графит)} = 2Fe_(кр) + 3CO_(г)

Возможна ли реакция восстановления Fe₂O₃ углеродом при температурах 500 и 1000 К?

Дано:

Fe₂O_3(кр) + 3С_{(графит)} = 2Fe_(кр) + 3CO_(г)

Т₁ =500 К

Т₂ = 100 К

Найти: ΔH⁰_х.р., ΔS⁰_х.р., ΔG⁰ _х.р.-?

Решение

∆H_х.р. = ∑∆Н_{f продуктов} - ∑∆Н_{f исх. веществ}

ΔH⁰_х.р = (3•∆Н⁰₂₉₈CO_(г)) + 2•∆Н⁰₂₉₈Fe_(кр)) - (∆Н⁰₂₉₈ Fe₂O_3(кр) +3∆Н⁰₂₉₈ С_(тв))= =(3(-110,53) + 2•0) - (-822,16+3•0) = -331,56 + 822,10 = +490,57 (кДж);

ΔS⁰_х.р = (3•S⁰₂₉₈CO_(г)) + 2•S⁰₂₉₈Fe_(кр)) - (S⁰₂₉₈ Fe₂O_3(кр) +3S⁰₂₉₈ С_(тв)) (2•27,15 + 3•197,55) - (87,45 + 3•5,74) = 542,28 (Дж/К)

Энергию Гиббса при соответствующих температурах находим из соотношения ΔG₅₀₀ = ΔH⁰_х.р. - ΔS⁰_х.р. •T₁/1000= 490,57 - 500•542,28/1000 = 219,43 кДж;

ΔG₁₀₀₀ = ΔH⁰_х.р. - ΔS⁰_х.р. •T₂/1000=490,57 - 1000•542,28/1000 = -51,71 (кДж)

Так как ΔG₅₀₀ > 0, а ΔG₁₀₀₀ < 0, то восстановление Fe₂O₃ углеродом возможно при 1000 К и невозможно при 500 К.

Ответ: ΔH⁰_х.р. составит +490,57 кДж, ΔS⁰_х.р. составит 542,28 Дж/К, а так как ΔG₅₀₀ > 0, а ΔG₁₀₀₀ < 0, то восстановление Fe₂O₃ углеродом возможно при 1000 К и невозможно при 500 К.

Комплексная задача № 9

В полом технологическом аппарате ёмкостью V₁ л (столбец 3), рассчитанном на максимальное давление p₁ атм. (столбец 4) проводят исследования по определению пожаровзрывоопасных показателей взрывчатого вещества.

Задания:

1.Определить максимальную массу вещества, которую можно подавать в технологический аппарат, если разложение этого вещества при взрыве протекает по реакции, указанной в варианте задания (температура взрыва t^oC – столбец 5)?

2.Определить объем газа (приведенный к н.у.), который получается при взрыве 1 кг взрывчатого вещества.

3.Определить теплоту взрывчатого разложения вещества (∆H _{х. р.}), оцентите не прибегая к расчётам ΔS⁰_х.р..

4.Какие процессы окисления и восстановления соответствуют уравнению реакции.

Таблица 22

Варианты заданий

№ варианта	Уравнение реакции, протекающей при взрыве	V1, л	p1, атм	toC
1.	тротил 2C6H2CH3(NO2)3 = 3N2 + 12CO + 5H2 + 2C	0,50

Окончание таблицы 22

2.	нитрометан 4CH3NO2 = 4CO + 4H2Oг + 2H2 + 2N2	0,25
3.	нитроглицерин (в динамите с 25% кремнезёма) 2C3H5O3(NO2)3 = 6CO2 + 5H2Oг + 3N2 + 0,5O2	1,00
4.	тетранитропентаэритрит (тэн) C(CH2ONO2)4 = 3,1CO2 + 1,9CO + 3,9H2Oг + 0,1H2 + 2N2	0,15
5.	пикриновая кислота 2C6H2(NO2)3OH = 3N2 + CO2 + 11CO + H2Oг + 2H2	0,10
6.	аммонит (21% тротила, 79% аммиачной селитры) 2C6H2CH3(NO2)3 + 27,7NH4NO3 = 14CO2 + 60,4H2Oг + 30,7N2 + 3,35O2	2,00
7.	гексоген C3H6N6O6 = 3H2O + 3CO + 3N2	0,20
8.	тротил 2C6H2CH3(NO2)3 = 3N2 + 12CO + 5H2 + 2C	0,7
9.	нитрометан 4CH3NO2 = 4CO + 4H2Oг + 2H2 + 2N2	0,85
10.	нитроглицерин (в динамите с 25% кремнезёма) 2C3H5O3(NO2)3 = 6CO2 + 5H2Oг + 3N2 + 0,5O2	0,40
11.	тетранитропентаэритрит (тэн) C(CH2ONO2)4 = 3,1CO2 + 1,9CO + 3,9H2Oг + 0,1H2 + 2N2	0,75
12.	пикриновая кислота 2C6H2(NO2)3OH = 3N2 + CO2 + 11CO + H2Oг + 2H2	0,25
13.	аммонит (21% тротила, 79% аммиачной селитры) 2C6H2CH3(NO2)3 + 27,7NH4NO3 = 14CO2 + 60,4H2Oг + 30,7N2 + 3,35O2	1,00
14.	гексоген C3H6N6O6 = 3H2O + 3CO + 3N2	0,15
15.	тротил 2C6H2CH3(NO2)3 = 3N2 + 12CO + 5H2 + 2C	0,90
16.	нитрометан 4CH3NO2 = 4CO + 4H2Oг + 2H2 + 2N2	0,10
17.	нитроглицерин (в динамите с 25% кремнезёма) 2C3H5O3(NO2)3 = 6CO2 + 5H2Oг + 3N2 + 0,5O2	0,80
18.	тетранитропентаэритрит (тэн) C(CH2ONO2)4 = 3,1CO2 + 1,9CO + 3,9H2Oг + 0,1H2 + 2N2	0,27
19.	пикриновая кислота 2C6H2(NO2)3OH = 3N2 + CO2 + 11CO + H2Oг + 2H2	0,50
20.	аммонит (21% тротила, 79% аммиачной селитры) 2C6H2CH3(NO2)3 + 27,7NH4NO3 = 14CO2 + 60,4H2Oг + 30,7N2 + 3,35O2	1,50
21.	гексоген C3H6N6O6 = 3H2O + 3CO + 3N2	2,00
22.	тротил 2C6H2CH3(NO2)3 = 3N2 + 12CO + 5H2 + 2C	0,70
23.	нитрометан 4CH3NO2 = 4CO + 4H2Oг + 2H2 + 2N2	0,55
24.	нитроглицерин (в динамите с 25% кремнезёма) 2C3H5O3(NO2)3 = 6CO2 + 5H2Oг + 3N2 + 0,5O2	1,20

Основные понятия химической кинетики

Химические реакции протекают с различной скоростью. Некоторые реакции протекают за несколько секунд, некоторые за несколько лет. Химические реакции бывают:

1.Гомогенными – реакции, протекающие в гомогенной среде (реагирующие вещества находятся в одном агрегатном состоянии).

2.Гетерогенными– реакции, протекающие в гетерогенной среде (реагирующие вещества находятся в разных агрегатных состояниях).

Скоростью реакции в гомогенной среде называется изменение концентрации какого-либо из веществ, вступающих в реакцию или образующихся в результате её, происходящее за единицу времени.

,

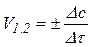где Δс – изменение концентрации веществ, участвующих в реакции, Δτ – изменение времени протекания реакции, v_1,2 – скорость прямой и обратной реакции.

Скорость химической реакции зависит от следующих факторов:

1.Природы реагирующих веществ.

2.Концентрации реагирующих веществ.

3.Температуры.

4.Наличия катализатора.

Влияние природы и концентрации реагирующих веществ определяется законом действующих масс.

Закон действующих масс – при постоянной температуре скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ в степенях их стехиометрических коэффициентов.

Например, для реакции:

2СО(г) + О₂(г) = 2СО₂(г)

v_х.р. = k ×[CO]² × [O₂],

где k – константа скорости реакции зависит от природы реагирующих веществ и температуры.

Концентрации твердых веществ остаются постоянным и в законе действующих масс не записываются. Например, для реакции:

С_(тв) + О_2(г) = СО_2(г)

v_х.р. = k × [O₂]

Изменение концентрации газообразных веществ пропорционально изменению давления.

Исходя из вышесказанного, скорость химической реакции при постоянной температуре прямо пропорциональна произведению концентрации реагирующих веществ в степенях их стехиометрических коэффициентов:

-dC/dτ = К_V•Сⁿ_A• Сⁿ_B = К_V•[A]ⁿ•[B]^m,

-dC/dτ – истинная скорость химической реакции по реагентам, К_V- константа скорости химической реакции, С_A, С_B – концентрация вещества А и В, n, m - стехиометрические коэффициенты.

Уравнение, связывающее скорость химической реакции с концентрацией реагирующих веществ, называется кинетическим уравнением.

Константа скорости химической реакции характеризует скорость реакции при концентрации раегирующих веществ, равных 1 (моль/л).

Пример 49. Определить, как изменится скорость реакции 2SO₂(г) + O₂(г) = SO₃(г) при увеличении давления в 2 раза.

Дано: 2SO₂ + O₂ = SO₃; 2•Р₁ = Р₂.

Решение:

1.Запишем для данной реакции выражение закона действующих масс.

v = k × [SO₂]² × [O₂]

Тогда для первого и второго момента времени скорости химической реакции будут следующими:

v₁ = k × [SO₂]²₁ × [O₂]₁

v₂ = k × [SO₂]²₂ × [O₂]₂

2.При увеличении давления в 2 раза концентрации газообразных веществ также увеличатся в 2 раза.

[SO₂]₂ = 2 [SO₂]₁

[O₂]₂ = 2 [O₂]₁

3.Заменим концентрации после увеличения давления на начальные в уравнении для v₂

v₂ = k × (2[SO₂]₁)² × (2[O₂]₁) = k × 4[SO₂]₁² × 2[O₂]₁ = 8 × k × [SO₂]₁² × [O₂]₁

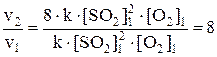
Ответ: Скорость химической реакции увеличится в 8 раз.

Влияние температуры на скорость химической реакции определяется законом Вант-Гоффа:

При повышении температуры на каждые 10 ⁰С скорость гомогенной химической реакции увеличивается в 2-4 раза.

Закон Вант-Гоффа выражается соотношением:

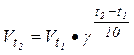
где v_t1 - скорость реакции при температуре t₁, v_t2 - скорость реакции при температуре t₂, g - коэффициент Вант-Гоффа, показывающий во сколько раз увеличится скорость реакции при увеличении температуры на 10 градусов.