Основы теории движения ГЖС в скважине
[Сахаров В.А. и др. Эксплуатация нефтяных скважин. РГУ, 2008г.]
[Стр6]
При эксплуатации нефтяных скважин имеется большое многообразие структурных форм ГЖС – потоков. В зависимости от давления насыщения и обводненности продукции в скважине возможно существование однофазного, двухфазного или трехфазного течения.
Фаза – однородная по химическому составу и физическим свойствам часть системы, отделяемая от другой части этой системы поверхностью раздела. Например: нефть-вода, газ-жидкость – это двухфазные системы, раствор соли в воде – однофазная система.
ГЖС – это двухфазная или трехфазная система многокомпонентной эмульсии. Компонент – это химически индивидуальные вещества: вода, метан и т.п. Для нефтяных месторождений возможно существование следующих форм продукции:
- водонефтяная: промысловая вода + нефть
-нефтегазовая: промысловая нефть + промысловый газ
-водонефтегазовая: пластовая вода + промысловая нефть + промысловый газ.
Промысловая нефть – частично раздробленная пластовая нефть, находящаяся в эксплуатационной колонне, насосном оборудовании, НПТ и трубопроводной системы сбора.
Промысловый газ – смесь пластового газа, паров нефти и паров пластовой воды. В случае если, давление в скважине ниже давления насыщения пластовой нефти газом, то из нефти начинает выделяться газ. При этом непрерывно изменяется содержание газовой фазы в ГЖС, что ведет к изменению расходной характеристики потока.
При изменении давления и температуры происходит изменение физико-химических, характеристик отдельных фаз и границ их раздела: плотности, вязкости, поверхностного натяжения и т.д.
Это диктует необходимость учета многообразия структуры форм, а так же изменяющихся расходных характеристик и физико-химических свойств скважинной продукции.
Знания о течении двухфазной, а тем более трехфазной систем основывается больше на эмпирических исследованиях. [Рис1]
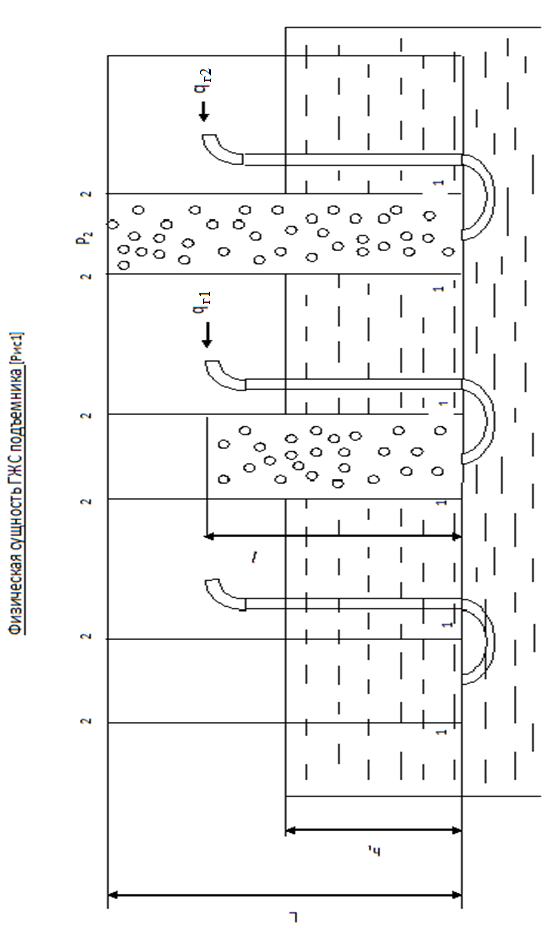
А - вертикальная трубка опущена на глубину h1 , жидкость плотностью ρж . Через трубку Б к башмаку подъемника может подаваться рабочий агент.
Давление на башмаке в сечении 1 - 1: Р1 = ρж ∙ g ∙ h1 – гидростатическое давление.
При подаче газа через трубку Б с расходом qг1 он будет всплывать в жидкости. Уходя в атмосферу. В трубке А образуется ГЖС с плотностью ρс меньшей плотности воды (жидкости).
На уровне 1-1 давление одинаково и в емкости и в трубке А, то для создания его смесь меньшей плотности требуется большей высоты L:
ρc ∙ g ∙ L = ρж ∙ g ∙ h1
При увеличении расхода газа газосодержание в трубке А растет, значит плотность смеси уменьшается, при этом увеличивается высота столба смеси L. При каком-то газосодержании (расход qг0) уровень жидкости в подъемнике достигает устья – сечения 2-2, а при расходе газа больше q г0 подъемник начнет работать.
Работает подъемник при qг2 с дебитом qж. Давление в подъемнике затрачивается на преодоление веса столба ГЖС и потери на трение:
Р1 – Р2 = ρс ∙ q ∙ L + Ртс
Р1 – давление на башмак;
Р2 – давление в сечении 2 – 2 (на устье).
Причины подъема жидкости при вводе газа в вертикальную трубку.
Д. Верслюис – подъем жидкости в газожидкостном подъемнике в основном за счет энергии распределяющегося газа. Но в принципе, подъем жидкости ρж может быть осуществлен и в случае применения не расширяющегося агента – например нерастворимой жидкости или твердых тел – полиэтиленовых шариков меньшей плотности, т.к. в трубке А будет смесь жидкости и твердых тел шариков меньшей плотности.
Белогорцев Г.И. и др. – основная причина подъема жидкости в газожидкостном подъемнике (ГЖП) является относительная скорость газа – т.к. газ всплывая в жидкости увлекает за собой за счет сил трения близ лежащие слои жидкости. Но подъем в трубке А можно осуществить взаиморастворяющуюся жидкость (спирт) меньшей плотности – тоже будет работать ГЖП.
Багдасаров В.Г. и др. считают, что основные причины подъема жидкости в ГЖП является работа газового пузыря или комплекса пузырьков как негерметичного поршня с потерей по пути части поднимаемой жидкости. На всплывающий пузырек действует Архимедова сила силы сопротивления движения пузырька в жидкости. Имеем совокупность внутренних сил движущейся ГЖС и поэтому совершать работу по подъему смеси эти силы не могут.
О не герметичном поршне в применении к подъему ГЖС можно говорить лишь при пробковой структуре течения смеси. Когда пузырьки газа перекрывают практически все сечение трубы и имеют реакцию со сторонами ее стенок, но это ведет к низкой эффективности подъемника, т.к. идет деформация газового пузыря.
Резюме
Основной причиной подъема жидкости в составе ГЖС является снижение плотности ее (ГЖС) за счет подачи к башмаку подъемника рабочего агента с плотностью, меньшей, чем плотность поднимаемой жидкости. При этом непринципиально ни агрегатное состояние рабочего агента, ни другие его физико-химические свойства ( а свойства ПАВ – пенообразователей!!!)
Поэтому для подъема жидкости используют газ – наиболее эффективный рабочий агент. При применении газа плотность смеси в подъемнике снижается не только за счет объема рабочего агента, вводимого в башмаке подъемника, но и за счет расширения газа (пузырьков) по мере подъема смеси к устью.
Структурные формы газожидкостного потока
При подъеме нефти от забоя до устья возможны различные структуры потока. Когда давление в необводнившейся скважине больше давления насыщения в скважине движется однофазный поток. При снижении давления в скважине ниже давления насыщения нефти газом, из нее начинает выделяться газ, образуя двухфазный поток ГЖС. В нефтяных скважинах возможно существование следующих структур потока [Рис2]:
Структуры потока [Рис2]
| пузырьки газа |
| круппные газовые включения |
| h |
| f |
| газ |
| жидкость виде капелек |
| жидкость оттесне – нная к стенке (пленка нефти) |
| газовая фаза |
| капли жидкости |
1. Пузырьковая – с равномерно распределенными в нем пузырьками газа диаметром до 1 мм. Пузырьковая (1) структура преобладает при фонтанном и насосном способах эксплуатации т.к. в нефти есть много ПАВ – поэтому пузырьки прочные, эластичные, коалесценция не происходит.
2. Пробковая – снарядная, чёточная, чередование элементов газовой фазы (как снаряда) и жидкостных перемычек. Пробковая структура в нефтяных скважинах наблюдается редко но часто прослеживается при лабораторных исследованиях ГЖС.
3. Переходная – вспененная - достигается при движении потока ГЖС несколько м/с. Пробки газа увлекают за собой жидкость со скоростью превышающей течение однофазной жидкости, что приводит к стеканию жидкости по стенке трубы, создавая дополнительную силу трения, направленную против течения потока ГЖС. Течение неустойчиво, появляются пульсации. Крупные газовые включения постоянно дробятся и соединяются, жидкость насыщена мелкими пузырьками. Наблюдается при газонефтяном способе эксплуатации.
4. Кольцевая (стержневая) структура возникает при дальнейшем увеличении газосодержании потока. Жидкость оттесняется к стенке трубы, создавая пленки жидкости (нефти) с включениями газовых пузырьков или без них, - газовая фаза с каплями жидкости концентрируется в центре потока. Такая структура только в газонефтяных скважинах при больших удельных расходах газа – экономически нецелесообразна. При эксплуатации газовых скважин эта структура возможна при большой обводненности продукции.
5. Структура тумана – дисперсная структура – подавая жидкость переносится в виде мельчайших капелек в потоке газа. При этой структуре относительная скорость фаз ≈→0. Это характерно для газовых обводненных или газоконденсатных скважин.
При пробковой, переходной, кольцевой структурах образуются турбулентные ГЖС потоки, которые характеризуются неоднородностью движения ГЖС, пульсациями, колебательными процессами. Область существования структурной формы в вертикальном ГЖП зависит от соотношения гравитационных, инерционных сил, физико-химических свойств, фаз их расходов и т.д.
По данным Крылова А.П. и Лутошкина Г.С. границы перехода пузырьковой структуры в пробковую при движении воздухожидкостных смесей при данных P и T определяется по формуле:
qг.кр. = 1.75dт2.5 + 1.25qж
при qг < qг.кр. -структура пузырьковая
qг > qг.кр. –структура пробковая
qг – расход газа
qж- расход жидкости 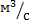
dт – внутренний диаметр трубы, м
Зависимость величины расходного газосодержания от критерия Фруда [Рис3]
| 0,8 |
| 0,6 |
| 0,4 |
| 0,2 |
| пробковая и вспененная |
| туманообразная и кольцевая |
| пузырьковая |
| β |
| Frc |
Дополнения
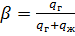 - расходное газосодержание.
- расходное газосодержание.
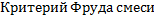 :
:
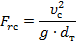
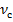 - скорость движения смеси;
- скорость движения смеси;
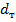 - диаметр трубы.
- диаметр трубы.
Механизм движения ГЖС в вертикальных трубах
Многие исследователи занимались влиянием на скорость всплытия пузырьков:
- размеров пузырьков;
- физических свойств флюидов и границ их раздела.
График зависимости скорости всплытия пузырьков в зависимости от их размеров или числа Рейнольдса.
Зависимость скорость всплытия пузырьков от диаметра пузырьков [Рис4]
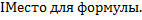 |
 |
 |
 |
 п п |
| dп |
При малых пузырьках сферической формы формула Стокса: (формула для определения скорости подъема):
 ∞ =
∞ = 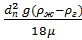
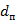 - диаметр пузырька;
- диаметр пузырька;
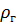 – плотность газа при данных термодинамических условиях;
– плотность газа при данных термодинамических условиях;
 – коэффициент динамической вязкости.
– коэффициент динамической вязкости.
Первая область ( 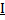 ) определяется предельными значениями Re
) определяется предельными значениями Re
Re = 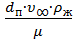 ≤ 2
≤ 2
Вторая область( 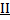 ) - форма сфероида. С увеличением числа Re закон движения пузырька в жидкости меняется.
) - форма сфероида. С увеличением числа Re закон движения пузырька в жидкости меняется.
Левич В.П. для Re от 50 до 1000 получил:
 ∞ =
∞ = 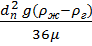 (x) – (ламинарное течение) Re
(x) – (ламинарное течение) Re 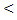 2300
2300
Но! Следы ПАВ в жидкости приводят к значительным отклонениям от зависимости (x). Более точная формула имеет более эмпирическое происхождение (Пиблс и Гарбер):
 ∞ = 0.13 g0.76
∞ = 0.13 g0.76 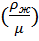 0.52 dп1.28
0.52 dп1.28
для условий: z< Re≤4(We3Ar2)0.214
где: We= 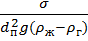 число Вебера
число Вебера
Ar = 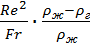 =
= 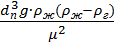 - число Архимеда.
- число Архимеда.
Fr = 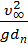 – число Фруда.
– число Фруда.
𝜎 - поверхностное натяжения награнице газ – жидкость. Т.е. формула Вебера учитывает 𝜎 для ПАВ.
Сфероиды двигаются по винтовой траектории.
В третьей области (  ) пузырьки еще больше сплющиваются, приобретают грибообразную форму и колеблются при движении.
) пузырьки еще больше сплющиваются, приобретают грибообразную форму и колеблются при движении.
В четвертой области ( 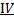 ) пузырьки неустойчивы и могут разрушаться на отдельные малые пузырьки. Диаметр пузырьков во второй и последующих областях – условный и определяется по формуле: dп =
) пузырьки неустойчивы и могут разрушаться на отдельные малые пузырьки. Диаметр пузырьков во второй и последующих областях – условный и определяется по формуле: dп = 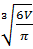
Для области (  ):
):
4(We3Ar2)0.214 < Re≤3,1(We3Ar2)0.25
Для этих условий скорость всплытия (Пиблс и Гарбер)
 ∞ = 1,91
∞ = 1,91 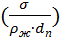 0.5 (xx)
0.5 (xx)
При больших числах Re наблюдается область движения, в которой скорость всплытия пузырька не зависит от его размера:
 ∞ = 1,181
∞ = 1,181 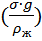 0.25 (xxx)
0.25 (xxx)
Формулы (хх) и (ххх) эмпирические.
Теоретическая формула Д.А. Франка-Каменецкого (исходя из условий равенства работ сил гидравлического сопротивления затраченной на уменьшение толщины пузырька, и изменения энергии раздела фаз):
 ∞ =
∞ = 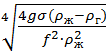
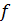 - коэффициент сопротивления движения пузыря.
- коэффициент сопротивления движения пузыря.
Скорость всплытия пузырьков в стесненных условиях
Скорость всплытия пузырька в трубе обычно гораздо больше, чем в неограниченном объеме жидкости, т.к . стенки трубы ограничивают возможность растекания, сплющивания пузырька, его дробление. Пузырек, стесненный стенками трубы, может иметь объем намного больший, объема в свободной жидкости, и кроме того приобретает обтекаемую форму. Поэтому скорость всплытия пузырьков в трубе кратно превышает максимальную скорость их всплытия в неограниченном объеме жидкости.
Мищенко И.Т. , Гуревич А.С. – экспериментально доказали, что в группе (в стесненных условиях) скорость всплытия маленьких пузырьков превышает скорость всплытия одиночного пузырька таких же размеров в 1.3 – 3 раза и зависит от безразмерного комплекса:
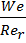 , где
, где 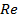 =
= 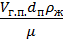 - критерий (число) Рейнольдса
- критерий (число) Рейнольдса
Vг.п.= 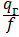 - приведенная скорость газа;
- приведенная скорость газа;
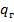 – расход газа при данных термодинамических условиях;
– расход газа при данных термодинамических условиях;
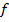 – площадь сечения труб.
– площадь сечения труб.
Получена формула:
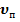 = 2,85
= 2,85  ∞[
∞[ 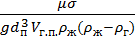 ]-0.25
]-0.25
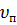 – скорость всплытия пузырьков в стесненных условиях.
– скорость всплытия пузырьков в стесненных условиях.
Безразмерные параметры потока ГЖС
Для описания процессов движения ГЖС часто применяются безразмерные параметры, так уравнение ГЖС можно записать в безразмерном виде путем деления на один из его членов или введением величины.
Безразмерными параметрами также называют критериями подобия, т.к. у подобных процессов одноименные критерии численно равны.
В общем виде критериальное уравнение установившегося изометрического течения ГЖС по трубам можно представить в виде:
Euc=f(  , Rec , We ,
, Rec , We , 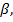
 ,
, 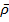 )
)
· Euc =  - критерий Эйлера является мерой взаимодействий гидравлических сопротивлений и динамического напора на рассматриваемом участке потока.
- критерий Эйлера является мерой взаимодействий гидравлических сопротивлений и динамического напора на рассматриваемом участке потока.
· 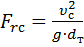 - число Фруда является критерием гравитационного подобия, определяющее отношение сил инерции к силе тяжести.
- число Фруда является критерием гравитационного подобия, определяющее отношение сил инерции к силе тяжести.
· 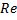 =
= 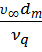 - число Рейнольдса характеризует гидродинамический режим потока смеси или фазы и являющейся мерой отношений сил инерции и молекулярного трения.
- число Рейнольдса характеризует гидродинамический режим потока смеси или фазы и являющейся мерой отношений сил инерции и молекулярного трения.
· We =  - критерий Вебера, характеризующий соотношение сил поверхностей натяжения и тяжести.
- критерий Вебера, характеризующий соотношение сил поверхностей натяжения и тяжести.
| Безразмерные симплексы |
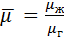
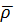 =
= 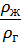
· Ar = 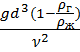 – критерий Архимеда, характеризующий соотношение подъемной силы и силы сопротивления вызываемой молекулярной массой.
– критерий Архимеда, характеризующий соотношение подъемной силы и силы сопротивления вызываемой молекулярной массой.
· Ku = 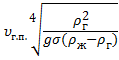 - критерий Кутателадзе, характеризующий условия начала деформации поверхности раздела фаз или начало структурных изменений в ГЖС-потоке под воздействием динамического напора архимедовой силы и поверхностного натяжения.
- критерий Кутателадзе, характеризующий условия начала деформации поверхности раздела фаз или начало структурных изменений в ГЖС-потоке под воздействием динамического напора архимедовой силы и поверхностного натяжения.
| Безразмерные приведенные скорости и относительная |
 ф.п. =
ф.п. = 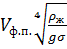
 о =
о = 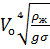
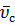 . =
. = 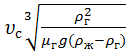 - безразмерная скорость смеси.
- безразмерная скорость смеси.
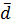 т =
т =  ≈
≈ 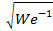 - безразмерный диаметр трубы
- безразмерный диаметр трубы
· 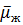 =
= 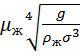 =
= 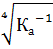 –безразмерная динамическая вязкость жидкости.
–безразмерная динамическая вязкость жидкости.
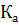 =
= 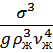 =
= 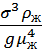
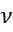 =
= 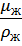 - кинематическая вязкость
- кинематическая вязкость
· 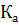 - критерий Капицы характеризующий волновые процессы при движении пленок жидкости и вертикальной поверхности.
- критерий Капицы характеризующий волновые процессы при движении пленок жидкости и вертикальной поверхности.
· 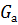 =
=  - критерий Галилея, характеризующий соотношение сил молекулярного трения и сил тяжести.
- критерий Галилея, характеризующий соотношение сил молекулярного трения и сил тяжести.
Кинематические параметры потока ГЖС
1. Скорость течения ГЖС
Vc = 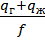
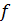 – площадь сечения трубы;
– площадь сечения трубы;
 - расход газа;
- расход газа;
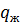 - расход жидкости.
- расход жидкости.
2. Расходное газосодержание
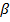 =
= 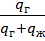 =
= 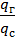 - расход газа к расходу смеси
- расход газа к расходу смеси
3. Истинное газосодержание – это относительный объем газа в смеси при данных термодинамических условиях:
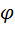 =
=  =
= 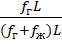
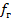 - площадь сечения трубы занятая газом;
- площадь сечения трубы занятая газом;
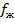 - площадь сечения трубы занятая жидкостью.
- площадь сечения трубы занятая жидкостью.
| Распределение площади сечения между фазами ГЖС |
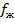 |
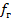 |
Газ Жидкость
тогда: 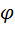 =
= 
4. Скорость движения газа
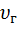 =
= 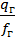
5. Скорость движения жидкости
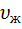 =
= 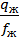
(4) и (5) – это скорость движения фаз, найденные через расходы фаз ( 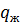 и
и  ) при термодинамических условиях, отнесенных к площади сечения занятой этой фазой.
) при термодинамических условиях, отнесенных к площади сечения занятой этой фазой.
6. Формулировка 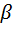 =
= 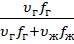
Видно, что если 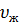 =
=  , то
, то 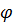 =
= 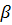 ( т.е.
( т.е. 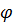 =
= 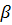 =
= 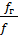 );
);
Если 
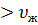 , ∞ имеет место относительная скорость - истинное газосодержание меньше расходного:
, ∞ имеет место относительная скорость - истинное газосодержание меньше расходного: 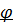 <
< 
н.з. в восходящем потоке ГЖС в нефтяных скважинах всегда существует относительная скорость газа, и чем больше относительная скорость, тем меньше 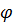 .
.
7. Относительная скорость – с этой скоростью пузырьки газа опережают жидкость:
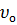 =
=  -
- 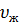
Размерные параметры. Плотность ГЖС.
ρс = 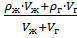
очевидно из уравнения баланса:
ρс(Vж + Vг) = ρж∙ Vж +ρг∙ Vг
объем масса масса
смеси жидкости газа
С учетом формулы в п.3. ρс = ρс (1- 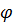 ) + ρс ∙
) + ρс ∙ 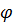
Получено через уравнение баланса масс: Vc ∙ ρс = Vc∙ ρж(1- 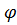 )+ Vc
)+ Vc  ∙ ρг ∙
∙ ρг ∙ 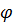
ρс = ρж(1- 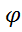 )+ρг ∙ )+ρг ∙ 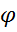 |
тогда плотность ГЖС:
