Средняя концентрация фотонов со всеми частотами

Фотонный газ

Фотон – квант электромагнитной волны ввел Альберт Эйнштейн в 1905 г. Название от др.-греч. jwtoV – «свет» дал Гильберт Льюис в 1926 г. Импульс и энергия фотона в вакууме определяются длиной и частотой волны

,

, (4.53)

где

; ;

C – скорость света. Спин фотона , он является бозоном. Масса фотона равна нулю, он движется со скоростью света. Теория относительности допускает только две проекции спина – по- и против скорости, что соответствует двум типам поляризации света. Тогда кратность вырождения по спину

.

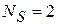Фотонный газ. Электромагнитное излучение в полости непрерывно испускается и поглощается заряженными частицами стенок, переходящими с одного энергетического уровня на другой. Для равновесной системы температура стенок одинаковая и постоянная. Все точки и направления полости равноправные. Излучение испускается и поглощается порциями – квантами, которые образуют в полости равновесный фотонный газ. Состояние фотонного газа является волной и характеризуется частотой.

Плотность состояний. В единичном объеме, в интервале частот находится число состояний, т. е. число независимых волн:

. (4.54)

Например, для излучения красного цвета l = 0,6 мкм, w @ 3×10¹⁵ рад/с, в объеме и в единичном интервале частоты находится число волн g(w) = 3,38×10⁴ м^–3.

Доказательство (4.54). Элемент фазового объема кванта в сферических координатах

.

В силу симметрии фотоны распределены равномерно по объему полости и по направлениям движения. Интегрируем по направлениям в пределах телесного угла и по единичному объему полости. Получаем фазовый объем, занятый фотоном с модулем импульса в интервале :

.

Заменяем

,

получаем

.

Для числа состояний

В единице объема полости находим

.

Химический потенциал. У фотона нет заряда. Число фотонов меняется при излучении и поглощении света заряженными частицами, поэтому химический потенциал фотона не может быть получен из условия нормировки на число частиц.

Условие термодинамического равновесия фотонного газа в виде минимума свободной энергии требует

.

Для теплового излучения в полости объемом V, испускаемого стенками с температурой Т, химический потенциал определяется в виде (2.61а)

,

тогда

m = 0. (4.55)

Химический потенциал теплового равновесного фотонного газа равен нулю.

Для нетепловых фотонов, возникающих при соединении электронов e и дырок h полупроводникового светодиода в реакции

,

вклад в свободную энергию дают фотон, электрон и дырка. Условие минимума получает вид

.

Учитывая

,

и разные знаки у химических потенциалов электронов и дырок, находим

, (4.55а)

где e_F –энергия Ферми соответствующей частицы. Выполняется

.

Аналогично определяется химический потенциал фотонов, создаваемых газовым разрядом, лазером, люминесцентным источником.

Число фотонов. Из распределения Бозе–Эйнштейна (4.10)

получаем среднее число тепловых фотонов в волне с частотой w

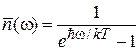. (4.56)

Учитывая число волн (4.54), находим среднюю концентрацию фотонов с частотой в интервале :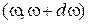

. (4.57)

Средняя концентрация фотонов со всеми частотами

.