При постоянной температуре скорость химической реакции прямо пропорциональна произведению концентраций реагирующих веществ в степенях их стехиометрических коэффициентов

aa + bb + . . . ® . . .

V = k • [A]^a • [B]^b • . . .

(используется молярная концентрация)

Константа скорости реакции k зависит от природы реагирующих веществ, температуры и катализатора, но не зависит от значения концентраций реагентов.

Физический смысл константы скорости заключается в том, что она равна скорости реакции при единичных концентрациях реагирующих веществ.

Для гетерогенных реакций концентрация твердой фазы в выражение скорости реакции не входит.

Например:

С_{(графит)} + О_2(г) → СО₂

V_{пр.реакц.} = k₁∙S_c ∙ C(O₂) = k ∙ C(O₂)

Твёрдые вещества реагируют только с поверхности, константа будет зависеть от площади сосуда (S_c), но во времени не меняется.

Порядком реакции называется сумма всех показателей степеней концентрации в кинетическом уравнении (m + n).

ma + nb ® . . .

V = k • [A]^m • [B]ⁿ

Различают реакции первого, второго и третьего порядка. Известны химические реакции нулевого порядка, когда m + n = 0. В случае нулевого порядка скорость реакции не зависит от концентрации реагентов. В качестве примера можно привести реакцию гидрирования этилена на платине:

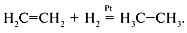
Cкорость данной реакции определяется поверхностью катализатора и не зависит от концентраций реагентов:

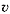= k ∙ [C₂H₄]⁰[H₂]⁰.

Встречаются химические реакции первого порядка (m + n = 1). К реакциям первого порядка относятся, как правило, процессы разложения. Известно небольшое число таких реакций. Например, разложение азометана в газовой фазе является реакцией первого порядка:

СН₃–N=N–СН₃ = С₂Н₆ + N₂.

Скорость этой реакции зависит только от концентрации азометана:

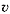= k ∙ [(СH₃)₂N₂].

Процессы разложения:

2N₂О₅ = 4NО₂ + O₂, N₂О₄ = 2NО₂

тоже относятся к реакциям первого порядка.

Не все реакции разложения имеют первый порядок. Так, реакциям разложения:

2NОСl = 2NO + Cl₂, 2О₃ = 3O₂

соответствует второй порядок.

Окисление бромоводорода кислородом: 4HBr + O₂ = 2Br₂ + 2H₂O

тоже относится к реакциям второго порядка, несмотря на то, что согласно уравнению с одной молекулой кислорода реагируют четыре молекулы бромоводорода. Это несоответствие записи уравнения реакции и выражения для ее скорости:

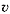= k ∙ [О₂][HBr]

связано с тем, что данная реакция протекает в три стадии:

1) НВr + О₂ = HО₂Вr (лимитирующая стадия),

2) НО₂Вr + НBr = 2НОВr,

3) 2НОBr + 2НВr = 2Н₂О + 2Вr₂,

_НВr + О₂ = 2Н₂О + 2Вr₂.

Первая стадия в представленном механизме медленная. Вторая и третья стадии – быстрые, не лимитирующие процесс. Вот почему взаимодействие бромоводорода с кислородом относится к реакциям второго порядка – по уравнению 1) такой порядок имеет лимитирующий процесс.

Реакция 2NО (г.) + О₂ (г.) = 2NО₂ (г.) –

реакция второго порядка по NO и первого порядка по О₂, в целом же – это реакция третьего порядка. Выражение для скорости реакции получения NО₂:

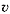= k ∙ [NO]²[О₂]

соответствует стехиометрии реакции, что является признаком ее одностадийности, одновременного столкновения трех молекул, приводящего к появлению диоксида азота.

Встречаются также реакции дробного порядка. К числу таких реакций относится образование фосгена в газовой фазе:

СО + Cl₂ = СОCl₂.

Выражение для скорости этой реакции имеет следующий вид:

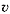= k ∙ [CO][Cl₂]^3/2.

Разложение озона в присутствии хлора: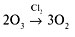

также является реакцией дробного порядка, протекающей со скоростью: 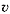= k ∙ [О₃]^3/2.

Лишь в редких случаях уравнение реакции отражает истинный механизм процесса, который обычно сложен и многостадиен.

Число молекул реагентов, участвующих в простой одностадийной реакции, состоящей из одного элементарного акта, называется молекулярностьюреакции.

Мономолекулярная реакция: C₂H₆ = 2 CH₃^.

Бимолекулярная реакция: CH₃^. + CH₃^. = C₂H₆

Примеры относительно редких тримолекулярных реакций:

2 NO + O₂ = 2 NO₂

2 NO + Cl₂ = 2 NOCl

H^. + H^. + Ar = H₂ + Ar

Большинство реакций являются многостадийными, даже если они описываются простыми стехиометрическими уравнениями. В этом случае скорость реакции зависит от лимитирующей стадии.

3. Температура. При повышении температуры на каждые 10°C скорость реакции возрастает в 2-4 раза (Правило Вант-Гоффа). При увеличении температуры от t₁ до t₂ изменение скорости реакции можно рассчитать по формуле:

		(t2 –t1) / 10
Vt2 / Vt1	= g

t₂ > t₁

(где Vt₂ и Vt₁ -–скорости реакции при температурах t₂ и t₁ соответственно; g- температурный коэффициент данной реакции).

γ = k_{(Т + 10)} / k_Т

Правило Вант-Гоффа применимо только в узком интервале температур. Более точным является уравнение Аррениуса:

k = A • e ^–Ea/RT где,

A –постоянная, зависящая от природы реагирующих веществ (предэкспоненциальный множитель);

R –универсальная газовая постоянная [8,314 Дж/(моль • К) = 0,082 л • атм/(моль • К)];

k –константа скорости реакции;

Ea –энергия активации, т.е. энергия, которой должны обладать сталкивающиеся молекулы, чтобы столкновение привело к химическому превращению.

Чем больше энергия активации Ea, тем сильнее возрастает скорость реакции при увеличении температуры.

Логарифмирование уравнения Аррениуса:

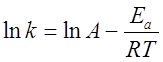или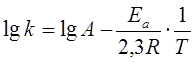

дает уравнение прямой линии. Знание констант скорости при нескольких температурах позволяет определить энергию активации данной реакции:

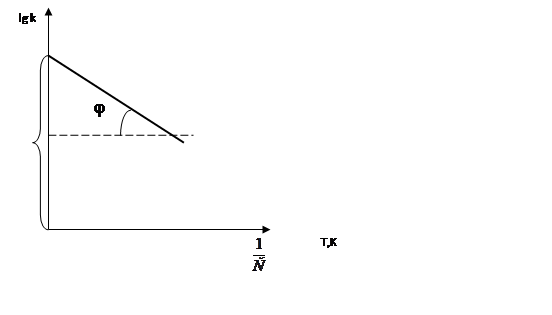
Тангенс угла наклона этой прямой к оси абсцисс равен:

.

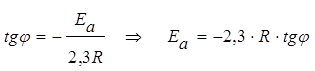Энергия активации является тем фактором, посредством которого природа реагирующих веществ влияет на скорость химической реакции.

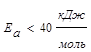- «быстрые» реакции (ионные реакции в растворах);

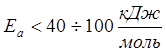- реакции с измеряемой скоростью

(Н₂SO₄ + Na₂S₂O₃ = Na₂SO₄ + SO₂ + S + H₂O);

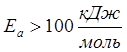- «медленные» реакции

(синтез NH₃ при обычных температурах).