Основні рівняння, що визначають питомий електричний опір в однорідному ізотропному середовищі
Розглянемо однорідне ізотропне середовище з питомим електричним опором 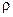 ,вякому в точці
,вякому в точці 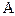 розташоване точкове джерело струму силою
розташоване точкове джерело струму силою 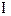 (
( 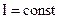 ). Інший полюс
). Інший полюс 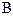 віднесений на нескінченість, і його впливом на електричне поле середовища в околі точки
віднесений на нескінченість, і його впливом на електричне поле середовища в околі точки 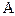 можна знехтувати (рис. 17). Необхідно визначити потенціал електричного поля в любій точці досліджуваного середовища на відстані
можна знехтувати (рис. 17). Необхідно визначити потенціал електричного поля в любій точці досліджуваного середовища на відстані 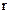 від джерела струму
від джерела струму 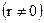 .
.
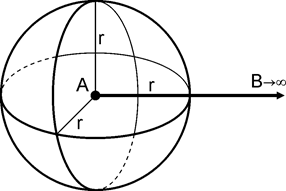
Рис. 17. До задачі визначення потенціалу електричного поля в довільній точці однорідного ізотропного середовища
Розташуємо початок координат з точкою 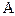 , в якій знаходиться джерело струму, та опишемо навколо неї сферу довільного радіуса
, в якій знаходиться джерело струму, та опишемо навколо неї сферу довільного радіуса 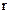 . Оскільки середовище приймається однорідним й ізотропним, то струм буде рівномірно розподіленим по поверхні сфери і, відповідно, його щільність буде дорівнювати:
. Оскільки середовище приймається однорідним й ізотропним, то струм буде рівномірно розподіленим по поверхні сфери і, відповідно, його щільність буде дорівнювати:
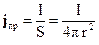 (25)
(25)
З іншого боку, згідно диференціального закону Ома, щільність струму провідності визначається:
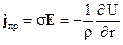 (26)
(26)
Тоді, прирівнюючи праві частини виразів (25) і (26), можна записати:
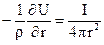 (27)
(27)
Розділивши змінні, отримаємо:
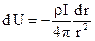 (28)
(28)
Розв’язком даного диференціального рівняння буде величина потенціалу на відстані 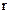 від джерела струму:
від джерела струму:
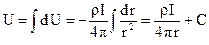 (29)
(29)
Згідно принципу регулярності потенційної функції постійна інтегрування 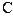 повинна бути прийнятою рівною нулеві, оскільки на нескінченості потенціал прямує до нуля.
повинна бути прийнятою рівною нулеві, оскільки на нескінченості потенціал прямує до нуля.
Звідси:
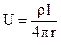 (30)
(30)
Таким чином, вираз (30) дає можливість визначити значення потенціалу електричного поля в довільній точці однорідного ізотропного середовища. Для даної моделі геометричним місцем точок, що характеризуються рівними значеннями потенціалу, буде сфера радіусу 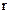 з центром у точці
з центром у точці 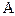 (
( 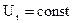 ).
).
Проведемо з точки 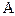 луч у довільному напрямку (див.рис. 18) та візьмемо на ньому дві точки
луч у довільному напрямку (див.рис. 18) та візьмемо на ньому дві точки 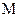 і
і 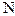 таким чином, що
таким чином, що 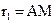 ,
, 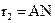 .
.
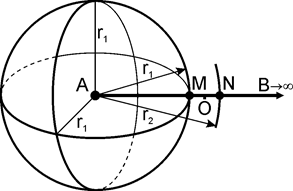
Рис. 18. До задачі визначення питомого електричного опору однорідного ізотропного середовища
Згідно виразу (30) визначимо потенціали поля в точках M і N:
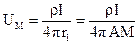 (31)
(31)
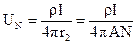 (32)
(32)
Знайдемо різницю потенціалів між точками M і N:
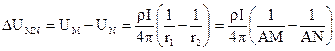 , (33)
, (33)
або
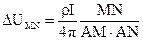 (34)
(34)
У відповідності із відомим співвідношенням, що зв’язує напруженість 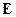 електричного поля з потенціалом U (див. вираз 26), можна встановити значення напруженості поля на відстані r від джерела струму:
електричного поля з потенціалом U (див. вираз 26), можна встановити значення напруженості поля на відстані r від джерела струму:
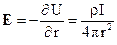 (35)
(35)
Фізичний зміст останнього виразу полягає у тому, що напруженість характеризує зміну потенціалу поля на нескінченно малому відрізку шляху (знак «мінус» вказує на зменшення величини потенціалу із віддаленням від джерела струму). Відповідно, для отримання значення напруженості електричного поля в рамках нашої моделі, необхідно відстань між точками M і N спрямувати до нуля ( 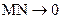 ) або, що те саме,
) або, що те саме, 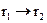 . Для нескінченно малої відстані MN можна записати:
. Для нескінченно малої відстані MN можна записати:
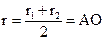 , (36)
, (36)
де AO – відстань від початку координат (точки A) до середини відрізку між нескінченно близькими точками M і N (точки O).
Отже, напруженість електричного поля у довільній точці однорідного ізотропного середовища визначиться:
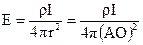 (37)
(37)
З виразів (31)-(37) отримаємо основні рівняння, що дозволяють визначити питомий електричний опір середовища:
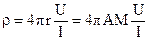 (38)
(38)
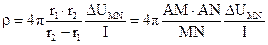 (39)
(39)
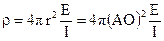 (40)
(40)
