Практический тепловой баланс

Практический тепловой баланс в общем случае определяется простым уравнением

,

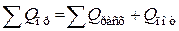где Q_пр– физическое тепло, вносимое в аппарат реагентами, материалом аппарата (для периодических процессов), тепло фазовых переходов, тепло реакции и т. д.;

Q_расх – физическое тепло, уносимое из аппарата продуктами реакции;

Q_пот – тепло, теряемое в окружающую среду.

При неизвестных размерах аппарата точное определение величин тепла, теряемого в окружающую среду, невозможно. В этом случае принимают Q_пот равным 3-5 % от максимального значения суммы вносимого или уносимого тепла. Если геометрические размеры аппарата известны, то можно оценить потери тепла по уравнению теплоотдачи

где Q – поток потерянного тепла, Вт;

F– наружная поверхность теплообмена аппарата, кв.м;

a_п – наружный коэффициент теплоотдачи, Вт/(кв.м·К);

t_п – температура наружной поверхности аппарата, °С;

t_о – температура окружающей среды, °С.

Температура наружной поверхности аппарата либо определяется из санитарных условий (<50 °С), либо задается условиями работы аппарата. Температура окружающей среды выбирается минимальной для данного помещения или района (при установке оборудования на открытом воздухе). Наружный коэффициент теплоотдачи рассчитывается по двум составляющим:

a_н = a_к + a_л,

где a_к – коэффициент теплоотдачи конвекцией;

a_л – коэффициент теплоотдачи лучеиспусканием.

Конвективный коэффициент теплоотдачи зависит от места установки оборудования и от его положения в пространстве.

Горизонтальные трубопроводы и оборудование внутри помещений: при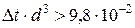

при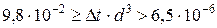

,

где d – наружный диаметр аппарата.

Для вертикальных аппаратов и трубопроводов внутри помещения:

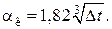
При установке оборудования на открытом воздухе:

– для плоских стенок

,

где w – скорость ветра, м/с;

l – длина стенки по направлению ветра, м;

– для аппаратов

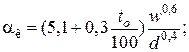
– для горизонтальных трубопроводов

Коэффициент теплоотдачи лучеиспусканием (температура в К)

,

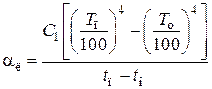где C₁ – степень черноты поверхности аппарата или трубопровода.

В случае расчета теплоизоляции аппарата или трубопровода, величина Q будет допустимой потерей тепла в окружающую среду. Тогда толщину слоя теплоизоляции можно рассчитать по формуле

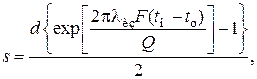
где l_из – коэффициент теплопроводности материала изоляции.

Рассмотрим расчет теплового баланса на примере.

Пример 9.2. Определить температуру реакционной смеси процесса окисления метанола до формальдегида на входе в реактор, полагая температуру на выходе из реакционной зоны равной 800 °С. Результаты материальных расчетов взять из примера 4.3. Теплоемкости компонентов реакции принять средними при температуре 650 °С.

Решение: Определим теплоемкости компонентов процесса. Из справочника [18] выпишем стандартные энтальпии образования и температурные зависимости теплоемкостей всех веществ, участвующих в процессе.

Для всех реакций процесса рассчитаем энтальпию реакции:

реакция (1) –115,9-241,84+201,2+0,5·0=-156,54 кДж/моль;

реакция (2) -115,9-0+201,2=85,3 кДж/моль;

реакция (3) -110,5-2·0+201,2=126,35 кДж/моль;

реакция (4) -74,85-241,84+201,2=-115,49 кДж/моль;

реакция (5) -376,7-241,84+115,9=-502,64 кДж/моль;

реакция (6) -393,51-241,84+115,9+1,5·0=519,45 кДж/моль.

Тогда уравнения реакций с термохимическим правилом знаков (тепловой эффект в кДж/моль) примут вид:

CH₃OH+1/2O₂=CH₂O+H₂O+156,54; (1)
CH₃OH=CH₂O+H₂-85,3; (2)
CH₃OH=CO+2H₂-126,35; (3)
CH₃OH+H₂=CH₄+H₂O+115,49; (4)
CH₃OH+O₂=HCOOH+H₂O+502,64; (5)
CH₃OH+1,5O₂=CO₂+2H₂O-519,45. (6)

На основании материального баланса рассчитаем мольный расход метанола по каждой из реакций системы, а затем и количество выделяемого или поглощаемого тепла (см. табл. 9.2.), откуда тепловой эффект процесса будет равен 604,8 кВт.

Таблица 9.1. Энтальпии образования и температурные зависимости теплоемкости

Компонент	DH0, кДж/моль	Теплоемкость, Дж/(моль·К)
a	b·103	c·106	c’·10-5
Кислород		31,46	3,30	-	-3,77
Азот		27,87	4,27	-	-
СО	-110,5	28,41	4,10	-	-0,46
СО2	-393,51	44,14	9,04	-	-8,53
Водород		27,28	3,26	-	0,502
Вода	-241,84	30,00	10,71	-	0,33
Метанол	-201,2	15,28	105,2	-31,04	-
Метан	-74,85	17,45	60,46	1,117	-
СН2О	-115,9	18,82	58,38	-15,61	-
НСООН	-376,7	19,4	112,8	-47,5	-

Таблица 9.2. К расчету суммарного теплового эффекта процесса

Номер реакции	Расход метанола, кмоль/ч	Тепло реакции, кДж/моль	Расход тепла, кВт
(1)	23,95	156,54
(2)	16,75	-85,3	-397
(3)	0,154	-126,35	5,4
(4)	0,456	115,49	-14,6
(5)	2,75	502,64	-384
(6)	2,45	-519,45
Итого:	63,93		604,8

Таблица 9.3. Средние теплоемкости компонентов реакции

Компонент	Теплоемкость, Дж/(моль·К)	Теплоемкость, Дж/(кг·К)
Кислород	31,46
Азот	27,87
СО	28,41
СО2	44,14
Водород	27,28
Вода	30,00
Метанол	15,28
Метан	17,45
СН2О	18,82
НСООН	19,40

Составим тепловой баланс процесса окисления метанола, предварительно рассчитав теплоемкости .компонентов при заданной температуре 650°С по уравнениям

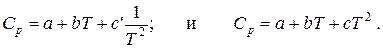
Данные расчета занесены в табл. 9.3.

Физическое тепло, вносимое компонентами в реактор:

с метанолом 1860·2,44·t/3600=1,2607·t кВт;

с кислородом 586·1,05·t/3600=0,1709·t кВт;

с азотом 1920·1,12·t/3600=0,5973·t кВт.

Всего на входе в реактор 2,0289·t кВт.

Таблица 9.4. Тепловой баланс процесса получения формальдегида

ПРИХОД ТЕПЛА	РАСХОД ТЕПЛА
Статьи	КВт	%	Статьи	КВт	%
Спирто-воздушная смесь: Метанол Кислород Азот Тепло реации Ошибки округления	650,5 88,2 308,2 604,8   0,2	39,38 5,34 18,66 36,61   0,01	Формальдегид Метанол Водяной пар НСООН СО2 СО Метан Водород Азот Потери тепла	493,4 201,7 207,7 47,8 27,1 1.1 6,6 109,9 477,9 78,7	29,87 12,21 12,57 2,89 1,64 0,07 0,40 6,65 28,93 4,77
ИТОГО:	1651,9		ИТОГО:	1651,9

Физическое тепло, уносимое компонентами из реакционной зоны:

с формальдегидом 1220·1,82·800/3600=493,4 кВт;

с метанолом 372·2,44·800/3600=201,7 кВт;

с водяным паром 572·2,13·800/3600=207,7 кВт;

с уксусной кислотой 126,5·1,7·800/3600=47,8 кВт;

с диоксидом углерода 108·1,13·800/3600=27,1 кВт;

с оксидом углерода 4,3·1,13·800/3600=1,1 кВт;

с метаном 7,3·4,05·800/3600=6,6 кВт;

с водородом 34,1·14,5·800/3600=109,9 кВт;

с азотом 1920·1,12·800/3600=477,9 кВт;

Всего на выходе – 1573,2 кВт.

Примем потери тепла в количестве 5 % от его расхода. Составим уравнение теплового баланса, из которого определим температуру на входе в реактор:

2,0289·t+604,8=1573,2+0,05·1573,2.

t=(1,051573,2-604,8)/2,0289=516 °C.

Занесем результаты расчета в табл. 9.4.

Пример 9.3.Произвести тепловой расчет и составить тепловой баланс колонны синтеза аммиака в соответствии с исходными данными:

температура в зоне реакции t=500 °C;

количество газовой смеси на входе в колонну V₁ =119025 нм³/ч;

температура газовой смеси на входе t₁=35 °С;

количество газовой смеси на выходе из колонны V₂ =102329 нм³/ч;

температура газовой смеси на выходе t₂=110 °С.

Состав газовой смеси

Компонент	Состав газовой смеси, % по объему
на входе	на выходе
Водород	74,1	62,06
Азот	24,7	20,7
Аммиак	1,2	17,24

Количество образующегося аммиака G_NH3=12500 кг/ч.

Рабочее давление в аппарате P_p=30 МПа.

Температура воды

на входе 200 °С;

на выходе 374 °С.

Решение. (Исходные данные и физико-химические свойства компонентов взяты из литературы [11, 49, 120].)

Составим уравнение теплового баланса

.

Приход тепла в колонну синтеза аммиака (SQ_пр).

1) С газовой смесью

,

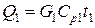где G₁ – количество поступающей газовой смеси, кмоль/ч;

С_р1 – ее мольная теплоемкость, С_р1=31,0 кДж/(кмоль×К).

Откуда 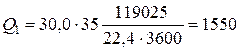кВт.

2) Тепловой эффект реакции синтеза аммиака при высоком давлении. Определяется по уравнению

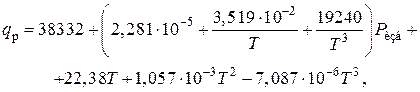
где q_p – тепловой эффект реакции, кДж/кмоль;

Р_изб – избыточное давление в реакторе, Па;

Т – температура, К.

В данном случае

Т=273+500=773 К;

Р=30×10⁶ Па.

Откуда

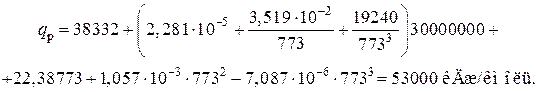
Общее количество тепла, выделяющееся при синтезе аммиака, будет

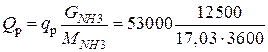=10806 кВт.

3) С охлаждающей водой на входе

,

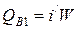где i^/ - энтальпия воды на входе при температуре 200 °С, равная 853 кДж/кг;

W – расход охлаждающей воды, кг/с.

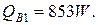
Общий приход тепла в колонну синтеза аммиака

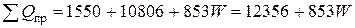кВт.

Расход тепла в колонне синтеза аммиака

1) Расход тепла, уносимого с газовым потоком, равен

,

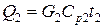где G₂ – количество уходящей газовой смеси, кмоль/ч;

С_р2 – ее мольная теплоемкость, С_р2=33,1 кДж/(кмоль×К).

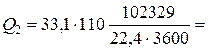4620 кВт.

2) Тепло, уносимое охлаждающей водой,

,

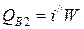где i^// - энтальпия воды на выходе при температуре 374 °С, i^//=2100 кДж/кг.

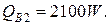
3) Потери тепла в окружающую среду можно принять равными 5 % от тепла, вносимого в колонну синтеза аммиака

кВт.

Общий расход тепла

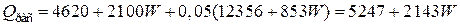кВт.

Уравнение теплового баланса

.

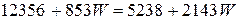Откуда расход охлаждающей воды будет равен

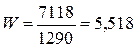кг/с.

Составим таблицу теплового баланса (табл. 9.5).

Таблица 9.5. Тепловой баланс колонны синтеза аммиака

Приход тепла	Расход тепла
Статьи прихода	кВт	Статьи расхода	кВт
Газовая смесь Реакция синтеза Охлаждающая вода		Газовая смесь Охлаждающая вода Потери тепла
Итого		Итого

Теплообмен в реакторах

При проведении реакции при постоянной температуре (изотермический процесс) степень превращения реагентов зависит от их концентрации и не зависит от температуры, поэтому уравнение материального баланса можно проинтегрировать и получить зависимость степени превращения от времени.

При неизотермическом проведении процесса (адиабатическом или программно регулируемом) приходится решать совместно уравнения материального и теплового баланса с учетом зависимости скорости реакции от температуры и, при необходимости, процесса теплопередачи.

Для создания приблизительно изотермических условий в реакторе можно применить несколько способов теплообмена:

- теплообмен при постоянной скорости теплопередачи; когда реактор обогревается топочными газами или пламенем, коэффициент теплопередачи изменяется мало, а температура настолько высока, что изменение температуры реагентов практически не влияет на температурный напор;

- теплообмен при постоянном коэффициенте теплопередачи; например, в аппаратах с мешалкой коэффициент теплопередачи зависит в основном от скорости перемешивания, которую можно держать постоянной, и скорость теплопередачи будет определяться изменением температуры реагентов;

- автоматическое регулирование скорости теплопередачи путем регулирования расхода теплоносителя или изменения температуры его фазового перехода, например за счет давления.

Последний способ, в принципе, является самым лучшим, но не всегда экономически целесообразным.

Теплообмен в реакторах смешения. Рассмотрим химическую реакцию

A+B=R+ΔH_r,

где ΔH_r – энтальпия реакции, Дж/моль.

Запишем уравнение теплового баланса, относя мольные энтальпии к некоторой температуре Т_С, например 0 ºС, являющейся уровнем отсчета.

Начальная температура реагентов Т₀, конечная – Т:

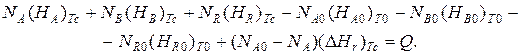
Q – количество отводимого или подводимого тепла, Дж.

Если отсутствуют фазовые превращения, то энтальпии компонентов можно выразить через теплоемкости:

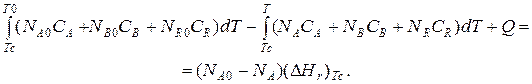
Если полагать, что теплоемкости не зависят от температуры в исследуемом интервале температур, а температура Т₀ является уровнем отсчета, то уравнение упростится:

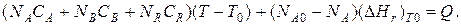
Зная состав исходной смеси, можно связать степень превращения и температуру. Для стехиометрической смеси, разделив последнее уравнение на N_A0, получим:

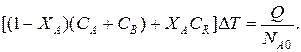
После преобразований

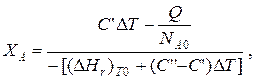
где С' и С'' – сумма теплоемкостей реагентов и продуктов реакции соответственно. Но, так как

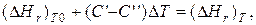
то

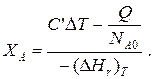
Здесь у энтальпии реакции и теплоты термодинамическое правило знаков,
т. е. тепло, подводимое к системе, считается положительным.

Для адиабатических условий Q=0, поэтому

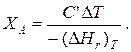
Пример 9.4. Для реакции первого порядка А+В=R, протекающей в адиабатических условиях, известны следующие данные: Т₀=28 ºС; N_A0=N_B0=1 кмоль; N_R0=0; С_А=С_В=125 Дж/(моль·К); C_R=167 Дж/(моль·К);
H= -11600 Дж/моль. Константа скорости реакции в узком интервале температур зависит линейно от температуры

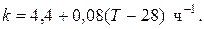
Определить степень превращения реагентов и время ее достижения, если температура в реакторе повысилась за счет реакции на 28 К?

Решение: Полагая отсутствие фазовых превращений в процессе, составим уравнение теплового баланса

[(1-X_A)(125+125)+167X_A](T - 28)-11600X_A=0;

(250-83X_A)(T-28)=11600X_A;

T-28=28=11600X_A/(250-83X_A);

X_A=0,503.

Определим время реакции из баланса массы при условии реакции первого порядка

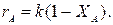
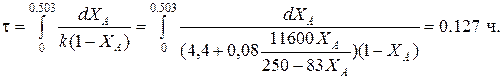
(Последний интеграл вычислен численным методом по формуле Симпсона.)

Составим тепловой баланс в дифференциальной форме, полагая, что за элементарное время dt скорость реакции r_A и скорость теплопередачи R определяются уравнениями

;

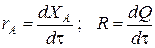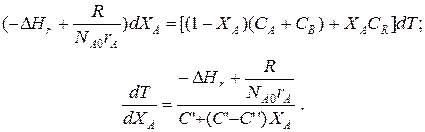
Теплоемкость и скорость реакции являются известными функциями температуры. Если скорость теплопередачи задана в функции от температуры, то последнее уравнение можно проинтегрировать. Для трех рассмотренных способов теплообмена связь между температурой и скоростью теплопередачи имеет вид:

- теплообмен при постоянной скорости теплопередачи

R=const;

- теплообмен при постоянном коэффициенте теплопередачи

R=KS(T_т-T), KS=const, T_т=const;

- автоматическое регулирование скорости теплопередачи

R=DH_r·r_A=KS(T_т-T), T=const.

Здесь: K – коэффициент теплопередачи, Вт/(м²*К);

S – поверхность теплопередачи, м²;

T_т – температура теплоносителя.

Пример 9.5. Для реакции первого порядка известны следующие данные: энтальпия реакции DH_r=11600Дж/моль; константа скорости реакции k=0,8 ч^-1; коэффициент теплопередачи К=51 Вт/(м²·К); начальная загрузка реагента N_A0=2270 моль. Определить поверхность теплообмена, необходимую для поддержания постоянной температуры t=49 ºС до конечной степени превращения X_A=70 %. Нагрев осуществляется паром, температуру которого Т_т можно регулировать в пределах от 110 до 177 ºС.

Решение: Скорость подвода тепла должна быть наибольшей в начале процесса, когда Х_А=0, а скорость реакции – наибольшая. Расчет будем производить, используя уравнение

DH_r·r_A=KS₁(T_т-T).

Откуда максимальная поверхность теплопередачи в этот момент выразится уравнением

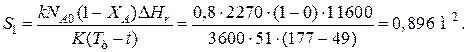
При такой поверхности и конечной степени превращения Х_А=0.7 температура теплоносителя должна быть равна

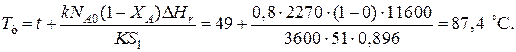
Эту температуру не обеспечить паром заданных параметров. Степень превращения, отвечающая наиболее низкой заданной температуре теплоносителя 110 ºС, при поверхности теплопередачи S₁ составит

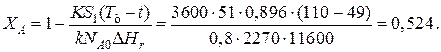
При температуре теплоносителя 110 ºС и степени превращения 0,7 имеем

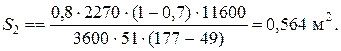
При Х_А=0.524 и S₂=0.564 м² имеем

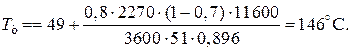
Таким образом, нагреватель должен состоять из двух параллельных змеевиков, один из которых с поверхностью S₁=0,564 м², а другой –
S₂=0,896-0,564=0,332 м². При снижении температуры пара до 110 ºС змеевик с поверхностью 0,332 м² следует отключить.

Кривые регулирования строятся по уравнениям

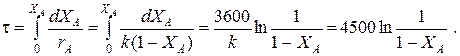
При Х_А£0.52 Т_Т=49+128(1-Х_А);

при Х_А>0.52 Т_Т=49+203(1-Х_А).

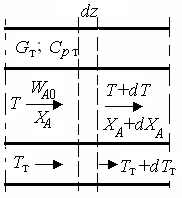Рис. 9.2. К расчету теплообмена в реакторе вытеснения

Теплообмен в реакторах вытеснения. Если полагать отсутствие в реакционной зоне реактора идеального вытеснения радиальных градиентов температур, то можно составить три уравнения, одно из которых – баланс массы, второе – баланс тепла по реакционной массе и третье – баланс тепла по теплоносителю. Схема тепло- и массообмена в элементе реактора представлена на рис. 9.2.

Уравнение баланса массы

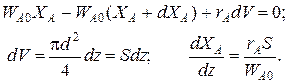
Уравнение баланса тепла в элементе реакционной зоны

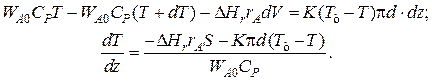
Уравнение баланса тепла в элементе рубашки

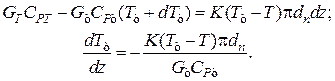
Совместное решение системы из трех дифференциальных уравнений дает возможность определить распределение степеней превращения, температур реакционной смеси и теплоносителя по длине реактора идеального вытеснения.

Для адиабатического реактора идеального вытеснения получаем систему из двух дифференциальных уравнений

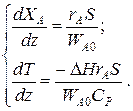
Пример 9.6. В гомогенном реакторе идеального вытеснения, представляющем собой трубу внутренним диаметром 50мм, протекает адиабатическая реакция второго порядка. Кинетические параметры реакции: энергия активации Е=58200 Дж/моль, k₀=2·10⁷ м³/(моль·ч). Начальная концентрация реагента 20 кмоль/м³, его мольный расход 60 кмоль/ч, теплоемкость реакционной смеси 125 Дж/(моль·К). Энтальпия реакции
DH_r=-10000 Дж/моль. Определить длину реактора при 90 %-ной степени превращения, если начальная температура реагентов 77 ºС.

Решение: Подставим исходные данные в систему дифференциальных уравнений материального и теплового баланса адиабатического реактора:

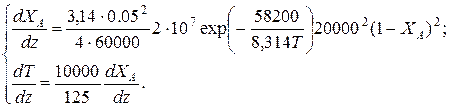
После преобразований получим:

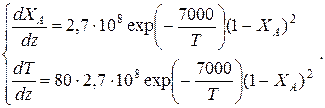
Таблица 9.6.Результаты решения дифференциального уравнения

z, м	0,0	0,2	0,4	0,6	0,8	1,0	1,2	1,3
XA, %	0,00	12,94	30,31	51,50	70,54	82,22	88,32	90,21
T, K	350,0	360,4	372,2	391,2	406,4	415,8	420,7	422,2

Решая полученную систему численным методом, можем найти длину реактора. Например, при решении модифицированным методом Эйлера при шаге интегрирования 0.02 м получаем длину реактора 1,3 м (см.
табл. 9.6).